江苏省扬州市仪征市2022-2023学年七年级下学期期中数学试题

试卷更新日期：2023-06-08 类型：期中考试

进入出卷网下载

一、单选题

1. 如图，在上网课时把平板放在三角形支架上用到的数学道理是（）

A、三角形的稳定性 B、对顶角相等 C、垂线段最短 D、两点之间线段最短

查看试题解析
2. 下列式子运算正确的是（）

A、x⁵÷x⁵＝0 B、x²•x³＝x⁶ C、（2x）²＝4x² D、（x³）⁴＝x⁷

查看试题解析
3. 若代数式x²-4x+a可化为（x-b）²-1，则a+b是（）

A、5 B、4 C、3 D、2

查看试题解析
4. 如图，将木条a，b与c钉在一起，∠1＝100°，∠2＝60°．要使木条a与b平行，木条a顺时针旋转的度数至少是（）

A、10° B、20° C、30° D、40°

查看试题解析
5. 如图，已知直线AB//CD，BE平分∠ABC，交CD于D，∠CDE=150°，则∠C的度数为（）．

A、150° B、130° C、120° D、100°

查看试题解析
6. 式子 $5^{5} + 5^{5} + 5^{5} + 5^{5} + 5^{5}$ 化简的结果是（）

A、 $5^{2}$ B、 $5^{5}$ C、 $5^{6}$ D、 $5 + 5^{5}$

查看试题解析
7. 我国古代数学名著《孙子算经》中记载了一道题，大意是：求100匹马恰好拉了100片瓦，已知1匹大马能拉3片瓦，3匹小马能拉1片瓦，问有多少匹大马、多少匹小马？若设大马有x匹，小马有y匹，那么可列方程组为（　　）

A、 $\{\begin{matrix} x + y = 100 \\ 3 x + 3 y = 100 \end{matrix}$ B、 $\{\begin{matrix} x + y = 100 \\ x + 3 y = 100 \end{matrix}$ C、 $\{\begin{matrix} x + y = 100 \\ 3 x + \frac{1}{3} y = 100 \end{matrix}$ D、 $\{\begin{matrix} x + y = 100 \\ 3 x + y = 100 \end{matrix}$

查看试题解析
8. 从前，古希腊一位庄园主把一块边长为 $a$ 米（ $a > 6$ ）的正方形土地租给租户张老汉.第二年，他对张老汉说：“我把这块地的一边增加6米，相邻的另一边减少6米，变成矩形土地继续租给你，租金不变，你也没有吃亏，你看如何？”如果这样，你觉得张老汉的租地面积会（）

A、没有变化 B、变大了 C、变小了 D、无法确定

查看试题解析

二、填空题

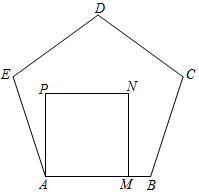
9. 碳纳米管的硬度与金刚石相当，却拥有良好的柔软性，我国某物理研究组已研制出直径为0.00000000052米的碳纳米管，将0.00000000052用科学记数法表示为．

查看试题解析
10. 一个多边形的内角和等于900°，则它的边数是 .

查看试题解析
11. 已知xy＝2，x+y＝3，则x²y+xy²＝．

查看试题解析
12. 若x²+ax+4是完全平方式，则a= ．

查看试题解析
13. 若 $a^{m} = 3$ ， $a^{n} = 7$ ，则 $a^{m + n}$ =.

查看试题解析
14. 如图，正方形 $A M N P$ 的边 $A M$ 在正五边形 $A B C D E$ 的边 $A B$ 上，则 $∠ P A E =$ $°$ ．

查看试题解析
15. 如图，AD 是△ABC 的中线，BE 是△ABD 的中线， EF ⊥ BC 于点 F.若 $S_{△ A B C} = 24$ ， BD = 4 ，则 EF 长为.

查看试题解析
16. 若方程组 ${\begin{array}{l} x - 2 m = 3 \\ 2 + y = m \end{array}$ ，则у= ．（用含x的代数式表示）

查看试题解析
17. 整式mx+n的值随x的取值不同而不同，下表是当x取不同值时对应的整式的值：则关于x的方程﹣mx+n=8的解为．
x
-2
-1
0
1
2
mx+n
7
5
3
1
-1

查看试题解析
18. 定义一种新运算 $\int_{b}^{a} n x^{n - 1} d x = a^{n} - b^{n}$ ，例如 $\int_{m}^{k} 2 x d x = k^{2} - m^{2}$ ．若 $\int_{2}^{k} - x^{2} d x = - \frac{1}{4}$ ，则 $k =$ ．

查看试题解析

三、解答题

19. 计算

(1)、 $(- 1)^{0} - {(- \frac{1}{3})}^{- 2} + 4 \times 2^{- 1}$ ；

(2)、 $(2 a + b) (b - 2 a) - (a - 3 b)^{2}$ ．

查看试题解析
20. 分解因式：

(1)、2x²﹣4xy+2y²

(2)、m²（m﹣n）+（n﹣m）

查看试题解析
21. 解方程组：

(1)、 ${\begin{array}{l} 3 x + 2 y = 14 \\ x = y + 3 \end{array}$ ；

(2)、 ${\begin{array}{l} \frac{x}{3} - \frac{y}{4} = 1 \\ 3 x - 4 y = 2 \end{array}$ ．

查看试题解析
22. 在正方形网格中，每个小正方形的边长均为1个单位长度，△ABC的三个顶点的位置如图所示．

(1)、该三角形的面积是；

(2)、仅用无刻度的直尺完成作图：作出△ABC的高AH

查看试题解析
23. 下图是东东同学完成的一道作业题，请你参考东东的方法解答下列问题．
东东的作业
计算： $4^{5} \times {(- 0.25)}^{5}$ ；
解：原式 $= {(- 4 \times 0.25)}^{5} = {(- 1)}^{5} = - 1$

(1)、计算：
① $8^{2022} \times {(- 0.125)}^{2022}$ ；
② ${(\frac{12}{5})}^{11} \times {(\frac{5}{6})}^{13} \times {(\frac{1}{2})}^{12}$ ；

(2)、若 $3 \times 9^{n} \times 8 1^{n} = 3^{25}$ ，请求出 $n$ 的值．

查看试题解析
24. 如图，△ABC中，E是AB上一点，过D作DE $∥$ BC交AB于E点，F是BC上一点，连接DF.若∠AED=∠1.

(1)、求证：AB $∥$ DF.

(2)、若∠1=52°，DF平分∠CDE，求∠C的度数.

查看试题解析
25. 已知 ${\begin{cases} x = 3 \\ y = 1 \end{cases}$ 是方程2x-ay=9的一个解，解决下列问题：

(1)、求 $a$ 的值；

(2)、化简并求值： $(a - 1) (a + 1) - 2 {(a - 1)}^{2} + a (a - 3)$

查看试题解析
26. 找规律：观察算式
$1^{3} = 1$
$1^{3} + 2^{3} = 9$
$1^{3} + 2^{3} + 3^{3} = 36$
$1^{3} + 2^{3} + 3^{3} + 4^{3} = 100$
…

(1)、按规律填空
$1^{3} + 2^{3} + 3^{3} + 4^{3} + ⋯ + 1 0^{3} =$ ；
$1^{3} + 2^{3} + 3^{3} + 4^{3} + ⋯ + n^{3} =$ ．

(2)、由上面的规律计算： $1 1^{3} + 1 2^{3} + 1 3^{3} + 1 4^{3} + ⋯ + 5 0^{3} =$ （要求：写出计算过程）

查看试题解析
27. 如图，△ABC中，∠ACB=90°，点D、E分别在边AC、AB上运动（不与顶点重合），点F在线段CD上（不与点D、C重合），射线ED与射线BF相交于点G．

(1)、如图1，若DE $∥$ BC，∠EDB=2∠G，说明：BG平分∠DBC．

(2)、如图2，若∠EDB=m∠ADB，∠DBG=n∠DBC，∠G=45°．
①若m= $\frac{5}{12}$ ， n= $\frac{1}{6}$ ，求∠DBC的值．
②若n= $\frac{1}{2}$ ，求m的值．
③若3m-n=1且m≠ $\frac{1}{2}$ ，求∠DBC的度数．

查看试题解析
28. 已知一个各个数位上的数字均不为0的四位正整数 $M = \bar{a b c d} (a > c)$ ，以它的百位数字作为十位，个位数字作为个位，组成一个新的两位数s，若s等于M的千位数字与十位数字的平方差，则称这个数M为“平方差数”，将它的百位数字和千位数字组成两位数 $\bar{b a}$ ，个位数字和十位数字组成两位数 $\bar{d c}$ ，并记 $T (M) = \bar{b a} + \bar{d c}$ ．
例如：6237是“平方差数”，因为 $6^{2} - 3^{2} = 27$ ，所以6237是“平方差数”；
此时 $T (6237) = 26 + 73 = 99$ ．
又如：5135不是“平方差数”，因为 $5^{2} - 3^{2} = 16 \neq 15$ ，所以5135不是“平方差数”．

(1)、判断7425是否是“平方差数”？并说明理由；

(2)、若 $M = \bar{a b c d}$ 是“平方差数”，且 $T (M)$ 比M的个位数字的9倍大30，求所有满足条件的“平方差数”M．

查看试题解析

x	-2	-1	0	1	2
mx+n	7	5	3	1	-1