江苏省盐城市盐都区2022-2023学年八年级下学期期中数学试题

试卷更新日期：2023-06-08 类型：期中考试

进入出卷网下载

一、单选题

1. 下列选项中的图形是理想、蔚来、小鹏、哪吒四款新能源汽车的标志，其中是中心对称图形的为（）

A、 B、 C、 D、

查看试题解析
2. 要使分式 $\frac{1}{x - 1}$ 有意义，则x的取值范围是（）

A、 $x \neq 0$ B、 $x < 1$ C、 $x \neq 1$ D、 $x > 1$

查看试题解析
3. 下列调查中，适合用普查的是（）

A、对旅客上飞机前的安检 B、调查全中国中学生的近视率 C、调查某品牌电视机的使用寿命 D、调查长江中现有鱼的种类

查看试题解析
4. 菱形具有而矩形不一定具有的性质是（　　）

A、内角和等于360° B、对角相等 C、对边平行且相等 D、对角线互相垂直

查看试题解析
5. 如果把分式 $\frac{x^{2}}{x + y}$ 中x、y的值都变为原来的2倍，则分式的值（）

A、变为原来的2倍 B、不变 C、变为原来的 $\frac{1}{2}$ D、变为原来的4倍

查看试题解析
6. 如图，在 $△ A B C$ 中，D，E，F分别是 $B C$ ， $A C$ ， $A B$ 的中点．若 $A B = 4$ ， $B C = 6$ ，则四边形 $B D E F$ 的周长是（）

A、8 B、10 C、12 D、16

查看试题解析
7. 如图，在平行四边形 $A B C D$ 中， $∠ A B C$ 的平分线交 $A D$ 于点B， $∠ B C D$ 的平分线交 $A D$ 于点F，若 $A B = 3$ ， $A D = 4$ ，则 $E F$ 的长是（）

A、0.5 B、1 C、1.5 D、2

查看试题解析
8. 如图，矩形 $A B C D$ 中，连接 $B D$ ，分别以B、D为圆心，大于 $\frac{1}{2} B D$ 的长为半径画弧，两弧交于P、Q两点，作直线 $P Q$ ，分别与 $A D$ 、 $B C$ 交于点M、N，连接 $B M$ 、 $D M$ ．若 $A D = 9$ ， $A B = 3$ ．则四边形 $M B N D$ 的周长为（）

A、24 B、20 C、16 D、12

查看试题解析

二、填空题

9. 某实验学校为了解七年级1200名学生体质健康情况，从中抽取了100名学生进行测试，在这个问题中，样本容量是．

查看试题解析
10. 当 $x =$ 时，分式 $\frac{x - 2}{x - 1}$ 的值为0．

查看试题解析
11. 某医院病房护土对一位病人每小时测一次体温，要把这位病人一昼夜体温变化情况用统计图表示出来选用统计图比较合适（填“条形”、“扇形”、“折线”）．

查看试题解析
12. 若 $\frac{a}{b} = \frac{1}{2}$ ，则分式 $\frac{3 a + b}{b} =$ ．

查看试题解析
13. 若一个菱形的边长为10 $c m$ ，一条对角线长为16 $c m$ ，则该菱形的面积为 $c m^{2}$ ．

查看试题解析
14. 如图，四边形ABCD中，E，F，G，H分别是边AB、BC、CD、DA的中点．若四边形EFGH为菱形，则对角线AC、BD应满足条件．

查看试题解析
15. 如图，正方形 $A B C D$ 的边长为10，点 $E$ 是 $C D$ 的中点， $H G$ 垂直平分 $A E$ 且分别交 $A E$ 、 $B C$ 于点 $H$ 、 $G$ ，则 $B G =$ ．

查看试题解析
16. 如图，在矩形 $A B C D$ 中， $A B = 3$ ， $B C = 4$ ， E、F为 $A B$ 、 $B C$ 边上的动点，以 $E F$ 为斜边作等腰直角 $△ G E F$ （其中 $E G = F G$ ， $∠ E G F = 90 °$ ），连接 $C G$ 、 $D G$ ，则 $C G + D G$ 的最小值为．

查看试题解析

三、解答题

17. 计算：

(1)、 $\frac{3 x + 2}{x - 1} - \frac{5}{x - 1}$ ；

(2)、 $\frac{m^{2}}{m^{2 -} 4} \div \frac{m}{m + 2}$ ．

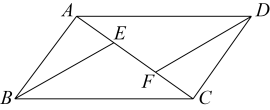
查看试题解析
18. 先化简，再求值： $(1 - \frac{3}{x + 1}) \div \frac{x^{2} - 4 x + 4}{x^{2} - 1}$ ；其中x的值从 $- 1$ 、0、1、2中选取．

查看试题解析
19. 已知：如图 E、F 是平行四边形 ABCD 的对角线 AC 上的两点，AF＝CE．求证：BE=DF．

查看试题解析
20. 已知四边形 $A B C D$ 为矩形.点E是边 $A D$ 的中点.请仅用无刻度的直尺完成下列作图，不写作法，保留作图痕迹.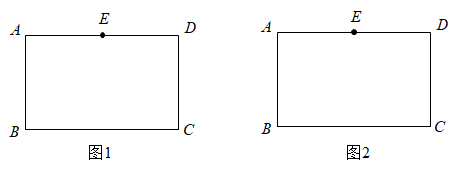

(1)、在图1中作出矩形 $A B C D$ 的对称轴m，使 $m ∥ A B$ ；

(2)、在图2中作出矩形 $A B C D$ 的对称轴n：使 $n ∥ A D$ .

查看试题解析
21. 在一个不透明的盒子里装有黑、白两种颜色的球共20只，这些球除颜色外其余完全相同.搅匀后，小明做摸球实验，他从盒子里随机摸出一只球记下颜色后，再把球放回盒子中，不断重复上述过程，下表是实验中的一组统计数据.
摸球的次数n
100
200
300
500
800
1000
3000
摸到白球的次数m
52
138
178
302
481
599
1803
摸到白球的频率
0.52
0.69
0.593
0.604
0.60
0.599
0.601

(1)、若从盒子里随机摸出一只球，则摸到白球的概率的估计值为；(精确到0.1)

(2)、盒子里白色的球有只；

(3)、若将m个完全一样的白球放入这个盒子里并摇匀，随机摸出1个球是白球的概率是0.8，求m的值.

查看试题解析
22. 某校举办了“学党史、知党恩、跟党走”手抄报设计大赛，从八年级学生中随机抽取部分学生进行问卷调查，要求每名学生从4个获奖作品中选择一个自己最喜欢的作品，根据调查结果绘制成如图所示的两幅不完整的统计图．请你根据图中信息解答下列问题：

(1)、参加此次问卷调查的学生人数是；

(2)、在扇形统计图中，选择“作品1”的学生所对应扇形的圆心角的度数是；

(3)、将条形统计图补充完整：

(4)、若该校八年级学生共有450名，请估计八年级学生中选择“作品3”的人数．

查看试题解析
23. 如图，线段DE与AF分别为△ABC的中位线与中线.

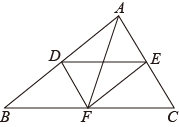(1)、求证：AF与DE互相平分；

(2)、当线段AF与BC满足怎样的数量关系时，四边形ADFE为矩形？请说明理由.

查看试题解析
24. 如图，在矩形纸片 $A B C D$ 中， $A B = 4 ， B C = 3$ ，将矩形纸片 $A B C D$ 折叠，使点C与点A重合，点B落在点G处，折痕为 $E F$ ．

(1)、连接 $C E$ ，试判断四边形 $A E C F$ 的形状并说明理由；

(2)、求折痕 $E F$ 的长．

查看试题解析
25. 阅读下列材料：我们知道，分子比分母小的数叫做“真分数”：分子比分母大，或者分子、分母同样大的分数，叫做“假分数”．类似地，我们定义：在分式中，对于只含有一个字母的分式，当分子的次数大于或等于分母的次数时，我们称之为“假分式”：当分子的次数小于分母的次数时，我们称之为“真分式”．
如： $\frac{x - 1}{x + 1}$ ， $\frac{x^{2}}{x - 1}$ 这样的分式就是假分式；再如： $\frac{3}{x + 1}$ ， $\frac{2 x}{x^{2} + 1}$ 这样的分式就是真分式，假分数 $\frac{7}{4}$ 可以化成 $1 + \frac{3}{4}$ （即 $1 \frac{3}{4}$ ）带分数的形式，类似的，假分式也可以化为带分式．如： $\frac{x - 1}{x + 1} = \frac{(x + 1) - 2}{x + 1} = 1 - \frac{2}{x + 1}$ ．
解决下列问题：

(1)、分式 $\frac{5}{x}$ 是（填“真分式”或“假分式”）；假分式 $\frac{x + 5}{x + 2}$ 可化为带分式形式；

(2)、如果分式 $\frac{x - 4}{x - 1}$ 的值为整数，求满足条件的整数x的值；

(3)、若分式 $\frac{3 x^{2} + 8}{x^{2} + 2}$ 的值为m，则m的取值范围是（直接写出结果）

查看试题解析
26. 综合与实践课上，老师让同学们以“正方形的折叠”为主题开展数学活动．
操作
操作一：对折正方形纸片 $A B C D$ ，使 $A D$ 与 $B C$ 重合，得到折痕 $E F$ ，把纸片展平；

操作二：在 $A D$ 上选一点P，沿 $B P$ 折叠，使点A落在正方形内部点M处，把纸片展平，连接 $P M$ ， $B M$ ，延长 $P M$ 交 $C D$ 于点Q，连接 $B Q$ （如图1）．

(1)、探究
① 特例研究

按（1）中操作，当点M在 $E F$ 上时（如图2）， $∠ A B M =$ $°$ ， $∠ P B Q =$ $°$ ；

② 一般推演

改变点P在 $A D$ 上的位置（点P不与点A，D重合）进行（1）中操作．随着点P的位置改变， $∠ P B Q$ 的度数是否发生变化，若不变，请按图3所示求出 $∠ P B Q$ 的度数，若变化，说明理由；

(2)、应用
在（2）的探究中，已知正方形纸片 $A B C D$ 的边长为6 $c m$ ，当 $F Q = 1$ $c m$ 时，直接写出 $A P$ 的长；

(3)、拓展
在（2）的探究中，连接 $A C$ 分别交 $B P 、 B Q$ 于点G、H（如图4），请直接写出线段 $A G$ 、 $G H$ 、 $C H$ 之间一个等量关系式．

查看试题解析

摸球的次数n	100	200	300	500	800	1000	3000
摸到白球的次数m	52	138	178	302	481	599	1803
摸到白球的频率	0.52	0.69	0.593	0.604	0.60	0.599	0.601