江苏省无锡市锡山区2022-2023学年九年级下学期期中数学试题
试卷更新日期:2023-06-08 类型:期中考试
一、单选题
-
1. 的相反数是( )A、 B、 C、 D、2. 要使二次根式 有意义,则x的取值可以是( )A、0 B、1 C、2 D、43. 下列各式中,计算正确的是( )A、 B、 C、x3÷x2=x D、(x3)2=x94. 下列图形中,既是轴对称图形,又是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 5. 下列调查中,最适合采用普查的是( )A、检测神舟十五号飞船的零部件 B、调查无锡市中学生的视力状况 C、调查江苏省中学生的体育运动情况 D、调查一批节能灯的使用寿命6. 《九章算术》是中国古代的一本重要数学著作,其中有一道方程的应用题:“五只雀、六只燕共重16两,雀重燕轻.互换其中一只,恰好一样重.假设每只雀的重量相同,每只燕的重量相同,问每只雀、燕的重量各为多少?”解:设雀每只两,燕每只两,则可列出方程组为( )A、 B、 C、 D、7. 已知:在△ABC中,AC=BC,点D、E分别是边AB、AC的中点,延长DE至点F,使得EF=DE,那么四边形AFCD一定是( )A、菱形 B、矩形 C、直角梯形 D、等腰梯形8. 如图,在平面直角坐标系中,直线与y轴交于点C,与反比例函数 , 在第一象限内的图像交于点B,连接 , 若 , , 则m的值是( )
5. 下列调查中,最适合采用普查的是( )A、检测神舟十五号飞船的零部件 B、调查无锡市中学生的视力状况 C、调查江苏省中学生的体育运动情况 D、调查一批节能灯的使用寿命6. 《九章算术》是中国古代的一本重要数学著作,其中有一道方程的应用题:“五只雀、六只燕共重16两,雀重燕轻.互换其中一只,恰好一样重.假设每只雀的重量相同,每只燕的重量相同,问每只雀、燕的重量各为多少?”解:设雀每只两,燕每只两,则可列出方程组为( )A、 B、 C、 D、7. 已知:在△ABC中,AC=BC,点D、E分别是边AB、AC的中点,延长DE至点F,使得EF=DE,那么四边形AFCD一定是( )A、菱形 B、矩形 C、直角梯形 D、等腰梯形8. 如图,在平面直角坐标系中,直线与y轴交于点C,与反比例函数 , 在第一象限内的图像交于点B,连接 , 若 , , 则m的值是( )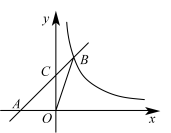 A、6 B、8 C、10 D、129. 如图1,点E为矩形的边上一点,动点P,Q同时从点B出发以相同的速度运动,其中,点P沿折线--运动到点C时停止,点Q沿运动到点C时停止.设点P出发xs时,的面积为ycm2 , y与x的函数关系如图2所示(曲线为抛物线的一部分),则下列结论中正确的有( )
A、6 B、8 C、10 D、129. 如图1,点E为矩形的边上一点,动点P,Q同时从点B出发以相同的速度运动,其中,点P沿折线--运动到点C时停止,点Q沿运动到点C时停止.设点P出发xs时,的面积为ycm2 , y与x的函数关系如图2所示(曲线为抛物线的一部分),则下列结论中正确的有( )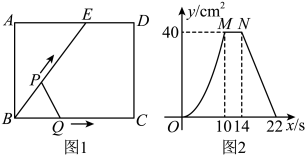
①;②P,Q的运动速度都是2cm/s;③cm;④当时, .
A、①③ B、①④ C、①②④ D、②③④10. 已知在平行四边形中, , , 点E在上, , 将沿翻折到 , 连接 , 则的长为( )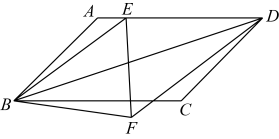 A、 B、 C、 D、4
A、 B、 C、 D、4二、填空题
-
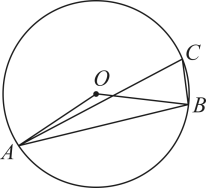
11. 中国空间站飞行的圆形轨道周长约为43000000米,把43000000用科学记数法表示为.12. 分解因式: .13. 已知圆锥的底面半径为3cm,母线长为5cm,则圆锥的侧面是cm2 .14. 如图,A、B、C为上三点,若 , 则度数为°.
 15. 如图,利用标杆测量楼高,点A,D,B在同一直线上, , , 垂足分别为E,C.若测得 , , , 则楼高m.
15. 如图,利用标杆测量楼高,点A,D,B在同一直线上, , , 垂足分别为E,C.若测得 , , , 则楼高m.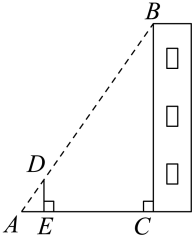 16. 等边△ABC中,点D在射线CA上,且AB=2AD,则tan∠DBC的值为17. 将二次函数的图像向上平移a个单位长度,当抛物线经过点时,a的值为;当抛物线与两坐标轴有且只有2个公共点时,a的值为 .18. 如图,在中, , 点是边上的一动点.已知 , 现将绕点按逆时针方向旋转,点是边的中点,则 , 长度的最小值为 .
16. 等边△ABC中,点D在射线CA上,且AB=2AD,则tan∠DBC的值为17. 将二次函数的图像向上平移a个单位长度,当抛物线经过点时,a的值为;当抛物线与两坐标轴有且只有2个公共点时,a的值为 .18. 如图,在中, , 点是边上的一动点.已知 , 现将绕点按逆时针方向旋转,点是边的中点,则 , 长度的最小值为 .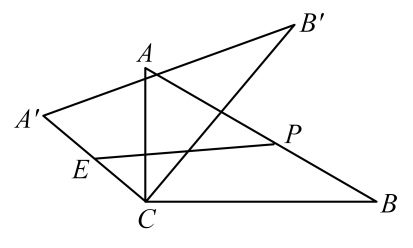
三、解答题
-
19. 按要求解答下列各题:(1)、计算:;(2)、化简: .20.(1)、解方程:;(2)、解不等式组: .21. 已知:如图,在中,E是的中点,点F在上, , 交的延长线于点D.
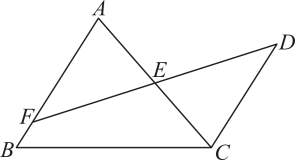 (1)、求证:;(2)、若 , 求的长.22. 为了继续宣传新冠疫苗接种的重要性,某小区物业部门准备在已经接种疫苗的居民中招募2名志愿宣传者,现有2名男性2名女性共4名居民报名.(1)、从4人中抽取1人为男性的概率是;(2)、请用列表或画树状图的方法,求要从这4人中随机挑选2人,恰好抽到一名男性和一名女性的概率.23. 实验学校想了解学生家长对“双减”政策的认知情况,随机抽查了部分学生家长进行调查,将抽查的数据结果进行统计,并绘制两幅不完整的统计图(A:不太了解,B:基本了解,C:比较了解,D:非常了解).请根据图中提供的信息回答以下问题:
(1)、求证:;(2)、若 , 求的长.22. 为了继续宣传新冠疫苗接种的重要性,某小区物业部门准备在已经接种疫苗的居民中招募2名志愿宣传者,现有2名男性2名女性共4名居民报名.(1)、从4人中抽取1人为男性的概率是;(2)、请用列表或画树状图的方法,求要从这4人中随机挑选2人,恰好抽到一名男性和一名女性的概率.23. 实验学校想了解学生家长对“双减”政策的认知情况,随机抽查了部分学生家长进行调查,将抽查的数据结果进行统计,并绘制两幅不完整的统计图(A:不太了解,B:基本了解,C:比较了解,D:非常了解).请根据图中提供的信息回答以下问题: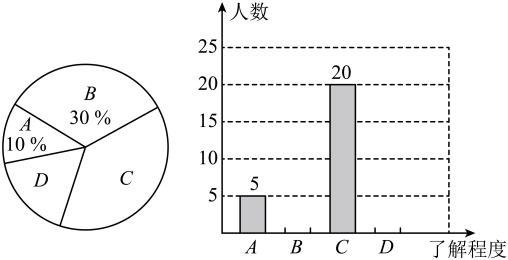 (1)、请求出这次被调查的学生家长共有多少人?(2)、请补全条形统计图.(3)、试求出扇形统计图中“比较了解”部分所对应的圆心角度数.(4)、该学校共有2400名学生家长,估计对“双减”政策了解程度为“非常了解”的学生家长大约有多少?24. 如图,已知中, , 请用直尺(不带刻度)和圆规,按下列要求作图(不要求写作法,但要保留作图痕迹).
(1)、请求出这次被调查的学生家长共有多少人?(2)、请补全条形统计图.(3)、试求出扇形统计图中“比较了解”部分所对应的圆心角度数.(4)、该学校共有2400名学生家长,估计对“双减”政策了解程度为“非常了解”的学生家长大约有多少?24. 如图,已知中, , 请用直尺(不带刻度)和圆规,按下列要求作图(不要求写作法,但要保留作图痕迹).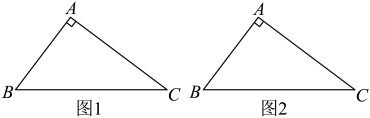 (1)、在图1中,求作点D,使四边形为平行四边形;(2)、在图2中,求作菱形 , 使菱形的顶点D落在边上;(3)、在(2)的条件下,若 , 则菱形周长为 .25. 如图,为的内接三角形, , 垂足为D,直径平分 , 交于点F,连结 .
(1)、在图1中,求作点D,使四边形为平行四边形;(2)、在图2中,求作菱形 , 使菱形的顶点D落在边上;(3)、在(2)的条件下,若 , 则菱形周长为 .25. 如图,为的内接三角形, , 垂足为D,直径平分 , 交于点F,连结 .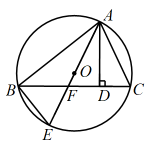 (1)、求证:;(2)、若 , 求的长;26. 某体育用品店计划购进篮球、排球共200个进行销售,所用资金不超过5000元.已知篮球、排球的进价分别为每个30元、24元,每只篮球售价是每只排球售价的1.5倍,某学校在该店用1800元购买的篮球数比用1500元购买的排球数少10个.(1)、求篮球、排球的售价分别为每个多少元?(2)、该店为了让利于消费者,决定篮球的售价每个降价3元,排球的售价每个降价2元,问该店应如何进货才能获得最大利润?(购进的篮球、排球全部销售完.)27. 如图,在矩形中, , , P是线段边上的任意一点(不含端点A、D),连接 , 过点P作交于E.
(1)、求证:;(2)、若 , 求的长;26. 某体育用品店计划购进篮球、排球共200个进行销售,所用资金不超过5000元.已知篮球、排球的进价分别为每个30元、24元,每只篮球售价是每只排球售价的1.5倍,某学校在该店用1800元购买的篮球数比用1500元购买的排球数少10个.(1)、求篮球、排球的售价分别为每个多少元?(2)、该店为了让利于消费者,决定篮球的售价每个降价3元,排球的售价每个降价2元,问该店应如何进货才能获得最大利润?(购进的篮球、排球全部销售完.)27. 如图,在矩形中, , , P是线段边上的任意一点(不含端点A、D),连接 , 过点P作交于E.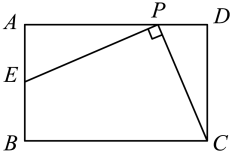 (1)、若 , 则;(2)、当点P在上运动时,对应的点E也随之在上运动,求的取值范围;(3)、在线段上是否存在不同于P的点Q,使得?若存在,求线段与之间的数量关系;若不存在,请说明理由.28. 抛物线与x轴交于 , B两点(点A在点B的左侧),交y轴正半轴于点C,且 .(1)、如图1,已知 .
(1)、若 , 则;(2)、当点P在上运动时,对应的点E也随之在上运动,求的取值范围;(3)、在线段上是否存在不同于P的点Q,使得?若存在,求线段与之间的数量关系;若不存在,请说明理由.28. 抛物线与x轴交于 , B两点(点A在点B的左侧),交y轴正半轴于点C,且 .(1)、如图1,已知 .①请直接写出a,b,c的值;
②连接、 , P为上方抛物线上的一点,连接交于点M,若 , 求点P的坐标;
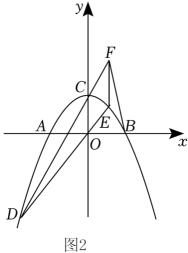
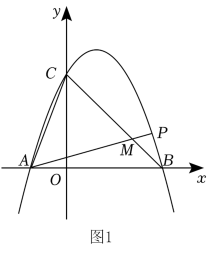 (2)、如图2,已知 , D为第三象限抛物线上一动点,直线交抛物线于另一点E,轴交直线于点F,连接 , 求出的最小值及此时点D的坐标.
(2)、如图2,已知 , D为第三象限抛物线上一动点,直线交抛物线于另一点E,轴交直线于点F,连接 , 求出的最小值及此时点D的坐标.