江苏省宿迁市沭阳县2022-2023学年七年级下学期期中数学试题

试卷更新日期：2023-06-08 类型：期中考试

进入出卷网下载

一、单选题

1. 将如图所示的图案通过平移后，可以得到的图案是（）

A、 B、 C、 D、

查看试题解析
2. 已知一个三角形的两边长分别为1，4，则第三边长可以是（）

A、2 B、3 C、4 D、5

查看试题解析
3. 下列运算正确的是（）

A、 ${(a^{4})}^{3} = a^{7}$ B、 $a^{3} \cdot a^{2} = a^{6}$ C、 ${(a - 3)}^{2} = a^{2} - 9$ D、 $12 a^{2} \div 3 a = 4 a$

查看试题解析
4. 如图，点E在 $B C$ 的延长线上，下列条件中能判断 $A B ∥ C D$ （）

A、 $∠ 3 = ∠ 4$ B、 $∠ D = ∠ D C E$ C、 $∠ D + ∠ B C D = 180 °$ D、 $∠ 1 = ∠ 2$

查看试题解析
5. 墨迹覆盖了等式“ $a^{3} ？ a^{3} = 2 a^{3} (a \neq 0)$ ”中的运算符号，则覆盖的是（）

A、+ B、 $-$ C、× D、÷

查看试题解析
6. 如图，四边形 $A B C D$ 中， $∠ A = 140 °$ ， $∠ B = 60 °$ ， $∠ A D C$ 、 $∠ B C D$ 的平分线相交于点E，则 $∠ C E D =$ （）

A、 $70 °$ B、 $100 °$ C、 $120 °$ D、 $90 °$

查看试题解析
7. 计算 $(a - b) (a + b) (a^{2} + b^{2}) (a^{4} + b^{4})$ 的结果是（）

A、 $a^{8} - b^{8}$ B、 $a^{8} - 2 a^{4} b^{4} + b^{8}$ C、 $a^{8} + 2 a^{4} b^{4} + b^{8}$ D、 $a^{8} + b^{8}$

查看试题解析
8. $△ A B C$ 中， $∠ A = m °$ ， $∠ A B C$ 和 $∠ A C D$ 的平分线交于点 $A_{1}$ ，得 $∠ A_{1}$ ； $∠ A_{1} B C$ 和 $∠ A_{1} C D$ 的平分线交于点 $A_{2}$ ，得 $∠ A_{2}$ ；…… $∠ A_{2022} B C$ 和 $∠ A_{2022} C D$ 的平分线交于点 $A_{2023}$ ，则 $∠ A_{2023}$ 的度数为（）

A、 $(\frac{m}{2^{2021}}) °$ B、 $(\frac{m}{2^{2022}}) °$ C、 $(\frac{m}{2^{2023}}) °$ D、 $(\frac{m}{2^{2024}}) °$

查看试题解析

二、填空题

9. 小时候我们用肥皂水吹泡泡，其泡沫的厚度约0.000326毫米，0.000326毫米用科学记数法表示正确的是毫米.

查看试题解析
10. $2 a b^{2} \cdot a^{2} b =$ ．

查看试题解析
11. 若式子 ${(x - 5)}^{0}$ 有意义，则实数x的取值范围是．

查看试题解析
12. 如果一个多边形的每一个外角都等于45°，那么这个多边形的边数是．

查看试题解析
13. 如图，在 $△ A B C$ 中，点E是 $A C$ 的中点，点F是 $B E$ 的中点，且 $S_{△ A B C} = 20 c m^{2}$ ，则阴影部分的面积为 $c m^{2}$ ．

查看试题解析
14. 我们约定 $a ※ b = 5^{a} \times 5^{b}$ ，如 $2 ※ 3 = 5^{2} \times 5^{3} = 5^{5}$ ．那么 $13 ※ 3 =$ ．

查看试题解析
15. 已知 $3^{m} \cdot 9^{n} = \frac{1}{27}$ ，则 $m + 2 n$ 的值= ．

查看试题解析
16. ${(- \frac{3}{2})}^{2023} \cdot {(\frac{2}{3})}^{2022} =$ ．

查看试题解析
17. 已知多项 $(x^{2} + x + 1)$ 式 $(x - 2 a)$ 与的乘积中不含 $x^{2}$ 项，则常数a的值是．

查看试题解析
18. 某兴趣小组利用几何图形画出螳螂的简笔画，如图，已知 $∠ B A C = 120 °$ ， $A B ∥ D E$ ， $∠ D = 80 °$ ，则 $∠ A C D =$ °．

查看试题解析

三、解答题

19. 计算

(1)、 ${(- 1)}^{2023} + {(3 - π)}^{0} - 3^{- 2}$

(2)、 $a^{2} \cdot a^{4} + a^{8} \div a^{2} - {(- 2 a^{2})}^{3}$

查看试题解析
20. 把下列各式因式分解

(1)、 $x^{2} - 16$

(2)、 $2 {(a - b)}^{2} - 2 (a - b)$

查看试题解析
21. 先化简，再求值： ${(a - 2 b)}^{2} + (3 a - 2 b) (a + 2 b)$ ，其中 $a = \frac{1}{2}$ ， $b = 4$ ．

查看试题解析
22. 如图， $∠ A B E$ 是四边形 $A B C D$ 的一个外角，且 $∠ A B E = ∠ D$ ．那么 $∠ A$ 与 $∠ C$ 互补吗？为什么？

查看试题解析
23. 如图，在每个小正方形的边长均为1的方格纸中， $△ A B C$ 的顶点都在方格纸的格点上．

(1)、 $△ A B C$ 的面积为；

(2)、将 $△ A B C$ 平移后得到 $△ A^{'} B^{'} C^{'}$ ，图中标出了点 $B$ 的对应点 $B^{'}$ ，请补全 $△ A^{'} B^{'} C^{'}$ ；

(3)、连接 $A A^{'} 、 B B^{'}$ ，则这两条线段之间的关系是；

(4)、点 $P$ 为格点，且 $S_{△ P B C} = S_{△ A B C}$ （点 $P$ 与点 $A$ 不重合），满足这样条件的 $P$ 点有个．

查看试题解析
24. 如图， $A F$ 分别与 $B D$ 、 $C E$ 相交于点 $G$ 、点 $H$ ， $∠ 1 + ∠ 2 = 180 °$ ， $∠ C = ∠ D$ ，则 $A C$ 与 $D F$ 平行吗？请说明理由．

查看试题解析
25. 若 $a^{m} = a^{n}$ （ $a > 0$ 且 $a \neq 1$ ， m、n是正整数），则 $m = n$ ．利用上面结论解决下面的问题：

(1)、如果 $2^{x + 1} \cdot 2^{x} = 2^{5}$ ，求x的值；

(2)、如果 $2^{x + 1} + 2^{x} = 24$ ，求x的值．

查看试题解析
26. 阅读下面的材料：若 $m^{2} - 2 m n + 2 n^{2} - 8 n + 16 = 0$ ，求m，n的值．
解： $∵$ $m^{2} - 2 m n + 2 n^{2} - 8 n + 16 = 0$ ．

$∴$ $m^{2} - 2 m n + n^{2} + n^{2} - 8 n + 16 = 0$

$∴$ $(m^{2} - 2 m n + n^{2}) + (n^{2} - 8 n + 16) = 0$

$∴$ ${(m - n)}^{2} + {(n - 4)}^{2} = 0$ ．

$∴$ ${(m - n)}^{2} = 0$ ， ${(n - 4)}^{2} = 0$ ．

$∴$ $n = 4$ ， $m = 4$ ．

根据你的观察，探究下列问题：

(1)、若 $a^{2} - 6 a + 9 + b^{2} = 0$ ，则 $a =$ ， $b =$ ；

(2)、已知 $x^{2} - 2 x y + 2 y^{2} - 4 y + 4 = 0$ ，求 $x^{y}$ 的值；

(3)、已知 $△ A B C$ 的三边长a，b，c都是正整数，且满足 $a^{2} + b^{2} - 2 a - 6 b + 10 = 0$ ，求 $△ A B C$ 的周长．

查看试题解析
27. 我们已经知道，通过计算几何图形的面积可以表示一些代数恒等式．例如图1可以得到 ${(a + b)}^{2} = a^{2} + 2 a b + b^{2}$ ，基于此，请解答下列问题：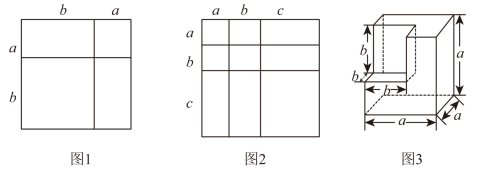

(1)、根据图2，写出一个代数恒等式：；

(2)、若 $a + b + c = 10$ ， $a b + a c + b c = 25$ ．则 $a^{2} + b^{2} + c^{2} =$ ；

(3)、在棱长为a的正方体上割去一个棱长为 $b (b < a)$ 的小正方体（如图3），通过用不同的方法计算图中余下几何体的体积，完成填空： $a^{3} - b^{3} = (a - b) (____________)$ ．

(4)、利用（3）得到的恒等式分解因式： $27 x^{3} - y^{3}$ ．

查看试题解析
28. 我们将内角互为对顶角的两个三角形称为“对顶三角形”．例如，在图1中， $△ A O B$ 的内角 $∠ A O B$ 与 $△ C O D$ 的内角 $∠ C O D$ 互为对顶角，则 $△ A O B$ 与 $△ C O D$ 为对顶三角形，根据三角形内角和定理知“对顶三角形”有如下性质： $∠ A + ∠ B = ∠ C + ∠ D$ ．

(1)、【性质理解】
如图2，在“对顶三角形” $△ A O B$ 与 $△ C O D$ 中， $∠ E A O = ∠ C$ ， $∠ D = 2 ∠ B$ ， $∠ D = 40 °$ ，则∠EAB=°；

(2)、【性质应用】
如图3， $∠ B A D$ 和 $∠ B C D$ 的平分线交于点E，则 $∠ E$ 与 $∠ D$ 、 $∠ B$ 之间存在何种数量关系．请说明理由；

(3)、【拓展提高】
如图4， $B E$ 、 $C D$ 是 $△ A B C$ 的角平分线，且 $∠ B D C$ 和 $∠ B E C$ 的平分线 $D P$ 和 $E P$ 相交于点P，设 $∠ A = α$ ，直接写出 $∠ P$ 的度数（用含 $α$ 的式子表示 $∠ P$ ）﹒

查看试题解析