河南省洛阳市伊川县2022-2023学年七年级下学期期中数学试题
试卷更新日期:2023-06-08 类型:期中考试
一、单选题
-
1. 方程3x=2x+7的解是( )A、x=4 B、x=﹣4 C、x=7 D、x=﹣72. 二元一次方程 ( )
A、有且只有一解 B、有无数解 C、无解 D、有且只有两解3. 解方程时,去分母正确的是( )A、 B、 C、 D、4. 2021年5月,由中国航天科技集团研制的天问一号探测器的着陆巡视器成功着陆于火星乌托邦平原南部预选着陆区,中国航天器首次奔赴火星,就“毫发未损”地顺利出现在遇远的红色星球上,完成了人类航天史上的一次壮举.火星与地球的最近距离约为5500万千米,该数据用科学记数法可表示为( )千米A、5.5×108 B、5.5×107 C、0.55×109 D、0.55×1085. 如图,AM∥BN , ∠ACB=90°,∠MAC=35°,则∠CBN的度数是( )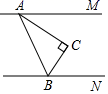 A、35° B、45° C、55° D、65°6. 已知线段 ,在直线AB上作线段BC , 使得 .若D是线段AC的中点,则线段AD的长为( )A、1 B、3 C、1或3 D、2或37. 如图是由4个相同的小正方体构成的一个组合体,该组合体的三视图中完全相同的是( )
A、35° B、45° C、55° D、65°6. 已知线段 ,在直线AB上作线段BC , 使得 .若D是线段AC的中点,则线段AD的长为( )A、1 B、3 C、1或3 D、2或37. 如图是由4个相同的小正方体构成的一个组合体,该组合体的三视图中完全相同的是( ) A、主视图和左视图 B、主视图和俯视图 C、左视图和俯视图 D、三个视图均相同8. 已知x,y的方程组与有相同的解,则a和b的值为( )A、 B、 C、 D、9. 下列用数轴表示不等式组 的解集正确的是( )A、
A、主视图和左视图 B、主视图和俯视图 C、左视图和俯视图 D、三个视图均相同8. 已知x,y的方程组与有相同的解,则a和b的值为( )A、 B、 C、 D、9. 下列用数轴表示不等式组 的解集正确的是( )A、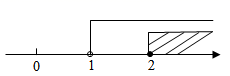 B、
B、 C、
C、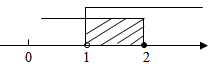 D、
D、 10. 洛书被世界公认为组合数字的鼻祖,它是中华民族对人类伟大贡献之一,它是在一个正方形方格中,每个小方格内均有不同的数,任意一横行,一纵列及对角线的几个数之和都相等.如图是一个洛书,上面只有部分数字可见,则对应的数是( )
10. 洛书被世界公认为组合数字的鼻祖,它是中华民族对人类伟大贡献之一,它是在一个正方形方格中,每个小方格内均有不同的数,任意一横行,一纵列及对角线的几个数之和都相等.如图是一个洛书,上面只有部分数字可见,则对应的数是( ) A、1 B、4 C、6 D、8
A、1 B、4 C、6 D、8二、填空题
-
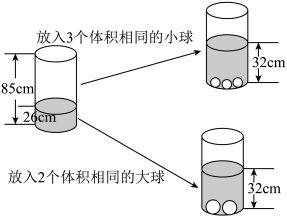
11. 单项式的系数是 , 次数是.12. 已知 , 则代数式的值是 .13. 不等式组的所有整数解的和为.14. 根据下图中给出的信息,如果放入大、小球共10个,水面上升到 , 那么应放入个大球.
 15. 为了求的值,可令 , 则 , 因此, , 所以即 , 依照以上推理计算:的值是 .
15. 为了求的值,可令 , 则 , 因此, , 所以即 , 依照以上推理计算:的值是 .三、解答题
-
16.(1)、解方程:;(2)、计算:17. 先化简,再求值: , 其中 , .18. 解方程组19. 解不等式组 , 并求其负整数的解.20. 《九章算术》是我国古代乃至东方的第一部自成体系的数学专著,它系统地总结了战国、秦、汉时期的数学成就,标志着以筹算为基础的中国古代数学体系的正式形成.《九章算术》全书收集了246个数学问题并提出其解法,其中的许多数学问题是世界上记载最早的.《九章算术》卷第七“盈不足”有如下记载.原文:今有共买琎① , 人出半,盈四;人出少半,不足三.问人数、琎价各几何?注释:①琎(jīn):像玉的石头.译文:今有人合伙买琎石,每人出钱,会多4钱;每人出钱,又差3钱.问人数、琎价各是多少?21. 水是万物生命之源,但随着人口急剧增长,水资源透支令人担忧,节约用水迫在眉睫,某城市为了避免居民用水浪费现象,制定了居民每月每户用水标准为 ,收费为正常标准,如果超标用水,超过部分加价收费,下表是小明家2014年两个月的收费表:
时间 项目
用水量/
费用/元
11月
15
35
12月
18
44
请问该城市居民标准内用水及超标用水的价格是如何制定的?