广西壮族自治区贵港市港南区2022-2023学年八年级下学期期中数学试题
试卷更新日期:2023-06-08 类型:期中考试
一、单选题
-
1. 下列几组数中,能构成直角三角形三边长的是( )A、1,2,3 B、2,3,4 C、3,4,5 D、4,5,62. 在下列图形中,既是轴对称图形,又是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 3. 若直角三角形的斜边长为12,则斜边上的中线长为( )A、6 B、8 C、10 D、124. 到三角形三条边的距离都相等的点是( )A、两条中线的交点 B、两条高的交点 C、两条角平线的交点 D、两条边的垂直平分线的交点5. 已知矩形的两条对角线、相交于点O,则下列结论不一定正确的是( )A、 B、 C、 D、6. 下列图形中,具有稳定性的是( )A、直角三角形 B、长方形 C、五边形 D、正六边形7. 在中, , , , 则的面积是( )A、 B、 C、 D、8. 如图,两个较大正方形的面积分别为 576、625,则字母 A所代表的正方形的边长为( )
3. 若直角三角形的斜边长为12,则斜边上的中线长为( )A、6 B、8 C、10 D、124. 到三角形三条边的距离都相等的点是( )A、两条中线的交点 B、两条高的交点 C、两条角平线的交点 D、两条边的垂直平分线的交点5. 已知矩形的两条对角线、相交于点O,则下列结论不一定正确的是( )A、 B、 C、 D、6. 下列图形中,具有稳定性的是( )A、直角三角形 B、长方形 C、五边形 D、正六边形7. 在中, , , , 则的面积是( )A、 B、 C、 D、8. 如图,两个较大正方形的面积分别为 576、625,则字母 A所代表的正方形的边长为( ) A、1 B、49 C、16 D、79. 将一副直角三角板如图放置,使含角的三角板的短直角边和含角的三角板的一条直角边重合,则的度数为( )度.
A、1 B、49 C、16 D、79. 将一副直角三角板如图放置,使含角的三角板的短直角边和含角的三角板的一条直角边重合,则的度数为( )度.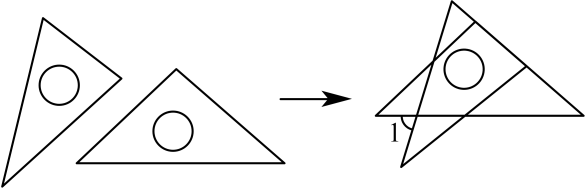 A、60 B、75 C、45 D、3010. 如图,为测量池塘两端的距离,可先在平地上取一个点 , 从点不经过池塘可以直接到达点和 , 连接 , , 分别取、的中点 , , 连接后,量出的长为12米,那么就可以算出 , 的距离是( )
A、60 B、75 C、45 D、3010. 如图,为测量池塘两端的距离,可先在平地上取一个点 , 从点不经过池塘可以直接到达点和 , 连接 , , 分别取、的中点 , , 连接后,量出的长为12米,那么就可以算出 , 的距离是( )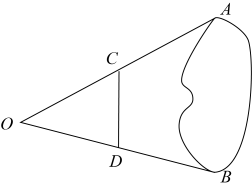 A、36米 B、24米 C、12米 D、6米11. 如图,在中, , , 于点 , , 若 , 分别为 , 的中点,则的长为( )
A、36米 B、24米 C、12米 D、6米11. 如图,在中, , , 于点 , , 若 , 分别为 , 的中点,则的长为( )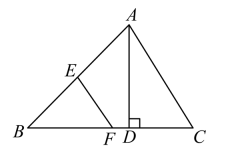 A、 B、 C、 D、12. 如图,菱形的对角线相交于点O,点E在上,连接 , 点F为的中点,连接 , 若 , , , 则线段的长为( )
A、 B、 C、 D、12. 如图,菱形的对角线相交于点O,点E在上,连接 , 点F为的中点,连接 , 若 , , , 则线段的长为( )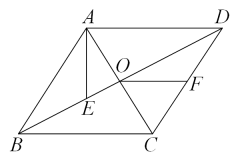 A、5 B、 C、 D、6
A、5 B、 C、 D、6二、填空题
-
13. 若一个多边形经过一个顶点的对角线将该多边形分成8个三角形,则该多边形为边形.14. 在△ABC中,AB=AC=5,BC=6,则△ABC的面积是 .15. 如图,在四边形中, , 若沿图中虚线剪去 , 则 .
 16. 如图,某研究性学习小组为测量学校A与河对岸水上乐园B之间的距离,在学校附近选一点C,利用测量仪器测得∠A=60°,∠C=90°,AC=1km.据此,可求得学校与水上乐园之间的距离AB等于 km.
16. 如图,某研究性学习小组为测量学校A与河对岸水上乐园B之间的距离,在学校附近选一点C,利用测量仪器测得∠A=60°,∠C=90°,AC=1km.据此,可求得学校与水上乐园之间的距离AB等于 km.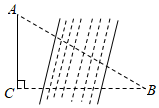 17. 如图,点O为直线上一点,过点O作射线 , 使 , 将一块透明的三角尺直角顶点放在点O处,并绕点O旋转一周,在旋转过程中,当直线恰好平分锐角时, .
17. 如图,点O为直线上一点,过点O作射线 , 使 , 将一块透明的三角尺直角顶点放在点O处,并绕点O旋转一周,在旋转过程中,当直线恰好平分锐角时, . 18. 《九章算术》中的“折竹抵地”问题:今有竹高一丈,末折抵地,去根六尺.问折高者几何?意思是:一根竹子,原高一丈(一丈=10尺),一阵风将竹子折断,其竹梢恰好抵地,抵地处离竹子底部6尺远,问折断处离地面的高度是多少?设折断处离地面的高度为x尺,则可列方程为 .
18. 《九章算术》中的“折竹抵地”问题:今有竹高一丈,末折抵地,去根六尺.问折高者几何?意思是:一根竹子,原高一丈(一丈=10尺),一阵风将竹子折断,其竹梢恰好抵地,抵地处离竹子底部6尺远,问折断处离地面的高度是多少?设折断处离地面的高度为x尺,则可列方程为 .三、解答题
-
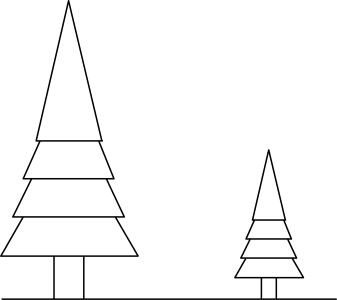
19. 一个n边形的每个外角都相等,如果它的内角与相邻外角的度数之比为 , 求n的值.20. 有两棵树,一棵高6米,另一棵高3米,两树相距4米,一只小鸟从一棵树的树梢飞到另一棵树的树梢,至少飞了多少米?
 21. 如图,在四边形中, , , , , 求:
21. 如图,在四边形中, , , , , 求: (1)、的长;(2)、四边形的面积.22. 如图,已知平行四边形 , 是的角平分线,交于点E
(1)、的长;(2)、四边形的面积.22. 如图,已知平行四边形 , 是的角平分线,交于点E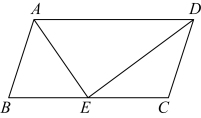 (1)、求证:;(2)、若点E是的中点, , 求的度数23. 如图,矩形的对角线交于点F,延长到点C,使 , 延长到点D,使 , 连接
(1)、求证:;(2)、若点E是的中点, , 求的度数23. 如图,矩形的对角线交于点F,延长到点C,使 , 延长到点D,使 , 连接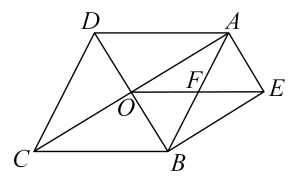 (1)、求证:四边形是菱形;(2)、若 , 求菱形的面积.24. 如图 , 是小朋友荡秋千的侧面示意图,静止时秋千位于铅垂线上,转轴到地面的距离乐乐在荡秋千过程中,当秋千摆动到最高点时,过点作于 , 点到地面的距离 , 当他从处摆动到处时, , 若 , 作 , 垂足为F.求到的距离 .
(1)、求证:四边形是菱形;(2)、若 , 求菱形的面积.24. 如图 , 是小朋友荡秋千的侧面示意图,静止时秋千位于铅垂线上,转轴到地面的距离乐乐在荡秋千过程中,当秋千摆动到最高点时,过点作于 , 点到地面的距离 , 当他从处摆动到处时, , 若 , 作 , 垂足为F.求到的距离 .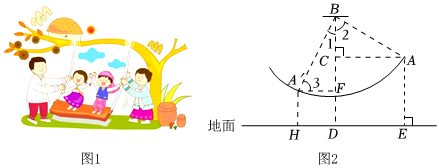
四、填空题
-
25. 探究归纳题:
 (1)、试验分析:
(1)、试验分析:如图1,经过A点可以作条对角线;同样,经过B点可以作条;经过C点可以作条;经过D点可以作条对角线.
通过以上分析和总结,图1共有条对角线.
(2)、拓展延伸:运用(1)的分析方法,可得:
图2共有条对角线;
图3共有条对角线;
(3)、探索归纳:对于n边形(n>3),共有条对角线.(用含n的式子表示)
(4)、特例验证:十边形有条对角线.
五、解答题
-
26. 如图,已知长方形ABCD的长AB=a米,宽BC=b米,a,b满足 , 一动点P从A出发以每秒1米的速度沿着运动,另一动点Q从B出发以每秒2米的速度沿运动,P,Q同时出发,运动时间为t.
 (1)、a= , b= ;(2)、当t=4.5时,求△APQ的面积;(3)、当P,Q都在DC上,且PQ距离为1时,求t的值.
(1)、a= , b= ;(2)、当t=4.5时,求△APQ的面积;(3)、当P,Q都在DC上,且PQ距离为1时,求t的值.
-