广西壮族自治区防城港市防城区2022-2023学年七年级下学期期中数学试题
试卷更新日期:2023-06-08 类型:期中考试
一、单选题
-
1. 9的算术平方根是( )A、3 B、 C、81 D、2. 在 , , 0,中,有理数有( )个A、4 B、3 C、2 D、13. 下列四个图形中,不能通过基本图形平移得到的是( )A、
 B、
B、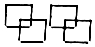 C、
C、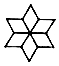 D、
D、 4. 在平面直角坐标系中,点 所在的象限是( )A、第一象限 B、第二象限 C、第三象限 D、第四象限5. 下列说法正确的是( )A、是的平方根 B、5是的算术平方根 C、的平方根是3 D、8的立方根是6. 有一个数值转换器,原理如图所示,当输入r为27时,输出y的值是( )
4. 在平面直角坐标系中,点 所在的象限是( )A、第一象限 B、第二象限 C、第三象限 D、第四象限5. 下列说法正确的是( )A、是的平方根 B、5是的算术平方根 C、的平方根是3 D、8的立方根是6. 有一个数值转换器,原理如图所示,当输入r为27时,输出y的值是( ) A、3 B、 C、 D、7. 如图,在数轴上表示的点可能是( )
A、3 B、 C、 D、7. 如图,在数轴上表示的点可能是( )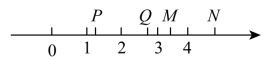 A、点P B、点Q C、点M D、点N8. 如图所示,点E在AC的延长线上,下列条件中能判断AB∥CD的是( )
A、点P B、点Q C、点M D、点N8. 如图所示,点E在AC的延长线上,下列条件中能判断AB∥CD的是( )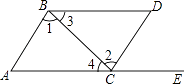 A、∠3=∠4 B、∠1=∠2 C、∠D=∠DCE D、∠D+∠ACD=180°9. 已知线段CD是由线段AB平移得到的,点A(–1,4)的对应点为C(4,7),则点B(–4,–1)的对应点D的坐标为( )A、(1,2) B、(2,9) C、(5,3) D、(–9,–4)10. 如图, , , 平分 , 则为( )
A、∠3=∠4 B、∠1=∠2 C、∠D=∠DCE D、∠D+∠ACD=180°9. 已知线段CD是由线段AB平移得到的,点A(–1,4)的对应点为C(4,7),则点B(–4,–1)的对应点D的坐标为( )A、(1,2) B、(2,9) C、(5,3) D、(–9,–4)10. 如图, , , 平分 , 则为( ) A、 B、 C、 D、11. 满足的整数x有( )A、4个 B、5个 C、6个 D、7个12. 如图,在中, , , 面积是10;的垂直平分线分别交 , 边于E、D两点,若点F为边的中点,点P为线段上一动点,则周长的最小值为( )
A、 B、 C、 D、11. 满足的整数x有( )A、4个 B、5个 C、6个 D、7个12. 如图,在中, , , 面积是10;的垂直平分线分别交 , 边于E、D两点,若点F为边的中点,点P为线段上一动点,则周长的最小值为( ) A、7 B、9 C、10 D、14
A、7 B、9 C、10 D、14二、填空题
-
13. 如果电影票用表示2排6座,那么7排5座可表示为 .14. 比较大小: .(填“<”或“>”)15. 若点M(a+2,a-3)在x轴上,则点M的坐标为 .16. 一个正数a的两个平方根是 和 ,则 的立方根为 .17. 实数a,b在数轴上的位置如图所示,则 .
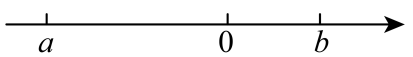 18. 一块直角三角板按图所示方式放置在一张矩形纸条上.若 , 则的度数为 .
18. 一块直角三角板按图所示方式放置在一张矩形纸条上.若 , 则的度数为 .
三、解答题
-
19. 计算:20. 已知与互为相反数.求的平方根.21. 完成下面的证明:
已知:如图,∠1=30°,∠B=60°,AB⊥AC.求证:AD∥BC.

证明:∵AB⊥AC(已知)
∴∠ ▲ =90°( )
∵∠1=30°,∠B=60°(已知)
∴∠1+∠BAC+∠B= ▲ ( )
即∠ ▲ +∠B=180°
∴AD∥BC( )
22. 如图,在平面直角坐标系中,已知点A(0,-2),B(3,-1),将线段AB先向左平移2个单位长度,再向上平移3个单位长度得到线段A1B1 .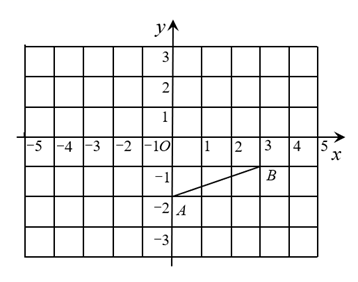 (1)、请直接写出A,B两点的对应点A1 , B1的坐标;(2)、在平面直角坐标系中画出线段A1B1;(3)、连接OA1 , OB1 , 求三角形A1OB1的面积.23. 如图,直线相交于点O.
(1)、请直接写出A,B两点的对应点A1 , B1的坐标;(2)、在平面直角坐标系中画出线段A1B1;(3)、连接OA1 , OB1 , 求三角形A1OB1的面积.23. 如图,直线相交于点O.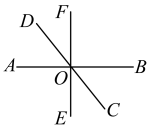 (1)、写出图中的邻补角是 , 的对顶角是;(2)、若 , 求和的度数.24. 如图,在四边形中, , .
(1)、写出图中的邻补角是 , 的对顶角是;(2)、若 , 求和的度数.24. 如图,在四边形中, , .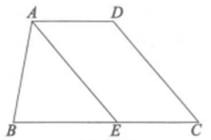 (1)、求的度数;(2)、平分交于点 , .求证:.
(1)、求的度数;(2)、平分交于点 , .求证:.
