广西壮族自治区防城港市防城区2022-2023学年八年级下学期期中数学试题
试卷更新日期:2023-06-08 类型:期中考试
一、单选题
-
1. 使 有意义的x的取值范围是( )
A、x≤3 B、x<3 C、x≥3 D、x>32. 若最简二次根式与是同类二次根式,则m=( )A、2021 B、2023 C、2 D、13. 下列运算错误的是( )A、 B、 C、 D、4. 以下列各组数据为边长作三角形,其中不能组成直角三角形的是( )A、4,6,8 B、5,12,13 C、6,8,10 D、7,24,255. 在中,点D,E分别是 , 上的点,且 , 点F是延长线上一点,连接 . 添加下列条件后,不能判断四边形是平行四边形的是( ) A、 B、 C、 D、6. 下列命题的逆命题是假命题的是( )A、在同一个三角形中,等边对等角 B、两直线平行,同位角相等 C、两直线平行,内错角相等 D、对顶角相等7. 如图,这是一株美丽的勾股树,所有的四边形都是正方形,所有的三角形都是直角三角形,若正方形A、B、C、D的边长是3、5、2、3,则最大正方形的面积是( )
A、 B、 C、 D、6. 下列命题的逆命题是假命题的是( )A、在同一个三角形中,等边对等角 B、两直线平行,同位角相等 C、两直线平行,内错角相等 D、对顶角相等7. 如图,这是一株美丽的勾股树,所有的四边形都是正方形,所有的三角形都是直角三角形,若正方形A、B、C、D的边长是3、5、2、3,则最大正方形的面积是( )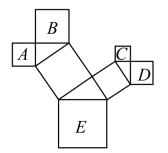 A、13 B、47 C、 D、8. 已知四边形是平行四边形,对角线、交于点O,E是的中点,以下说法错误的是( )
A、13 B、47 C、 D、8. 已知四边形是平行四边形,对角线、交于点O,E是的中点,以下说法错误的是( )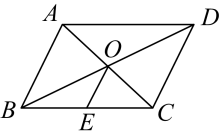 A、 B、 C、 D、9. 如图,在矩形ABCD中,对角线AC、BD相交于点O,交BD于点E, , 则的度数为( )
A、 B、 C、 D、9. 如图,在矩形ABCD中,对角线AC、BD相交于点O,交BD于点E, , 则的度数为( ) A、40° B、35° C、30° D、25°10. 若 是整数,则正整数n的最小值是( )A、4 B、5 C、6 D、711. 如图,一圆柱高 , 底面周长是 , 为的中点,一只蚂蚁从点沿圆柱外壁爬到点处吃食,要爬行的最短路程是( )
A、40° B、35° C、30° D、25°10. 若 是整数,则正整数n的最小值是( )A、4 B、5 C、6 D、711. 如图,一圆柱高 , 底面周长是 , 为的中点,一只蚂蚁从点沿圆柱外壁爬到点处吃食,要爬行的最短路程是( )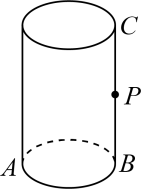 A、 B、 C、 D、12. 如图是一个按某种规律排列的数阵,根据数阵排列的规律,第2023行从左向右数第2022个数是( )
A、 B、 C、 D、12. 如图是一个按某种规律排列的数阵,根据数阵排列的规律,第2023行从左向右数第2022个数是( ) A、 B、 C、 D、2022
A、 B、 C、 D、2022二、填空题
-
13. 比较大小: .14. 已知平行四边形ABCD中,∠A+∠C=110°,则∠B的度数为 .15. 如图,Rt△ABC中,∠ACB=90°,AB=6,D是AB的中点,则CD= .
 16. 在平面直角坐标系中,点(3,﹣2)到原点的距离是 .17. 实数a、b在数轴上的位置如下图所示,则化简结果为 .
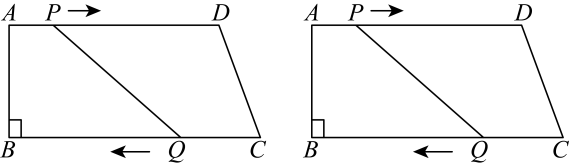
16. 在平面直角坐标系中,点(3,﹣2)到原点的距离是 .17. 实数a、b在数轴上的位置如下图所示,则化简结果为 .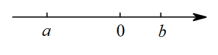 18. 如图,在中, , P为边上一动点,于点E,于F,则的最小值为 .
18. 如图,在中, , P为边上一动点,于点E,于F,则的最小值为 .
三、解答题
-
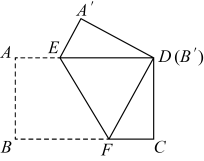
19. 计算:(1)、(2)、20. 计算:21. 如图,点B,E,C,F在一条直线上,AB=DE, , BE=CF.
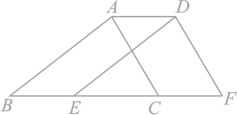 (1)、求证:△ABC≌△DEF;(2)、连接AD,求证:四边形ACFD是平行四边形.22. 如图,在四边形中, , , . 求四边形的面积.
(1)、求证:△ABC≌△DEF;(2)、连接AD,求证:四边形ACFD是平行四边形.22. 如图,在四边形中, , , . 求四边形的面积. 23. 如图,已知的对角线 , 交于点O,过点O且与 , 分别相交于点E、F.
23. 如图,已知的对角线 , 交于点O,过点O且与 , 分别相交于点E、F. (1)、求证:;(2)、若 , , , 求的长.24. 如图,是矩形边上的两点, .
(1)、求证:;(2)、若 , , , 求的长.24. 如图,是矩形边上的两点, .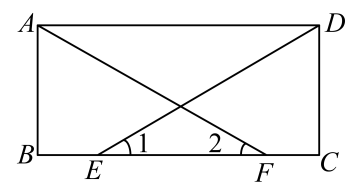 (1)、求证:;(2)、若求矩形的面积(结果保留根号).
(1)、求证:;(2)、若求矩形的面积(结果保留根号).