广西南宁市部分地区2022-2023学年八年级下学期期中数学试题
试卷更新日期:2023-06-08 类型:期中考试
一、单选题
-
1. 下列各式一定是二次根式的是( )A、1 B、 C、 D、2. 太阳的半径约为369000千米,用科学记数法表示为( )A、 B、 C、 D、3. 下列各组数中,能构成直角三角形的是( )A、1、2、3 B、3、4、5 C、7、8、9 D、5、10、204. 下列各式中能与合并的二次根式是( )A、 B、 C、2 D、5. 下列计算正确的是( )A、 B、 C、 =1 D、 =26. 如图,要使▱成为矩形,需要添加的条件是( )
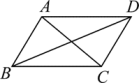 A、 B、 C、 D、7. 实数在数轴上的位置如图所示,则化简后为( )
A、 B、 C、 D、7. 实数在数轴上的位置如图所示,则化简后为( ) A、2 B、 C、 D、无法确定8. 如图所示的“赵爽弦图”是由四个全等的直角三角形和一个小正方形拼成的一个大正方形,设直角三角形较长直角边长为a , 较短直角边长为b.若 ,大正方形的面积为25,则小正方形的边长为( )
A、2 B、 C、 D、无法确定8. 如图所示的“赵爽弦图”是由四个全等的直角三角形和一个小正方形拼成的一个大正方形,设直角三角形较长直角边长为a , 较短直角边长为b.若 ,大正方形的面积为25,则小正方形的边长为( )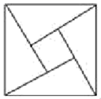 A、9 B、6 C、4 D、39. 如图,的顶点A的坐为 , 若边的长为4,则顶点D的坐标是( )
A、9 B、6 C、4 D、39. 如图,的顶点A的坐为 , 若边的长为4,则顶点D的坐标是( ) A、 B、 C、 D、10. 如图,菱形的对角线、相交于点 , 为的中点,若菱形的周长为 , 则OE的长为( )
A、 B、 C、 D、10. 如图,菱形的对角线、相交于点 , 为的中点,若菱形的周长为 , 则OE的长为( ) A、2 B、1 C、4 D、311. 我国明代有一位杰出的数学家提出一道“荡秋千”的数学问题:“平地秋千未起,踏板一尺离地,送行二步与人齐,五尺人高曾记;仕女佳人争蹴,终朝笑语欢嬉,良工高士素好奇,算出索长有几?”其意思为:如图所示,当秋千静止在地面上时,秋千的踏板离地的距离为一尺(尺),将秋千的踏板往前推两步(每一步合五尺,即尺),秋千的踏板与人一样高,这个人的身高为五尺(尺),求这个秋千的绳索有多长?( )
A、2 B、1 C、4 D、311. 我国明代有一位杰出的数学家提出一道“荡秋千”的数学问题:“平地秋千未起,踏板一尺离地,送行二步与人齐,五尺人高曾记;仕女佳人争蹴,终朝笑语欢嬉,良工高士素好奇,算出索长有几?”其意思为:如图所示,当秋千静止在地面上时,秋千的踏板离地的距离为一尺(尺),将秋千的踏板往前推两步(每一步合五尺,即尺),秋千的踏板与人一样高,这个人的身高为五尺(尺),求这个秋千的绳索有多长?( ) A、12尺 B、尺 C、尺 D、尺12. 如图,正方形的边长为 , 点在上,且 , 是上的一动点,则的最小值是( )
A、12尺 B、尺 C、尺 D、尺12. 如图,正方形的边长为 , 点在上,且 , 是上的一动点,则的最小值是( )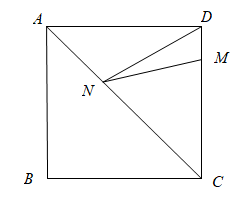 A、20 B、25 C、30 D、35
A、20 B、25 C、30 D、35二、填空题
-
13. 若式子在实数范围内有意义,则的取值范围 .14. 计算 的结果是.15. 如图,在▱中,若 , 则度.
 16. 如图,一棵垂直于地面的大树在离地面3米处折断,树的顶端落在离树干底部4米处,那么这棵树折断之前的高度是米.
16. 如图,一棵垂直于地面的大树在离地面3米处折断,树的顶端落在离树干底部4米处,那么这棵树折断之前的高度是米. 17. 如图,将矩形ABCD沿EF折叠,使顶点C恰好落在AB边的中点C′上.若AB=6,BC=9,则BF的长为
17. 如图,将矩形ABCD沿EF折叠,使顶点C恰好落在AB边的中点C′上.若AB=6,BC=9,则BF的长为 18. 如图,等腰直角三角形的两直角边分别为 , 以斜边为边作第二个等腰直角三角形 , 再以斜边为边作第三个等腰直角三角形 , 如此进行下去……记等腰直角三角形的直角边长为 , 按上述方法所作的等腰直角三角形的直角边依次为 , 则 .
18. 如图,等腰直角三角形的两直角边分别为 , 以斜边为边作第二个等腰直角三角形 , 再以斜边为边作第三个等腰直角三角形 , 如此进行下去……记等腰直角三角形的直角边长为 , 按上述方法所作的等腰直角三角形的直角边依次为 , 则 .
三、解答题
-
19. 计算: .20. 先化简,再求值: .21. 如图,已知▱ , 延长到 , 使 , 连接 , , , 若 .
 (1)、求证:;(2)、求证:四边形是矩形.22. 如图,已知 .
(1)、求证:;(2)、求证:四边形是矩形.22. 如图,已知 .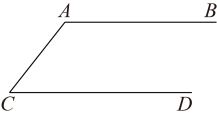 (1)、求作:的平分线 , 交于点E(要求:尺规作图,保留作图痕迹,不写作法);(2)、已知 , 求的度数.23. 如图,菱形花坛的边长为 , , 沿着菱形的对角线修建了两条小路和 .
(1)、求作:的平分线 , 交于点E(要求:尺规作图,保留作图痕迹,不写作法);(2)、已知 , 求的度数.23. 如图,菱形花坛的边长为 , , 沿着菱形的对角线修建了两条小路和 . (1)、求两条小路和的长.(结果保留根号)(2)、花坛的面积.(结果保留根号)24. 如图,永定路一侧有A、B两个送奶站,C为永定路上一供奶站,和为供奶路线,现已测得 , , , .
(1)、求两条小路和的长.(结果保留根号)(2)、花坛的面积.(结果保留根号)24. 如图,永定路一侧有A、B两个送奶站,C为永定路上一供奶站,和为供奶路线,现已测得 , , , . (1)、连接 , 求两个送奶站之间的距离.(2)、有一人从点C处出发,沿永定路路边向右行走,速度为 , 多长时间后这个人距B送奶站最近?25. 观察下列各式及其验算过程:
(1)、连接 , 求两个送奶站之间的距离.(2)、有一人从点C处出发,沿永定路路边向右行走,速度为 , 多长时间后这个人距B送奶站最近?25. 观察下列各式及其验算过程:=2 ,验证: = = =2 ;
=3 ,验证: = = =3
(1)、按照上述两个等式及其验证过程的基本思路,猜想 的变形结果并进行验证.(2)、针对上述各式反映的规律,写出用n(n为大于1的整数)表示的等式并给予验证.26. 如图,点D从点A出发沿方向以2cm/s的速度向点B匀速运动,同时点E从点B出发沿方向以1cm/s的速度向点C匀速运动,当其中一个点到达终点时,另一个点也随之停止运动,设点D、E运动的时间为t秒(0<t<20),过点D作于点F,连接 , . (1)、求证:四边形是平行四边形;(2)、四边形能成为菱形吗?如果能,求相应的t的值,如果不能,说明理由;(3)、当t为何值时? .
(1)、求证:四边形是平行四边形;(2)、四边形能成为菱形吗?如果能,求相应的t的值,如果不能,说明理由;(3)、当t为何值时? .