河南省安阳市汤阴县2022-2023学年八年级下学期期中数学试题
试卷更新日期:2023-06-08 类型:期中考试
一、单选题
-
1. 若式子在实数范围内有意义,则x的取值范围是( )A、 B、 C、 D、
-
2. 下列运算正确的是( )A、 B、 C、 D、
-
3. 在中,的对边分别是a,b,c,下列条件中,不能判定是直角三角形的是( )A、 B、 C、 , , D、
-
4. 如图,下面不能判断是平行四边形的是( )
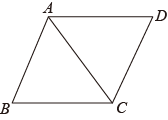 A、 , B、 , C、 , D、 ,
A、 , B、 , C、 , D、 , -
5. 下列命题,其中是真命题的为( )A、顺次连接任意四边形的各边中点得到的四边形一定是平行四边形 B、对角线互相垂直的四边形是菱形 C、对角线相等的四边形是矩形 D、一组邻边相等的平行四边形是正方形
-
6. 小明用四根长度相同的木条制作了能够活动的菱形学具,他先活动学具成为图1所示菱形,并测得∠B=60°,对角线AC=10cm,接着活动学具成为图2所示正方形,则图2中对角线AC的长为( )
 A、10cm B、20cm C、30cm D、cm
A、10cm B、20cm C、30cm D、cm -
7. 如图,在平行四边形 中, 、 是 上两点, ,连接 、 、 、 ,添加一个条件,使四边形 是矩形,这个条件是( )
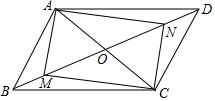 A、 B、 C、 D、
A、 B、 C、 D、 -
8. 一个正方形的面积是21,把此正方形的边长增加1,则新的正方形的边长范围是( )A、4与5之间 B、5与6之间 C、6与7之间 D、7与8之间
-
9. 用两块完全相同的直角三角形拼下列图形:①平行四边形;②矩形;③菱形;④正方形;⑤等腰三角形;⑥等边三角形,一定能拼成的图形是( )A、①④⑤ B、②⑤⑥ C、①②③ D、①②⑤
-
10. 如图,在菱形中, , , 点P是菱形内部一点,且满足 , 则的最小值是( )
 A、 B、 C、6 D、
A、 B、 C、6 D、
二、填空题
-
11. 如果最简二次根式与是同类二次根式,那么a的值是 .
-
12. 工人师傅常常通过测量平行四边形零件的对角线是否相等来检验零件是否为矩形,请问工人师傅此种检验方法依据的道理是.
-
13. 如图,在RtABC中,∠C=90°,AC=6,AB=10,点D、E、F是三边的中点,则DEF的周长是 .

-
14. 中国结,象征着中华民族的历史文化与精神.利用所学知识抽象出如图所示的菱形 , 测得 , , 直线交两对边于E、F,则的长为cm.

-
15. 如图,长方形ABCD的面积为20 , 对角线交于点O;以AB、AO为邻边作平行四边形 , 连接 , 交BD于;以AB、为邻边作平行四边形;…;依此类推,则平行四边形的面积为 .

三、解答题
-
16. 计算(1)、(2)、
-
17. 如图,在每个小正方形的边长为1的网格中,点A、B、C均在格点上.
 (1)、直接写出AC的长为 , △ABC的面积为;(2)、请在如图所示的网格中,用无刻度的直尺作出AC边上的高BD,并保留作图痕迹;(3)、求BD的长.
(1)、直接写出AC的长为 , △ABC的面积为;(2)、请在如图所示的网格中,用无刻度的直尺作出AC边上的高BD,并保留作图痕迹;(3)、求BD的长. -
18. 在学习了二次根式的性质后,小新同学用相关知识解决了下面这道题.
化简求值: , 其中
他的做法为:解:原式
当时,原式
小新同学的做法正确吗?若正确请说明理由,若不正确请把正确过程写出来.
-
19. 如图,在△ABC中,AB=AC,D为BC边的中点,过点作DE⊥AB,DF⊥AC,垂足分别为E,F.
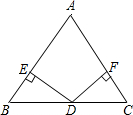 (1)、求证:△BED≌△CFD;(2)、当∠A=90°时,试判断四边形DFAE是什么特殊四边形?并说明理由.
(1)、求证:△BED≌△CFD;(2)、当∠A=90°时,试判断四边形DFAE是什么特殊四边形?并说明理由. -
20. 已知线段a,b,c,且线段a,b满足|a-|+(b-)2=0(1)、求a,b的值;(2)、若a,b,c是某直角三角形的三条边的长度,求c的值.
-
21. 如图,在四边形 中, , 的面积为 , , , .
 (1)、试判断 的形状;(2)、求四边形 的面积.
(1)、试判断 的形状;(2)、求四边形 的面积. -
22. 如图,平行四边形ABCD的对角线AC与BD相交于点O,点E为AO的中点,过点A作AF∥BD交BE的延长线于点F,连接DF.
 (1)、求证:四边形AODF是平行四边形;(2)、填空:
(1)、求证:四边形AODF是平行四边形;(2)、填空:①当△ACD满足条件时,四边形AODF是菱形.
②当△ACD满足条件时,四边形AODF是矩形.
-
23. 小新学习了特殊的四边形一平行四边形后,对特殊四边形的探究产生了兴趣,发现另外一类特殊四边形,如图1,我们把两条对角线互相垂直的四边形叫做垂美四边形.
 (1)、概念理解:在平行四边形、矩形、菱形、正方形中,一定是垂美四边形的是 .(2)、性质探究:通过探究,直接写出垂美四边形的面积S与两对角线 , 之间的数量关系: .(3)、问题解决:如图2,分别以的直角边和斜边为边向外作正方形和正方形 , 连接已知 , .
(1)、概念理解:在平行四边形、矩形、菱形、正方形中,一定是垂美四边形的是 .(2)、性质探究:通过探究,直接写出垂美四边形的面积S与两对角线 , 之间的数量关系: .(3)、问题解决:如图2,分别以的直角边和斜边为边向外作正方形和正方形 , 连接已知 , .①求证:四边形为垂美四边形;
②直接写出四边形的面积.
