2023年深圳市初中学业水平测试数学仿真模拟测试(5)
试卷更新日期:2023-06-06 类型:中考模拟
一、单选题(每题3分,共30分)
-
1. 若 , 则“□”内应填的实数是( )A、 B、2022 C、 D、2. 如图,将棱长为6的正方体截去一个棱长为3的正方体后,得到一个新的几何体,这个几何体的主视图是( )
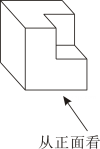 A、
A、 B、
B、 C、
C、 D、
D、 3. 某公司有10名员工,每人年收入数据如下表:
3. 某公司有10名员工,每人年收入数据如下表:年收入/万元
4
6
8
10
人数/人
3
4
2
1
则他们年收入数据的众数与中位数分别为( )
A、4,6 B、6,6 C、4,5 D、6,54. 2023年《政府工作报告》提出,“义务教育优质均衡发展”.根据预算报告,支持学前教育发展资金安排250亿元、增加20亿元,扩大普惠性教育资源供给.其中250亿元用科学记数法表示为( )A、元 B、元 C、元 D、元5. 下列运算正确的是( )A、 B、 C、 D、6. 将不等式组 的解集表示在数轴上,正确的是( )A、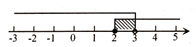 B、
B、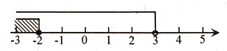 C、
C、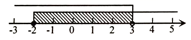 D、
D、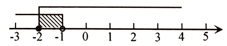 7. 一把直尺与含30°的直角三角板如图所示放置,∠1=40°,则∠2的度数是( )
7. 一把直尺与含30°的直角三角板如图所示放置,∠1=40°,则∠2的度数是( )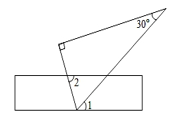 A、 B、 C、 D、8. 如图,在中,添加下列条件仍不能判定是菱形的是( )
A、 B、 C、 D、8. 如图,在中,添加下列条件仍不能判定是菱形的是( )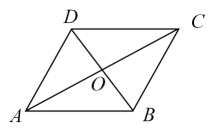 A、ACBD B、AB=BC C、AC=BD D、9. 如图,面积为64的正方形 ,分成4个全等的长方形和一个面积为4的小正方形,则小长方形的长和宽分别是( )
A、ACBD B、AB=BC C、AC=BD D、9. 如图,面积为64的正方形 ,分成4个全等的长方形和一个面积为4的小正方形,则小长方形的长和宽分别是( )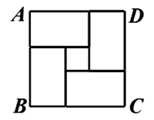 A、32,2 B、16,1 C、8,2 D、5,310. 如图,为的直径,与相切于点 , 交的延长线于点 , 且 . 若 , 则半径长为( )
A、32,2 B、16,1 C、8,2 D、5,310. 如图,为的直径,与相切于点 , 交的延长线于点 , 且 . 若 , 则半径长为( )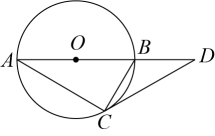 A、2 B、3 C、 D、
A、2 B、3 C、 D、二、填空题(每空3分,共15分)
-
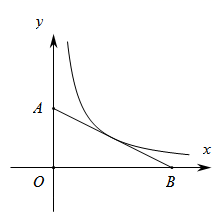
11. 分解因式: =.12. 在一个不透明的布袋中有白球和黑球共20个,这些球除颜色外都相同.小明将布袋中的球搅拌均匀,从中随机摸出一个球,记下它的颜色后再放回布袋中.不断重复这一过程,共摸了100次球,发现有40次摸到黑球,则布袋中黑球的个数可能为 .13. 等腰三角形三边长分别为 ,且 是关于 的一元二次方程 的两根,则n的值为14. 如图,已知直线y=mx+4分别与y轴,x轴交于A,B两点,且△ABO的面积为16,反比例函数的图象恰好经过AB的中点,则反比例函数的表达式为.
 15. 如图,在矩形ABCD中,E为BC边上一点, , 且 , , 则CE的长为 .
15. 如图,在矩形ABCD中,E为BC边上一点, , 且 , , 则CE的长为 .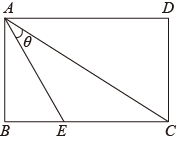
三、解答题(共7题,共55分)
-
16. 计算:(-1)2021 + ·cos30°-( )-117. 化简 ,并求值,其中 与 、 构成 的三边,且 为整数.18. 为了了解全校1800名学生对学校设置的体操、球类、跑步、踢毽子等课外体育活动项目的喜爱情况,在全校范围内随机抽取了若干名学生.对他们最喜爱的体育项目(每人只选一项)进行了问卷调查,将数据进行了统计并绘制成了如图所示的频数分布直方图和扇形统计图(均不完整).
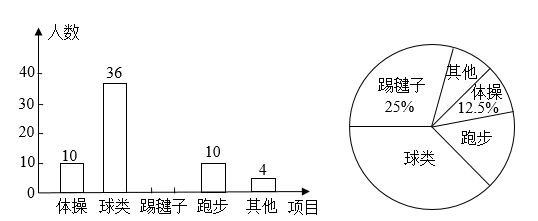 (1)、补全频数分布直方图;(2)、求扇形统计图中表示“跑步”项目扇形圆心角的度数;(3)、根据调查结果,学校准备开展球类比赛,某班要从喜欢球类的甲、乙、丙、丁四位学生中随机抽取两名学生参赛,请列表或画树状图的方法求甲和乙两名学生同时被选中的概率.19. 某学校打算购买甲乙两种不同类型的笔记本. 已知甲种类型的电脑的单价比乙种类型的要便宜10元,且用110元购买的甲种类型的数量与用120元购买的乙种类型的数量一样.(1)、求甲乙两种类型笔记本的单价.(2)、该学校打算购买甲乙两种类型笔记本共100件,且购买的乙的数量不超过甲的3倍,则购买的最低费用是多少?20. 在初中阶段的函数学习中,我们经历了“确定函数的表达式——利用函数图象研究其性质——运用函数解决问题”的学习过程.在画函数图象时,我们通过描点或平移的方法画出了所学的函数图象.同时,我们也学习了绝对值的意义 .
(1)、补全频数分布直方图;(2)、求扇形统计图中表示“跑步”项目扇形圆心角的度数;(3)、根据调查结果,学校准备开展球类比赛,某班要从喜欢球类的甲、乙、丙、丁四位学生中随机抽取两名学生参赛,请列表或画树状图的方法求甲和乙两名学生同时被选中的概率.19. 某学校打算购买甲乙两种不同类型的笔记本. 已知甲种类型的电脑的单价比乙种类型的要便宜10元,且用110元购买的甲种类型的数量与用120元购买的乙种类型的数量一样.(1)、求甲乙两种类型笔记本的单价.(2)、该学校打算购买甲乙两种类型笔记本共100件,且购买的乙的数量不超过甲的3倍,则购买的最低费用是多少?20. 在初中阶段的函数学习中,我们经历了“确定函数的表达式——利用函数图象研究其性质——运用函数解决问题”的学习过程.在画函数图象时,我们通过描点或平移的方法画出了所学的函数图象.同时,我们也学习了绝对值的意义 .结合上面经历的学习过程,现在来解决下面的问题:
在函数中,当时,;当时, .
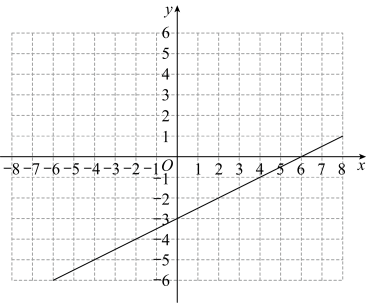 (1)、求这个函数的表达式;(2)、在给出的平面直角坐标系中,请用你喜欢的方法画出这个函数的图象,并写出这个函数的一条性质;(3)、已知函数的图象如图所示,结合你所画的函数图象,直接写出不等式的解集.(4)、若方程有四个不相等的实数根,则实数的取值范围是 .21. 已知和分别切于点B和C,D是上一点,连接 .
(1)、求这个函数的表达式;(2)、在给出的平面直角坐标系中,请用你喜欢的方法画出这个函数的图象,并写出这个函数的一条性质;(3)、已知函数的图象如图所示,结合你所画的函数图象,直接写出不等式的解集.(4)、若方程有四个不相等的实数根,则实数的取值范围是 .21. 已知和分别切于点B和C,D是上一点,连接 .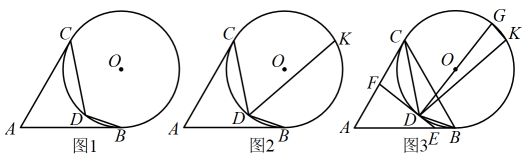 (1)、如图1,求证:;(2)、如图2,作的平分线交于点K,当时,求证:;(3)、如图3,在(2)的条件下,过D的切线分别交于点E,F,作直径 , 连接 , 当F是的中点时, , 求线段的长.22.(1)、【探究发现】
(1)、如图1,求证:;(2)、如图2,作的平分线交于点K,当时,求证:;(3)、如图3,在(2)的条件下,过D的切线分别交于点E,F,作直径 , 连接 , 当F是的中点时, , 求线段的长.22.(1)、【探究发现】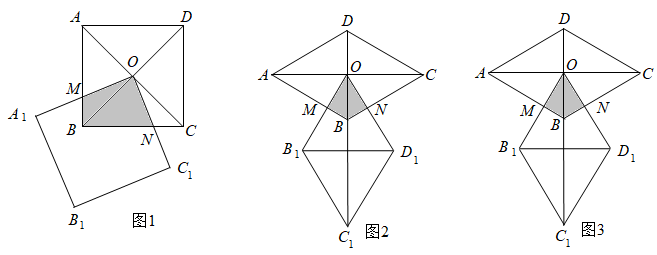
如图1,正方形ABCD两条对角线相交于点O,正方形 与正方形ABCD的边长相等,在正方形 绕点O旋转过程中,边 交边AB于点M,边 交边BC于点N.
①线段BM、BN、AB之间满足的数量关系是;
②四边形OMBN与正方形ABCD的面积关系是 ;
(2)、【类比探究】如图2,若将(1)中的“正方形ABCD”改为“含60°的菱形ABCD”,即 ,且菱形 与菱形ABCD的边长相等.当菱形 绕点O旋转时,保持边 交边AB于点M,边 交边BC于点N.
请猜想:
①线段BM、BN与AB之间的数量关系是 ▲ ;
②菱形OMBN与菱形ABCD的面积关系是 ▲ ;
请你证明其中的一个猜想.
(3)、【拓展延伸】如图3,把(2)中的条件“ ”改为“ ”,其他条件不变,则
① ;(用含α的式子表示)
② . (用含α的式子表示)