2023年深圳市初中学业水平测试数学仿真模拟测试(4)
试卷更新日期:2023-06-06 类型:中考模拟
一、单选题(每题3分,共30分)
-
1. 的倒数是( )A、 B、 C、 D、2. 某零件如图所示,它的俯视图是( )
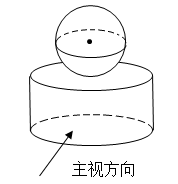 A、
A、 B、
B、 C、
C、 D、
D、 3. 小莹同学10个周综合素质评价成绩统计如下:
3. 小莹同学10个周综合素质评价成绩统计如下:成绩(分)
94
95
97
98
99
100
周数(个)
1
2
2
3
1
1
这 10 个周的综合素质评价成绩的中位数和众数分别是( )
A、97.5 97 B、97 97 C、97.5 98 D、97 984. 第24届冬奥会于2022年2月4日至2月20日在中国北京和张家口成功举办,本届冬奥会的运动员达到2892人,历史规模第二.数据2892用科学记数法表示应是( )A、 B、 C、 D、5. 下列计算正确的是( )A、2a+a=3a2 B、a3•a2=a6 C、a5﹣a3=a2 D、a3÷a2=a6. 不等式组 的解集在数轴上表示为( )A、 B、
B、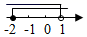 C、
C、 D、
D、 7. 将一把直尺与一块三角板如图放置,若∠1=60°,则∠2为( )
7. 将一把直尺与一块三角板如图放置,若∠1=60°,则∠2为( )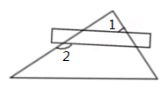 A、150° B、120° C、100° D、60°8. 如图,CE是平行四边形ABCD的边AB的垂直平分线,垂足为点 ,CE与DA的延长线交于点E,连接AC,BE,DO,DO与AC交于点F,则下列结论:①四边形ACBE是菱形;② ;③ ;④S四边形AFOE: ,其中正确的结论有( )
A、150° B、120° C、100° D、60°8. 如图,CE是平行四边形ABCD的边AB的垂直平分线,垂足为点 ,CE与DA的延长线交于点E,连接AC,BE,DO,DO与AC交于点F,则下列结论:①四边形ACBE是菱形;② ;③ ;④S四边形AFOE: ,其中正确的结论有( ) A、①②③ B、①②④ C、①② D、②③④9. 将4个全等的小长方形按如图所示的方式摆放拼成一个大长方形 , 且.设小长方形的宽为 , 长为 , 依题意列二元一次方程组正确的是( )
A、①②③ B、①②④ C、①② D、②③④9. 将4个全等的小长方形按如图所示的方式摆放拼成一个大长方形 , 且.设小长方形的宽为 , 长为 , 依题意列二元一次方程组正确的是( ) A、 B、 C、 D、10. 如图,点A、B、C、D都在 上, , 为 上的一点, , 的延长线交 于 ,若 ,则 的值为( )
A、 B、 C、 D、10. 如图,点A、B、C、D都在 上, , 为 上的一点, , 的延长线交 于 ,若 ,则 的值为( )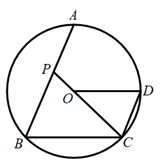 A、2 B、 C、 D、4
A、2 B、 C、 D、4二、填空题(每空3分,共15分)
-
11. 分解因式:﹣9=。
12. 为了估计池塘里有多少条鱼,先从湖里捕捞100条鱼记上标记,然后放回池塘去,经过一段时间,待有标记的鱼完全混合后,第二次再捕捞200条鱼,发现有5条鱼有标记,那么你估计池塘里大约有条鱼.13. 已知关于x的一元二次方程 有两个相等实数根,则m的值为 .14. 如图,在平面直角坐标系中,OB在x轴上,∠ABO=90°,点A的坐标为(2,4),将△AOB绕点A逆时针旋转90°,点O的对应点C恰好落在反比例函数y= 的图象上,则k的值为 .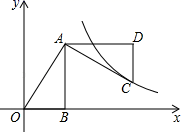 15. 如图,点A在反比例函数y= (x>0)的图象上,点B在反比例函数y= (k<0)的图象上,且OA⊥OB,线段AB交反比例函数y= (x>0) 的图象于另一点C,连结OC。若点C为AB的中点,tan∠OCA= ,则k的值为。
15. 如图,点A在反比例函数y= (x>0)的图象上,点B在反比例函数y= (k<0)的图象上,且OA⊥OB,线段AB交反比例函数y= (x>0) 的图象于另一点C,连结OC。若点C为AB的中点,tan∠OCA= ,则k的值为。
三、解答题(共7题,共55分)
-
16. 计算 sin45°+3tan30°﹣(π﹣1)017. 先化简,再求值: ,其中 .18. 某校为了了解九年级学生(共450人)的身体素质情况,体育老师对九(1)班的50位学生进行一分钟跳绳次数测试,以测试数据为样本,绘制了如下部分频数分布表和部分频数分布直方图.
组别
次数x
频数(人数)
A
80≤x<100
6
B
100≤x<120
8
C
120≤x<140
m
D
140≤x<160
18
E
160≤x<180
6
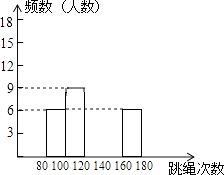
请结合图表解答下列问题:
(1)、表中的m=;(2)、请把频数分布直方图补完整;(3)、这个样本数据的中位数落在第组;(4)、若九年级学生一分钟跳绳次数(x)合格要求是x≥120,则估计九年级学生中一分钟跳绳成绩不合格的人数.19. 神舟十三号飞船即将荣耀归来,为激发同学们对航天事业的兴趣,学校组织进行了一场以“飞天”为主题的文艺晚会,学校打算购买一些“飞天”装饰挂件与专属航天印章送给学生留作纪念.已知每盒挂件有30个,每盒印章有20个,且都只能整盒购买,每盒挂件的价钱比每盒印章的价钱多10元;用200元购买挂件的盒数与用150元购买印章的盒数相同.(1)、求每盒挂件和每盒印章的价格分别为多少元?(2)、如果给每位学生分发2个挂件与2个印章.设购买挂件a盒,购买印章b盒恰好能配套分发,请用含α的代数式表示b;(3)、累计购买超过850元后,超出850元的部分有6折的优惠.学校以(2)中的配套方式购买,共需要花费w元,求w关于a的函数关系式.该校有750名学生,需要购买挂件与印章各多少盒?共需要多少费用?20. 已知二次函数的图象过点 , ,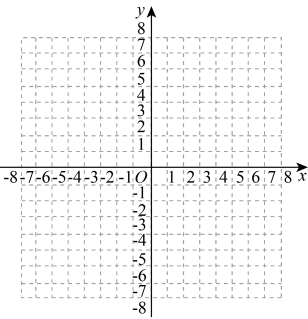 (1)、求此二次函数的解析式并在坐标系内画出其草图;(2)、求直线的解析式;(3)、点M是在第二象限内的该抛物线上,并且三角形的面积为 , 求点M的坐标.(4)、若点P在线段上以每秒一个单位长度的速度从点B向点A运动不与点A,B重合,点P停止运动时点Q随之而停止运动 , 同时,点Q在射线上以每秒个单位的速度从点A向点C运动,设运动时间为t秒,请求出三角形的面积S与t的函数关系式,并求出t为何值时,三角形的面积最大,最大值是多少?21. 如图,圆的内接五边形ABCDE中,AD和BE交于点N,AB和EC的延长线交于点M,CD∥BE,BC∥AD,BM=BC=1,点D是 的中点.
(1)、求此二次函数的解析式并在坐标系内画出其草图;(2)、求直线的解析式;(3)、点M是在第二象限内的该抛物线上,并且三角形的面积为 , 求点M的坐标.(4)、若点P在线段上以每秒一个单位长度的速度从点B向点A运动不与点A,B重合,点P停止运动时点Q随之而停止运动 , 同时,点Q在射线上以每秒个单位的速度从点A向点C运动,设运动时间为t秒,请求出三角形的面积S与t的函数关系式,并求出t为何值时,三角形的面积最大,最大值是多少?21. 如图,圆的内接五边形ABCDE中,AD和BE交于点N,AB和EC的延长线交于点M,CD∥BE,BC∥AD,BM=BC=1,点D是 的中点. (1)、求证:BC=DE;(2)、求证:AE是圆的直径;(3)、求圆的面积.22. 如图1,点E是正方形ABCD外的一点,以DE为边构造正方DEFG,点M是△ADE边AE上的动点,点N是△CDG的边CG上的动点.
(1)、求证:BC=DE;(2)、求证:AE是圆的直径;(3)、求圆的面积.22. 如图1,点E是正方形ABCD外的一点,以DE为边构造正方DEFG,点M是△ADE边AE上的动点,点N是△CDG的边CG上的动点. (1)、证明:△ADE≌△CDG;(2)、如图(1):当DM和DN分别是△ADE和△CDG的中线时,试猜想DM和DN的数量关系和位置关系,并说明理由;(3)、类比猜想:
(1)、证明:△ADE≌△CDG;(2)、如图(1):当DM和DN分别是△ADE和△CDG的中线时,试猜想DM和DN的数量关系和位置关系,并说明理由;(3)、类比猜想:①在(2)问中,当DM、DN分别是△ADE和△CDG的高(如图2),其他条件不变时,问题(2)的结论是否仍然成立?(只写出结论,不要求证明)
②在(2)问中,当DM、DN分别是△ADE和△CDG的角平分线,其他条件不变时,问题(2)的结论是否仍然成立?(只写出结论,不要求证明)