2023年深圳市初中学业水平测试数学仿真模拟测试(1)
试卷更新日期:2023-06-06 类型:中考模拟
一、单选题(每题3分,共30分)
-
1. 若a与2互为倒数,则下列判断正确的是( ).A、a+2=0 B、a-2=0 C、2a=0 D、2a=12. 如图,将小立方块①从4个大小相同的小立方块所搭几何体中移走后,所得几何体( )
 A、俯视图改变,左视图改变 B、俯视图不变,左视图改变 C、主视图改变,左视图不变 D、主视图不变,左视图不变3. 某篮球队16名队员的年龄情况如下表,则这些队员年龄的众数和中位数分别是( )
A、俯视图改变,左视图改变 B、俯视图不变,左视图改变 C、主视图改变,左视图不变 D、主视图不变,左视图不变3. 某篮球队16名队员的年龄情况如下表,则这些队员年龄的众数和中位数分别是( )年龄(单位:岁)
14
15
16
17
18
人数
3
3
5
3
2
A、16,17 B、16,16 C、16,16.5 D、3,174. 面对2020年突如其来的新冠疫情,党和国家及时采取应对措施,投入大量资金进行新冠疫苗的研究.据统计共投入约57亿元资金.57亿用科学记数法可表示为( )A、 B、 C、 D、5. 下列计算正确的是( )A、 B、 C、 D、6. 不等式组的解集是( )A、﹣2≤x<1 B、﹣2≤x<2 C、﹣8≤x<1 D、﹣2≤x或x>27.如图,将一副三角板和一张对边平行的纸条按下列方式摆放,两个三角板的一直角边重合,含30°角的直角三角板的斜边与纸条一边重合,含45°角的三角板的一个顶点在纸条的另一边上,则∠1的度数是( )
 A、30° B、20° C、15° D、14°8. 要检验一个四边形的桌面是矩形,可行的测量方案是( )A、任选两个角,测量它们的角度 B、测量四条边的长度 C、测量两条对角线的长度 D、测量两条对角线的交点到四个顶点的距离9. 将4个全等的小长方形按如图所示的方式摆放拼成一个大长方形 , 且.设小长方形的宽为 , 长为 , 依题意列二元一次方程组正确的是( )
A、30° B、20° C、15° D、14°8. 要检验一个四边形的桌面是矩形,可行的测量方案是( )A、任选两个角,测量它们的角度 B、测量四条边的长度 C、测量两条对角线的长度 D、测量两条对角线的交点到四个顶点的距离9. 将4个全等的小长方形按如图所示的方式摆放拼成一个大长方形 , 且.设小长方形的宽为 , 长为 , 依题意列二元一次方程组正确的是( ) A、 B、 C、 D、10.
A、 B、 C、 D、10.一个边长为4的等边三角形ABC的高与⊙O的直径相等,如图放置,⊙O与BC相切于点C,⊙O与AC相交于点E,则CE的长是( )
 A、 B、 C、2 D、3
A、 B、 C、2 D、3二、填空题(每空3分,共15分)
-
11. 分解因式: .12. 某人工养殖池塘共有草鱼5000条和其它鱼类若干条,几次随机打捞中共捕获鱼300条,其中草鱼150条,试估计池塘中共养殖鱼条.13. 请填写一个常数,使得关于的方程有两个不相等的实数根.14. 如图,在YABCD中,E为BC边上一点,且AB=AE,若AE平分∠DAB,∠EAC=25°,则∠AED的度数是度.
 15. 如图,在面积为80 cm²的矩形ABCD中作等边△BEF,点E,F分别落在AD,BC上,将△BEF向右平移得到△B1E1F1(点B1在F的左侧),再将△B1E1F1向右平移,使得F1与C重合,得到△B2E2C(点B2在F1的左侧),且第二次平移的距离是第一次平移距离的1.4倍.若FB2= BE,则阴影部分面积为cm²。
15. 如图,在面积为80 cm²的矩形ABCD中作等边△BEF,点E,F分别落在AD,BC上,将△BEF向右平移得到△B1E1F1(点B1在F的左侧),再将△B1E1F1向右平移,使得F1与C重合,得到△B2E2C(点B2在F1的左侧),且第二次平移的距离是第一次平移距离的1.4倍.若FB2= BE,则阴影部分面积为cm²。
三、解答题(共7题,共55分)
-
16.(1)、计算:(2)、解方程:x2-2x-1=017. 先化简,再求代数式 的值,其中m=2cos30°-tan45°18. 疫情期间,游海中学进行了一次线上数学学情调查,九(1)班数学李老师对成绩进行分析,制作如下的频数分布表和频数分布直方图.60到70之间学生成绩尚未统计,根据情况画出的扇形图如图.请解答下列问题:
类别
分数段
频数(人数)
A
a
B
16
C
24
D
6
 (1)、完成频数分布表,a= ▲ , B类圆心角= ▲ °,并补全频数分布直方图;(2)、全校九年级共有720名学生全部参加此次测试,估计该校成绩范围内的学生有多少人?(3)、九(1)班数学老师准备从D类优生的6人中随机抽取两人进行线上学习经验交流,已知这6人中有两名是无家长管理的留守学生,求恰好只选中其中一名留守学生进行经验交流的概率.19. 为贯彻执行“德、智、体、美、劳”五育并举的教育方针,内江市某中学组织全体学生前往某劳动实践基地开展劳动实践活动.在此次活动中,若每位老师带队30名学生,则还剩7名学生没老师带;若每位老师带队31名学生,就有一位老师少带1名学生.现有甲、乙两型客车,它们的载客量和租金如表所示:
(1)、完成频数分布表,a= ▲ , B类圆心角= ▲ °,并补全频数分布直方图;(2)、全校九年级共有720名学生全部参加此次测试,估计该校成绩范围内的学生有多少人?(3)、九(1)班数学老师准备从D类优生的6人中随机抽取两人进行线上学习经验交流,已知这6人中有两名是无家长管理的留守学生,求恰好只选中其中一名留守学生进行经验交流的概率.19. 为贯彻执行“德、智、体、美、劳”五育并举的教育方针,内江市某中学组织全体学生前往某劳动实践基地开展劳动实践活动.在此次活动中,若每位老师带队30名学生,则还剩7名学生没老师带;若每位老师带队31名学生,就有一位老师少带1名学生.现有甲、乙两型客车,它们的载客量和租金如表所示:甲型客车
乙型客车
载客量(人/辆)
35
30
租金(元/辆)
400
320
学校计划此次劳动实践活动的租金总费用不超过3000元.
(1)、参加此次劳动实践活动的老师和学生各有多少人?(2)、每位老师负责一辆车的组织工作,请问有哪几种租车方案?(3)、学校租车总费用最少是多少元?20. 如图1,在平面直角坐标系中,已知点A,B的坐标分别为 和 ,点E为x轴正半轴上的一个动点,过点A、B、E作 的外接圆 ,连结 并延长交圆于点D,连结 、 .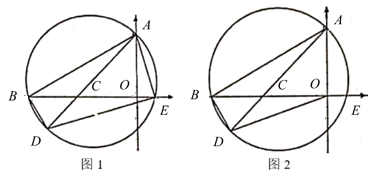 (1)、求证: .(2)、当 时,求 的长度.(3)、如图2,连结 ,求线段 的最小值及当 最小时 的外接圆圆心C的坐标.21. 在平面直角坐标系中,抛物线(m是常数)的顶点为A.(1)、用含m的代数式表示抛物线L的对称轴.(2)、当 , 抛物线L的最高点的纵坐标为6时,求抛物线L对应的函数表达式.(3)、已知点、 , 当时,设的面积为S.求S与m之间的函数关系式,并求S的最小值.(4)、已知矩形MNPQ的四个顶点的坐标分别为、、、 , 当抛物线L与边MN、PQ各有1个交点分别为点D、E时,若点D到y轴的距离和点E到x轴的距离相等,直接写出m的值.22.(1)、【探究发现】如图①所示,在正方形中,为边上一点,将沿翻折到处,延长交边于点.求证:
(1)、求证: .(2)、当 时,求 的长度.(3)、如图2,连结 ,求线段 的最小值及当 最小时 的外接圆圆心C的坐标.21. 在平面直角坐标系中,抛物线(m是常数)的顶点为A.(1)、用含m的代数式表示抛物线L的对称轴.(2)、当 , 抛物线L的最高点的纵坐标为6时,求抛物线L对应的函数表达式.(3)、已知点、 , 当时,设的面积为S.求S与m之间的函数关系式,并求S的最小值.(4)、已知矩形MNPQ的四个顶点的坐标分别为、、、 , 当抛物线L与边MN、PQ各有1个交点分别为点D、E时,若点D到y轴的距离和点E到x轴的距离相等,直接写出m的值.22.(1)、【探究发现】如图①所示,在正方形中,为边上一点,将沿翻折到处,延长交边于点.求证: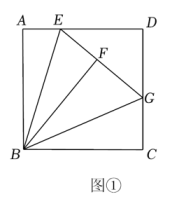 (2)、【类比迁移】如图②,在矩形中,为边上一点,且将沿翻折到处,延长交边于点延长交边于点且求的长.
(2)、【类比迁移】如图②,在矩形中,为边上一点,且将沿翻折到处,延长交边于点延长交边于点且求的长. (3)、【拓展应用】如图③,在菱形中,为边上的三等分点,AB=6,将沿翻折得到 , 直线交于点求的长.
(3)、【拓展应用】如图③,在菱形中,为边上的三等分点,AB=6,将沿翻折得到 , 直线交于点求的长.