2023年北师大版数学七年级下学期期末模拟试卷（5）

试卷更新日期：2023-06-06 类型：期末考试

进入出卷网下载

一、单选题（每题3分，共30分）

1. 下面是沈阳、大连、青岛、济南四个城市的地铁图标，其中是轴对称图形的是（）

A、 B、 C、 D、

查看试题解析
2. 在研制新冠肺炎疫苗中，某细菌的直径大小为0.000000072毫米，用科学记数法表示这一数字为（）

A、 $7.2 \times 1 0^{- 7}$ B、 $0.72 \times 1 0^{- 7}$ C、 $7.2 \times 1 0^{- 8}$ D、 $7.2 \times 1 0^{- 9}$

查看试题解析
3. 下列各式中，计算正确的是（）

A、 $a^{6} + a^{6} = 2 a^{12}$ B、 $a^{8} \div a^{2} = a^{4}$ C、 $a^{3} \cdot a^{2} = a^{6}$ D、 $a^{3} \cdot {(- a)}^{5} \cdot a^{12} = - a^{20}$

查看试题解析
4. 如图，下列能判定 $A B ∥ C D$ 的条件是（）．

A、 $∠ B + ∠ B A D = 180 °$ B、 $∠ 1 = ∠ 2$ C、 $∠ 3 = ∠ 4$ D、 $∠ D = ∠ 5$

查看试题解析
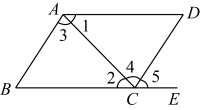5. 用直尺和圆规作一个角等于已知角，如图，要证 $∠ A^{'} O^{'} B^{'} = ∠ A O B$ ，则只需证明 $△ O D C ≌ △ O^{'} D^{'} C^{'}$ ，依据是（）

A、SAS B、SSS C、AAS D、ASA

查看试题解析
6. 下列说法错误的是（）

A、“从一个只有红球的袋子里面摸出一个球是红球”是必然事件 B、如果明天降水的概率是 $50 %$ ，那么明天有半天都在降雨 C、“随意掷两个均匀的骰子，朝上面的点数之和为13”是不可能事件 D、随机事件发生的概率介于 $0$ 和 $1$ 之间

查看试题解析
7. 如图．已知直线 $a ∥ b$ ，将一块含 $30 °$ 角的直角三角板ABC按如图方式放置（ $∠ A C B = 30 °$ ）其中点A，B分别落在直线a、b上．若 $∠ 1 = 46 °$ ，则 $∠ 2$ 的度数为（）

A、 $23 °$ B、 $44 °$ C、 $46 °$ D、 $54 °$

查看试题解析
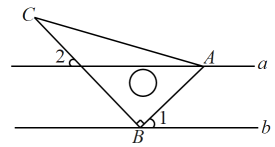8. 下列说法中，正确的个数为（）
①三角形的高、中线、角平分线都是线段②三角形的外角大于任意一个内角③△ABC中，∠A＝2∠B＝3∠C，则△ABC是直角三角形④若a、b、c均大于0，且满足a+b＞c，则长为a、b、c的三条线段一定能组成三角形

A、1 B、2 C、3 D、4

查看试题解析
9. 如图，向高为H的圆柱形空水杯中注水，表示注水量ｙ与水深ｘ的关系的图象是下面哪一个？（）

A、 B、 C、 D、

查看试题解析
10. 如图，在 $△ A B C$ 与 $△ A E F$ 中， $A B = A E$ ， $B C = E F$ ， $∠ A B C = ∠ A E F$ ， $∠ E A B = 40 °$ ， $A B$ 交 $E F$ 于点 $D$ ，连接 $E B .$ 下列结论：① $∠ F A C = 40 °$ ；② $A F = A C$ ；③ $∠ E F B = 40 °$ ；④ $A D = A C$ ，正确的个数为（）

A、 $1$ 个 B、 $2$ 个 C、 $3$ 个 D、 $4$ 个

查看试题解析

二、填空题（每空3分，共15分）

11. $202 2^{2} - 2021 \times 2023 =$ ．

查看试题解析
12. 长度分别为3cm，4cm，5cm，9cm的四条线段，任取其中三条能组成三角形的概率是．

查看试题解析
13. 如图所示的计算程序中，y与x之间的关系式是．

查看试题解析
14. (-4)²⁰²²×(0.25)²⁰²³= ．

查看试题解析
15. 如图， $C D$ 是 $△ A B C$ 的中线，延长 $C D$ 至点E，使 $C E = \frac{5}{4} C D$ .连接 $A E$ 并延长，交 $C B$ 的延长线于点F，已知四边形 $B D E F$ 的面积为2，则 $△ A F C$ 的面积是.

查看试题解析

三、解答题（共7题，共55分）

16.

(1)、计算： ${(- 2)}^{- 4} \times {(- \frac{1}{2})}^{- 3} - {(\sqrt{2} - 1)}^{0} + {(\frac{1}{2})}^{- 1}$ ；

(2)、计算： $(8 m^{2} n) \cdot (- 2 m n) \div (4 m n^{2})$ ．

查看试题解析
17. 先化简，再求值： $(2 x + 5) (2 x - 5) + {(x - 3)}^{2} - 6 x (x - 1)$ ，其中 $x = 6$ .

查看试题解析
18. 完成下面的证明过程.
已知：如图， $A B / / C D ， A E ⊥ B D$ 于 $E ， C F ⊥ B D$ 于 $F ， B F = D E$ .

求证： $△ A B E ≅ △ C D F$ .

证明： $∵ A B / / C D ， ∴ ∠ 1 =$ ▲ (两直线平行，内错角相等).

$∵ A E ⊥ B D ， C F ⊥ B D$ ，

$∴ ∠ A E B =$ ▲ $= 90^{\circ}$

$∵ B F = D E$ ，

$∴ B E =$ ▲

在 $△ A B E$ 和 $△ C D F$ 中， ${\begin{cases} ∠ 1 =_____ \\ B E =_____ \\ ∠ A E B =_____ \end{cases}$

$∴ △ A B E ≅ △ C D F$ （）.

查看试题解析
19. 小明家里的阳台地面，水平铺设了仅黑白颜色不同的18块方砖（如图），他从房间里向阳台抛小皮球，小皮球最终随机停留在某块方砖上．

(1)、求小皮球分别停留在黑色方砖与白色方砖上的概率；

(2)、上述哪个概率较大？要使这两个概率相等，应改变第几行第几列的哪块方砖颜色？怎样改变？

查看试题解析
20. 在平面直角坐标系中， $D (0 ， a)$ ， $M (b ， a)$ ，满足 $\sqrt{a + 3} + | b - 4 | = 0$ ， $△ A B C$ 中 $∠ A C B = 90 °$ ， $△ A B C$ 的边与 $x$ 轴分别交于 $O$ 、 $G$ 两点，与直线 $D M$ 分别交于 $E$ 、 $F$ 两点．

(1)、求 $a =$ ； $b =$ ．

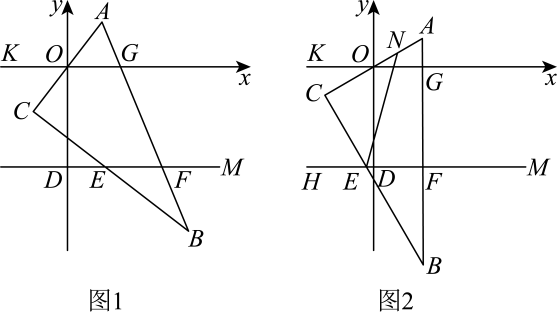(2)、将直角三角形 $A B C$ 如图1位置摆放，求证： $∠ K O C + ∠ C E D = 90 °$ ；

(3)、将直角三角形 $A B C$ 如图2位置摆放， $N$ 为 $A C$ 上一点， $∠ N E F + ∠ C E F = 180 °$ ，请写 $∠ N E F$ 与 $∠ A O G$ 之间的等量关系，并说明理由

查看试题解析
21. 如图①是一个长为 $2 a$ 、宽为 $2 b$ 的长方形，沿图中虚线用剪刀均分成四块小长方形，然后按图②的形状拼成一个正方形．

(1)、观察图②．请你直接写出下列三个式子： ${(a + b)}^{2}$ ， ${(a - b)}^{2}$ ， $4 a b$ 之间的等量关系式为；

(2)、若m、n均为实数，且 $m + n = - 2$ ， $m n = - 3$ ，运用（1）所得到的公式求 $m - n$ 的值；

(3)、如图③， $S_{1}$ ， $S_{2}$ 分别表示边长为x、y的正方形的面积，且A、B、C三点在一条直线上，若 $S_{1} + S_{2} = 20$ ， $A B = x + y = 6$ ，求图中阴影部分的面积．

查看试题解析
22. 第一学习小组按照老师留的预习任务，对如下问题进行了自主探究性学习：
已知：如图1所示，在 $△ A B C$ 中， $C A = C B$ ， $∠ A C B = 90 °$ ， $A D$ 是 $△ A B C$ 的中线，过点C作 $C E ⊥ A D$ ，垂足为M，且交 $A B$ 于点E．

(1)、【探究一：相等的角】
同学们用量角器度量后猜想 $∠ B C E = ∠ C A D$ ，请你先判断他们的猜想是否符合题意，再用所学知识说明理由；

(2)、【探究二：相等的线段】
如图2所示，组员小亮在（1）的条件上添加了一条线段 $C N$ ，且 $C N$ 平分 $∠ A C B$ 交 $A D$ 于点N，即可得 $C N = B E$ ，并给出了说明理由；请你和他共同完成下面的说理过程．
解：如图2中，
因为 $C N$ 平分 $∠ A C B$ ， $∠ A C B = 90 °$ ，
所以 $∠ A C N = \frac{1}{2} ∠ A C B = 45 °$ ，（依据：       ）
因为 $C A = C B$ ，
所以 $∠ B = 45 °$ ，
所以 $∠ A C N = ∠ B$ ，
在 $△ A C N$ 和 $△ C B E$ 中，
因为▲ ， ▲ ， ▲
所以 $△ A C N ≌ △ C B E$ （依据：       ），
所以 $C N = B E$ ．（依据：      ）

(3)、【探究三：全等的三角形】
如图3所示，组员小刚在（2）的条件上，连接 $D E$ ，又发现了一组全等三角形，请直接写出这组全等三角形．

查看试题解析