浙江省温州市文成县2022-2023学年七年级下学期期中数学试卷

试卷更新日期：2023-06-06 类型：期中考试

进入出卷网下载

一、选择题（本大题共10小题，共30.0分。在每小题列出的选项中，选出符合题目的一项）

1.
如图，∠1的内错角是（　　）

A、∠2 B、∠3 C、∠4 D、∠5

查看试题解析
2. 下列方程中，属于二元一次方程的是（）

A、 $6 x - 2 z = 5 y$ B、 $\frac{1}{x} + \frac{1}{y} = 5$ C、 $x^{2} - 3 y = 1$ D、 $x - 2 y = 3$

查看试题解析
3. 计算 $t^{6} \cdot t^{2}$ 的结果是（）

A、 $t^{12}$ B、 $2 t^{8}$ C、 $t^{8}$ D、 $t^{4}$

查看试题解析
4. 已知新型冠状病毒的直径约为 $0.00015$ 毫米，那么用科学记数法可表示为（）

A、 $1.5 \times 10^{- 4}$ 毫米 B、 $1.5 \times 10^{4}$ 毫米 C、 $1.5 \times 10^{- 5}$ 毫米 D、 $1.5 \times 10^{5}$ 毫米

查看试题解析
5. 下列整式乘法运算中，正确的是（）

A、 $(a + 1) (a - 2) = a^{2} - 2$ B、 $(a + 2) (a - 2) = a^{2} - 2$ C、 ${(a + 1)}^{2} = a^{2} + 1$ D、 $(a - b) (a + b) = a^{2} - b^{2}$

查看试题解析
6. 用加减消元法解二元一次方程组 ${\begin{array}{l} x + 3 y = 4 ① \\ 2 x - y = 1 ② \end{array}$ 时，下列方法中无法消元的是（）

A、 $① \times 2 - ②$ B、 $① \times (- 2) + ②$ C、 $① - ② \times 3$ D、 $① + ② \times 3$

查看试题解析
7. 如图所示，直线 $a / / b$ ，直角 $△ A B C$ 的顶点 $C$ 在直线 $b$ 上.若 $∠ 1 = 33 °$ ，则 $∠ 2$ 的度数为（）

A、 $57 °$ B、 $47 °$ C、 $67 °$ D、 $33 °$

查看试题解析
8. 若多项式 $x^{2} + k x + 16$ 是一个完全平方式，则 $k$ 的值应是（）

A、 4或-4 B、8 C、-8 D、8或-8

查看试题解析
9. 某班共有40位学生.近期由于诺如病毒感染，该班有一位男生因病请假，当天的男生人数恰为女生人数的一半.若设该班男生人数为 $x$ ，女生人数为 $y$ ，则依题意列二元一次方程组正确的是（）

A、 ${\begin{array}{l} x + y = 40 \\ y = 2 (x + 1) \end{array}$ B、 ${\begin{array}{l} x + y = 40 \\ y = 2 (x - 1) \end{array}$ C、 ${\begin{array}{l} x - y = 40 \\ y = 2 (x + 1) \end{array}$ D、 ${\begin{array}{l} x - y = 40 \\ y = 2 (x - 1) \end{array}$

查看试题解析
10. 若 $(x - m) (x - n) = x^{2} + 2 x - 4$ ，则代数式 ${(m n)}^{(m + n)}$ 的值为（）

A、 8 B、 $\frac{1}{8}$ C、16 D、 $\frac{1}{16}$

查看试题解析

二、填空题（本大题共8小题，共24.0分）

11. 计算：（a³）²= ．

查看试题解析
12. 若 ${\begin{array}{l} x = 2 \\ y = 1 \end{array}$ 是关于 $x$ 、 $y$ 的方程 $2 x + a y = 6$ 的解，则 $a$ 的值为．

查看试题解析
13. 已知 $x - 2 y = 10$ ，用含 $y$ 代数式表示 $x$ ，则 $x =$ ．

查看试题解析
14. 一个长方形的面积为 $6 a^{2} b - 9 a b$ ，已知这个长方形的长为 $3 a b$ ，则宽为．

查看试题解析
15. 如图，将周长为 $10 c m$ 的 $△ A B C$ 沿射线 $B C$ 方向平移 $2 c m$ 后得到 $△ D E F$ ，则四边形 $A B F D$ 的周长为 $c m$ ．

查看试题解析
16. 已知方程组 ${\begin{array}{l} 3 x + 2 y = 2 m \\ 2 x + y = 1 \end{array}$ ，当 $m =$ 时， $x + y = 5$ ．

查看试题解析
17. 如图，在长方形 $A B C D$ 中，点 $E$ 、 $F$ 分别是线段 $B C$ 、 $A D$ 上的两点，点 $G$ 是线段 $F D$ 上的一点，连结 $E F$ ， $E G$ .将四边形 $C D G E$ 沿着 $E G$ 折叠，得到四边形 $C' D' G E$ .已知 $∠ F E G = 35 °$ ，若 $E F$ 恰好平分 $∠ C' E G$ ，则 $∠ E F G$ 的度数是度.

查看试题解析
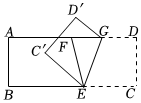18. 小文在拼图时，发现8个一样大小的长方形，恰好可以拼成一个大的长方形如图（1）；小成看见了，说：“我也来试一试”.结果小成七拼八凑，拼成了如图（2）那样的正方形，中间还留下了一个面积为 $4 m m^{2}$ 的小正方形缺口，则每个小长方形的周长为 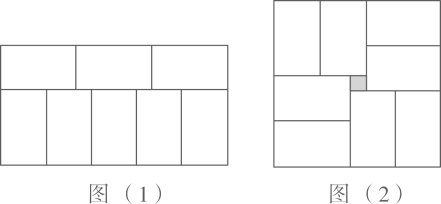$m m$ ．

查看试题解析

三、解答题（本大题共6小题，共46.0分。解答应写出文字说明，证明过程或演算步骤）

19. 计算：

(1)、 ${(- 1)}^{2023} + {(3.14 - π)}^{0} + {(2)}^{- 2}$

(2)、 ${(2 x)}^{2} - x^{3} \div x + x^{2}$

查看试题解析
20. 解下列二元一次方程组：

(1)、 ${\begin{array}{l} y = 2 x \\ 3 x - y = 1 \end{array}$

(2)、 ${\begin{array}{l} 2 x - 3 y = 7 \\ 4 x + 5 y = 3 \end{array}$

查看试题解析
21. 阅读下列推理过程，在括号中填写理由．
如图，已知 $A D ⊥ B C$ ， $∠ C F E = 90 °$ ， $∠ 1 + ∠ 2 = 180 °$ ．

试说明： $∠ B = ∠ C D G$ ．

解： $∵ A D ⊥ B C$ （已知），

$∴ ∠ A D B = 90 °$ （垂直的意义）．

$∵ ∠ C F E = 90 °$ （已知），

$∴ ∠ A D B + ∠ C F E = 180 °$ ．

$∴ A D / / E F$ （        ）.

$∴ ∠ 2 +$ ▲ $= 180 °$ ．

$∵ ∠ 1 + ∠ 2 = 180 °$ （已知），

$∴ ∠ 1 =$ ▲（        ）.

$∴ D G / / B A$ ，

$∴ ∠ B = ∠ C D G$ （        ）.

查看试题解析
22. 先化简，再求值： $- 4 b^{2} + {(a + 2 b)}^{2} - a (a - b)$ ，其中 $a = - 3$ ， $b = \frac{1}{5}$ ．

查看试题解析
23. 如图，已知 $F$ ， $E$ 分别是射线 $A B$ ， $C D$ 上的点.连接 $A C$ ， $A E$ 平分 $∠ B A C$ ， $E F$ 平分 $∠ A E D$ ， $∠ 2 = ∠ 3$ ．

(1)、试说明 $A B / / C D$ ；

(2)、若 $∠ A F E - ∠ 2 = 30 °$ ，求 $∠ A F E$ 的度数．

查看试题解析

24. 根据以下素材，探索完成任务．

如何设计板材裁切方案？
素材1	图1中是一张学生椅，主要由靠背、座垫及铁架组成.测量，该款学生椅的靠背尺寸为 $40 c m \times 15 c m$ ，座垫尺寸为 $40 c m \times 35 c m$ .图2是靠背与座垫的尺寸示意图．
素材2	因学校需要，某工厂配合制作该款式学生椅.经清点库存时发现，工厂仓库已有大量的学生椅铁架，只需在市场上购进某型号板材加工制做该款式学生椅的靠背与座垫.已知该板材长为 $240 c m$ ，宽为 $40 c m$ .（裁切时不计损耗）
我是板材裁切师
任务一	拟定裁切方案	若要不造成板材浪费，请你设计出一张该板材的所有裁切方法．方法一：裁切靠背16张和座垫0张．方法二：裁切靠背张和坐垫张. 方法三：裁切靠背张和坐垫张.
任务二	确定搭配数量	若该工厂购进50张该型号板材，能制作成多少张学生椅？
任务三	解决实际问题	现需要制作700张学生椅，该工厂仓库现有1张座垫和11张靠背，还需要购买该型号板材多少张（恰好全部用完）？并给出一种裁切方案．

查看试题解析