浙江省温州市文成县2022-2023学年八年级下学期期中数学试卷
试卷更新日期:2023-06-06 类型:期中考试
一、选择题(本大题共10小题,共30.0分。在每小题列出的选项中,选出符合题目的一项)
-
1. 要使二次根式有意义,则应满足下面哪个选项( )A、 B、. C、 D、2. 下列运算正确的是( )A、 B、 C、 D、3. 一个多边形内角和度数为 , 则这个多边形边数为( )A、 B、 C、 D、4. 一组数据 , , , , , 则这组数据的中位数是( )A、 B、 C、 D、5. 如图,为了保证铁路的两条直铺的铁轨互相平行,只要使互相平行的夹在铁轨之间的枕木长相等就可以了,依据是:两条铁轨和夹在铁轨之间的两根枕木构成一个平行四边形,即可得到两条铁轨平行.判定铁轨和枕木构成平行四边形的依据是( )
 A、 平行线间的距离处处相等 B、一组对边平行且相等的四边形是平行四边形 C、两组对边分别相等的四边形是平行四边形 D、两组对边分别平行的四边形是平行四边形6. 用配方法解方程 , 将其化为的形式,正确的是( )A、 B、 C、 D、7. 关于的方程的根的情况为( )A、 有两个不相等的实数根 B、有两个相等的实数根 C、没有实数根 D、由的取值决定8. 如图,平行四边形中,点为对角线的中点,直线经过点分别与 , 交于点 , , 下列结论中,不一定成立的是( )
A、 平行线间的距离处处相等 B、一组对边平行且相等的四边形是平行四边形 C、两组对边分别相等的四边形是平行四边形 D、两组对边分别平行的四边形是平行四边形6. 用配方法解方程 , 将其化为的形式,正确的是( )A、 B、 C、 D、7. 关于的方程的根的情况为( )A、 有两个不相等的实数根 B、有两个相等的实数根 C、没有实数根 D、由的取值决定8. 如图,平行四边形中,点为对角线的中点,直线经过点分别与 , 交于点 , , 下列结论中,不一定成立的是( )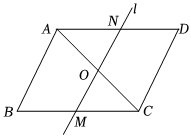 A、 B、 C、 D、9. 在△ABC中,∠ABC=90°, AB=6cm,BC=8cm,动点P从点A沿线段AB向点B移动,一动点Q从点B沿线段BC向点C移动,两点同时开始移动,点P的速度为1cm/s,点Q的速度为2cm/s,当Q到达点C时两点同时停止运动.若使△PBQ的面积为5cm2 , 则点P运动的时间是( )A、1s B、4s C、5s或1s D、4s或1s10. 如图,已知▱的顶点 , , 点在轴正半轴上,按以下步骤作图:①以点为圆心,适当长度为半径作弧,分别交边 , 于点 , ;②分别以点 , 为圆心,大于的长为半径作弧,两弧在内交于点;③作射线 , 交边于点 , 则点的坐标为( )
A、 B、 C、 D、9. 在△ABC中,∠ABC=90°, AB=6cm,BC=8cm,动点P从点A沿线段AB向点B移动,一动点Q从点B沿线段BC向点C移动,两点同时开始移动,点P的速度为1cm/s,点Q的速度为2cm/s,当Q到达点C时两点同时停止运动.若使△PBQ的面积为5cm2 , 则点P运动的时间是( )A、1s B、4s C、5s或1s D、4s或1s10. 如图,已知▱的顶点 , , 点在轴正半轴上,按以下步骤作图:①以点为圆心,适当长度为半径作弧,分别交边 , 于点 , ;②分别以点 , 为圆心,大于的长为半径作弧,两弧在内交于点;③作射线 , 交边于点 , 则点的坐标为( )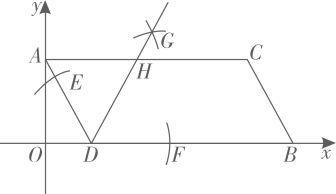 A、 B、 C、 D、
A、 B、 C、 D、二、填空题(本大题共8小题,共24.0分)
-
11. 用反证法证明命题“在同一平面内,若a⊥b,c⊥b,则a//c”时,首先应假设 .12. 点关于原点的对称点的坐标为 .13. 如果实数、满足 , 那么的值为 .14. 己如实数m是方程的一个根,则代数式的值为 .15. 某企业决定招聘广告策划人员一人,某应聘者三项素质测试的成绩(单位:分)如下:
测试项目
创新能力
综合知识
语言表达
测试成绩
如果将创新能力、综合知识和语言表达三项素质测试成绩按::的比确定应聘者的最终成绩,则该应聘者的最终成绩为分.
16. 如图,在中,点 , 分别为 , 的中点,平分 , 交于点 , 连接并延长交于 , 已知 , , , 则 . 17. 如图,在平行四边形中, , , 将沿翻折得到 , 交于点 , , 则的长度为 .
17. 如图,在平行四边形中, , , 将沿翻折得到 , 交于点 , , 则的长度为 .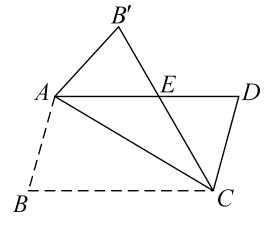 18. 气动升降桌由于高度可调节,给人们学习生活带来许多便捷.如图1所示是桌子的侧平面示意图, , , , , 是固定钢架,垂直桌面 , 是位置可变的定长钢架.是两端固定的伸缩杆,其中, , , , 是一个固定角为 , 当旋转至水平位置时,伸缩杆最短,此时伸缩杆的长度为点的离地高度为 , , 小南将桌子调整到他觉得最舒服的高度,此时发现 , 则桌面高度为 .
18. 气动升降桌由于高度可调节,给人们学习生活带来许多便捷.如图1所示是桌子的侧平面示意图, , , , , 是固定钢架,垂直桌面 , 是位置可变的定长钢架.是两端固定的伸缩杆,其中, , , , 是一个固定角为 , 当旋转至水平位置时,伸缩杆最短,此时伸缩杆的长度为点的离地高度为 , , 小南将桌子调整到他觉得最舒服的高度,此时发现 , 则桌面高度为 .
三、解答题(本大题共6小题,共46.0分。解答应写出文字说明,证明过程或演算步骤)
-
19.(1)、计算:;(2)、解方程: .20. 如图,在的网格中,每个小正方形的边长都是1,点 , , 均在格点上.
 (1)、在图1中,作一个各顶点均在格点上的▱ , 使得为对角线交点;(2)、在图2中,作一个各顶点均在格点上的▱ , 使其面积等于8,且该平行四边形的一条边等于其一条对角线.21. 如图,在平行四边形中,、分别是边、的一点,且 , 连接、求证:四边形是平行四边形.
(1)、在图1中,作一个各顶点均在格点上的▱ , 使得为对角线交点;(2)、在图2中,作一个各顶点均在格点上的▱ , 使其面积等于8,且该平行四边形的一条边等于其一条对角线.21. 如图,在平行四边形中,、分别是边、的一点,且 , 连接、求证:四边形是平行四边形. 22. 近年来网的车给人们的出行带来了便利,小明和数学兴趣小组的同学对甲、乙两家曾康会司司机月收入进行了描样调查,两家公司分别抽取的名司机月收入(单位:千元)如图所示:
22. 近年来网的车给人们的出行带来了便利,小明和数学兴趣小组的同学对甲、乙两家曾康会司司机月收入进行了描样调查,两家公司分别抽取的名司机月收入(单位:千元)如图所示:
根据以上信息,整理分析数据如下:
平均月收入千元
中位数
众数
方差
甲公司
乙公司
(1)、填空; , , , .(2)、小明的叔叔计划从两家公司中选择一家做网约车司机,如果你是小明,你建议他选哪家公司?请说明理由23. 如图,某游乐场游客中心位于处,其正南方向米处有海盗船游乐项目 , 在的正东方向米处有摩天轮游乐项目餐厅位于的中点;碰碰车游乐项目位于上,且恰好处于餐厅的正南方向小快从出发,经到匀速骑行游玩,曼曼同时从出发,沿南偏西方向匀速直线行走游玩.(1)、餐厅和碰碰车游乐项目相距多少米?(2)、已知小快的速度是曼曼速度的倍,小快在由到骑行的途中与曼曼相遇于处,那么相遇时曼曼行走了多少米?(结果精确到米,) 24. 根据以下素材,探索完成任务.
24. 根据以下素材,探索完成任务.素材1
定义:如图1,点将线段分成两部分,如果 , 那么点称为线段的黄金分割点.
素材2
某兴趣小组在进行研究性学习时,由黄金分割点联想到“黄金分割线”,类似地给出黄金分割线的定义:直线将一个面积为的图形分成面积分别为 , 的两部分,如果 , 那么直线称为该图形的黄金分割线.
素材3
平行四边形是中心对称图形:在同一平面内,一个三角形绕其中一边的中点旋转 , 其余两边与旋转后相对应的两边组成一个平行四边形,例如,图2中的绕的中点旋转后与原三角形组成一个平行四边形(如图3).

问题解决
任务1
问题1:如图3,边上黄金分割点旋转后的对称点是否也是边上的黄金分割点?请写出你的判断结论,并说明理由.
问题2:直线是不是四边形的黄金分割线?请写出你的判断结论: .
任务2
请在图3探索:边上是否存在点 , 使得直线是四边形的黄金分割线?如果存在,请说明点的位置;如果不存在,请说明理由.
任务3
兴趣小组探索图2时猜想:在中,若点为边上的黄金分割点,连接 , 则直线是的黄金分割线,你认为对吗?为什么?
任务4
兴趣小组探索图2时还发现:若点是的边的黄金分割点,过点任意作一条直线交于点 , 再过点作交于点 , 则直线是的黄金分割线,请你给出证明.