四川省巴中市恩阳区2022-2023学年七年级下学期期中数学试卷

试卷更新日期：2023-06-06 类型：期中考试

进入出卷网下载

一、单选题

1. 下列方程是一元一次方程的是（）

A、 $x - 3 = y$ B、 $x^{2} - 1 = 0$ C、 $x - 2 = \frac{1}{3}$ D、 $\frac{2}{x} = 3$

查看试题解析
2. 将方程 $3 x + y = 9$ 写成用含y的式子表示x的形式，正确的是（）

A、 $y = 3 x - 9$ B、 $y = 9 - 3 x$ C、 $x = \frac{y}{3} - 3$ D、 $x = 3 - \frac{y}{3}$

查看试题解析
3. 关于x、y的二元一次方程组 ${\begin{array}{l} y = x + 3 \\ 2 x - y = 5 \end{array}$ ，用代入法消去y后所得到的方程，正确的是（）

A、 $2 x - x + 3 = 5$ B、 $2 x + x - 3 = 5$ C、 $2 x + x + 3 = 5$ D、 $2 x - x - 3 = 5$

查看试题解析
4. 交通法规人人遵守，文明城市处处安全.在通过桥洞时，我们往往会看到下图所示的标志，这是限制车高的标志，则通过该桥洞的车高 $x (m)$ 的范围可表示为（）

A、 $x \geq 4.5$ B、 $x > 4.5$ C、 $x \leq 4.5$ D、 $0 < x \leq 4.5$

查看试题解析
5. 已知“ $x > y$ ”，则下列不等式中，不成立的是（）

A、 $3 x > 3 y$ B、 $x - 9 > y - 9$ C、 $- x > - y$ D、 $- \frac{x}{2} < - \frac{y}{2}$

查看试题解析
6. 解方程 $\frac{x + 1}{3} - \frac{x - 1}{6} = 1$ 需下列四步，其中开始发生错误的一步是（）

A、去分母，得2（x+1）-（x-1）＝6 B、去括号，得2x+2-x+1＝6 C、移项，得2x-x＝6-2+1 D、合并同类项，得x＝5

查看试题解析
7. 已知关于 $x$ ， $y$ 的方程组 ${\begin{array}{l} x + 3 y = 4 - a \\ x - y = 3 a \end{array}$ ，给出下列结论：① ${\begin{array}{l} x = 5 \\ y = - 1 \end{array}$ 是方程组的一个解；②当 $a = 2$ 时，x，y的值互为相反数；③当 $a = 1$ 时，方程组的解也是方程 $x - 2 y = 3$ 的解；④x，y间的数量关系是 $x + y = 4 - a$ ，其中正确的是（）

A、②③ B、①②③ C、①③ D、①③④

查看试题解析
8. 《九章算术》是中国传统数学的重要著作，方程术是它的最高成就．其中记载：今有共买物，人出八，盈三；人出七，不足四，问人数、物价各几何？译文：今有人合伙购物，每人出8钱，会多3钱；每人出7钱，又会差4钱，问人数、物价各是多少？设合伙人数为 $x$ 人，物价为 $y$ 钱，以下列出的方程组正确的是（）

A、 ${\begin{array}{l} 8 x - y = 3 \\ y - 7 x = 4 \end{array}$ B、 ${\begin{array}{l} y - 8 x = 3 \\ 7 x - y = 0 \end{array}$ C、 ${\begin{array}{l} 8 x - y = 3 \\ 7 x - y = 4 \end{array}$ D、 ${\begin{array}{l} y - 8 x = 3 \\ y - 7 x = 4 \end{array}$

查看试题解析
9. 如图，在天平上放若干苹果和香蕉，其中①②的天平保持平衡，现要使③中的天平也保持平衡，需要在天平右盘中放入砝码（）

A、350克 B、300克 C、250克 D、200克

查看试题解析
10. 一个不等式组的解集在数轴上表示如图，则这个不等式组可能是（）

A、 ${\begin{array}{l} - 2 x < 6 \\ x \geq 2 \end{array}$ B、 ${\begin{array}{l} - 2 x > 6 \\ x \leq 2 \end{array}$ C、 ${\begin{array}{l} - 2 x > 6 \\ x \geq 2 \end{array}$ D、 ${\begin{array}{l} - 2 x < 6 \\ x \leq 2 \end{array}$

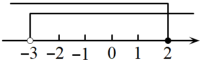查看试题解析
11. 幻方是古老的数学问题，我国古代的《洛书》中记载了最早的幻方——九宫格．将9个数填入幻方的空格中，要求每一横行、每一竖列以及两条对角线上的3个数之和相等，例如图（1）就是一个幻方．图（2）是一个末完成的幻方，则 $x - y$ 的值是（）

A、0 B、-4 C、-10 D、32

查看试题解析
12. 用若干个形状、大小完全相同的长方形纸片围成正方形，4个长方形纸片围成如图①所示的正方形，其阴影部分的面积为81，8个长方形纸片围成如图②所示的正方形，其阴影部分的面积为64，12个长方无纸片围成如图③所示的正方形，其阴影部分的面积为（）

A、48 B、36 C、50 D、49

查看试题解析

二、填空题

13. 当 $x =$ 时，代数式 $2 x - 1$ 的值与代数式 $3 x + 3$ 的值相等．

查看试题解析
14. 若 $m$ 与 $3$ 的和为非负数，则可列出不等式．

查看试题解析
15. 把一根长 $20 m$ 的钢管截成 $2 m$ 长和 $3 m$ 长两种规格均有的短钢管，且没有余料，不同的截法有种．

查看试题解析
16. 《孙子算经》是我国传统数学的重要著作之一，其中记载的“荡杯问题”很有趣．其内容为：2人同吃一碗饭，3人同吃一碗羹，4人同吃一碗肉，共用65个碗，问有客人．

查看试题解析
17. 在一家水果店，小明买了1斤苹果，4斤西瓜，2斤橙子，共付30元；小惠买了2斤苹果，6斤西瓜，2斤橙子，共付44元．则买1斤苹果和2斤西瓜一共需付元．

查看试题解析
18. 如图，已知正方形的边长为4，甲、乙两动点分别从正方形 $A B C D$ 的顶点A、C同时沿正方形的边开始移动，甲点依顺时针方向环行，乙点依逆时针方向环行，若乙的速度是甲的速度的3倍，则它们第2023次相遇在边．

查看试题解析

三、解答题

19. 解方程（组）．

(1)、 $5 x + 3 = 2 (x - 3)$

(2)、 ${\begin{array}{l} 3 y - 4 x = 0 \\ 4 x + y = 8 \end{array}$

(3)、 ${\begin{array}{l} 3 (x - 1) = y + 5 \\ \frac{y - 1}{3} = \frac{x}{5} + 1 \end{array}$

(4)、 ${\begin{array}{l} x + y = - 1 \\ x - y - z = 7 \\ 2 x - y - z = 0 \end{array}$

查看试题解析
20. 解不等式： $\frac{x - 4}{2} \leq 1 - \frac{7 - x}{3}$ ，将它的解集表示在数轴上并写出它的最大整数解．

查看试题解析
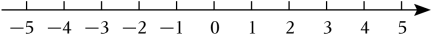21. 已知关于x，y的方程组 ${\begin{array}{l} 3 x - y = 5 \\ 4 a x + 5 b y = - 22 \end{array}$ 和 ${\begin{array}{l} 2 x + 3 y = - 4 \\ a x - b y = 8 \end{array}$ 有相同解，求 $（ - a ）^{b}$ 值．

查看试题解析
22. 规定 $| \begin{array}{l} a & c \\ b & d \end{array} | = a d - b c$ ，如 $| \begin{array}{l} 2 & - 1 \\ 3 & 0 \end{array} | = 2 \times 0 - 3 \times (- 1) = 3$ ．

(1)、 $| \begin{array}{l} - 2 & 3 \\ 5 & x + 1 \end{array} | = - 3$ ，求 $x$ 的值；

(2)、若 $| \begin{array}{l} 3 & - 2 \\ n & m \end{array} | = 1$ ， $| \begin{array}{l} 3 & 2 \\ m & n \end{array} | = - 5$ ，求 $m - n$ 的值．

查看试题解析
23. 如图，大长方形 $A B C D$ 中无重叠地放置9个形状、大小都相同的小长方形，已知大长方形的长与宽的差为2，小长方形的周长为14，求图中空白部分的面积．

查看试题解析
24. 为深入贯彻落实习近平总书记“绿水青山就是金山银山”的发展理念，某单位计划购买甲、乙两种树苗开展义务植树活动．若购买100棵甲树苗和200棵乙树苗需花费8000元，若购买甲树苗和乙树苗各150棵，则需花费7500元．

(1)、求甲、乙两种树苗每棵分别为多少元；

(2)、为提升绿化效果，单位决定购买甲、乙两种树苗共400棵，总费用不超过10000元，则最少购买多少棵甲树苗？

查看试题解析
25. 阅读理解：
在数学课上，李老师遇到下面问题：已知x，y满足方程组 ${\begin{array}{l} x + 3 y = - 1 \\ 3 x + y = 5 \end{array}$ ，求 $x + y$ 的值？
小红：把方程组解出来，再求 $x + y$ 的值．
小刚：把两个方程直接相加得 $4 x + 4 y = 4$ 方程两边同时除以 $4$ 解得 $x + y = 1$ ．
李老师对两位同学的讲解进行点评：指出“小刚”同学的思路体现了数学中【整体思想】的运用．
请你参考小红或小刚同学的做法，解决下面的问题．

(1)、已知关于 $x$ 、 $y$ 的方程组 ${\begin{array}{l} 2 x + y = 2 a + 1 \\ x + 2 y = 5 - 5 a \end{array}$ 的解满足 $x + y = - 3$ ，求 $a$ 的值．

(2)、运用【整体思想】解答：
若方程组 ${\begin{array}{l} a x + y = b \\ x - b y = a \end{array}$ 的解是 ${\begin{array}{l} x = 1 \\ y = 1 \end{array}$ ，求 ${(a ＋ b)}^{2} - (a - b) (a + b)$ 的值．

查看试题解析
26. 天虹超市销售东北大米，每包 $10 k g$ ，定价为100元．元旦期间进行促销活动，为满足大宗采购需求，超市制定了两种销售方案以供选择：
方案一：六折优惠并且免费送货上门；

方案二：买一送一，但需另付200元运费．

(1)、假设某食堂需要财买8包东北大米，且需送货上门．采用方案一购买，需要元；采用方案二购买，需要元．

(2)、假设某食堂需要购买 $x$ 包东北大米（ $x$ 是偶数），且需送货上门．
①采用方案一购买 $x$ 包东北大米需要 ▲ 元；采用方案二购买 $x$ 包东北大米需要 ▲ 元．

②某次进货时，食堂的采购员小王发现两种采购方案相差100元．请你算一算小王这次采购多少包东北大米？

查看试题解析