广东省深圳市蛇口育才教育集团育才三中2023年中考二模数学试题
试卷更新日期:2023-06-06 类型:中考模拟
一、选择题:(每小题只有一个正确选项,每小题3分,共计30分)
-
1. 的绝对值是( )A、 B、6 C、 D、2. 某几何体的表面展开图如图所示,那么这个几何体是( )
 A、圆锥 B、圆柱 C、三棱柱 D、三棱锥3. 据报道,2022年中国半导体投资中,芯片设计产业成为主力,投资规模超5600亿元.其中,5600亿用科学记数法表示为( )A、 B、 C、 D、4. 下列运算正确的是( )A、 B、 C、 D、5. 将一副三角板按如图所示的位置摆放在直尺上,则∠1的度数为( )
A、圆锥 B、圆柱 C、三棱柱 D、三棱锥3. 据报道,2022年中国半导体投资中,芯片设计产业成为主力,投资规模超5600亿元.其中,5600亿用科学记数法表示为( )A、 B、 C、 D、4. 下列运算正确的是( )A、 B、 C、 D、5. 将一副三角板按如图所示的位置摆放在直尺上,则∠1的度数为( ) A、45° B、65° C、75° D、85°6. 剪纸艺术是中国民间艺术之一,很多剪纸作品体现了数学中的对称美.如图,蝴蝶剪纸是一幅轴对称图形,将其放在平面直角坐标系中,如果图中点E的坐标为 , 其关于y轴对称的点F的坐标为 , 则的值为( )
A、45° B、65° C、75° D、85°6. 剪纸艺术是中国民间艺术之一,很多剪纸作品体现了数学中的对称美.如图,蝴蝶剪纸是一幅轴对称图形,将其放在平面直角坐标系中,如果图中点E的坐标为 , 其关于y轴对称的点F的坐标为 , 则的值为( ) A、 B、0 C、1 D、7. 《孙子算经》是中国传统数学的重要著作,其中有一道题,原文是:“今有木,不知长短,引绳度之,余绳四尺五寸;屈绳量之,不足一尺.木长几何?”意思是:用一根绳子去量一根木头的长,绳子还剩余4.5尺;将绳子对折再量木头,则木头还剩余1尺,问木头长多少尺?可设木头长为x尺,绳子长为y尺,则所列方程组正确的是( )A、 B、 C、 D、8. 下列说法正确的是( )A、五边形的外角和是540° B、对角线相等且互相垂直的四边形是正方形 C、因式分解是正确的 D、关于x的方程有两个不相等的实数根9. 如图,以正方形一边为斜边向外作直角三角形,再以该直角三角形的两直角边分别向外作正方形,重复这一过程就可以得到“勾股树”的部分图形.设大正方形N的边长为定值n , 小正方形B , C的边长分别为b , c . 已知 , 当角变化时,则b与c满足的关系式是( )
A、 B、0 C、1 D、7. 《孙子算经》是中国传统数学的重要著作,其中有一道题,原文是:“今有木,不知长短,引绳度之,余绳四尺五寸;屈绳量之,不足一尺.木长几何?”意思是:用一根绳子去量一根木头的长,绳子还剩余4.5尺;将绳子对折再量木头,则木头还剩余1尺,问木头长多少尺?可设木头长为x尺,绳子长为y尺,则所列方程组正确的是( )A、 B、 C、 D、8. 下列说法正确的是( )A、五边形的外角和是540° B、对角线相等且互相垂直的四边形是正方形 C、因式分解是正确的 D、关于x的方程有两个不相等的实数根9. 如图,以正方形一边为斜边向外作直角三角形,再以该直角三角形的两直角边分别向外作正方形,重复这一过程就可以得到“勾股树”的部分图形.设大正方形N的边长为定值n , 小正方形B , C的边长分别为b , c . 已知 , 当角变化时,则b与c满足的关系式是( ) A、 B、 C、 D、10. 如图,直线l:分别与x轴、y轴交于点A、B . 点P为直线l在第一象限的点.作△POB的外接圆 , 延长OC交于点D , 当△POD的面积最小时,则的半径长为( )
A、 B、 C、 D、10. 如图,直线l:分别与x轴、y轴交于点A、B . 点P为直线l在第一象限的点.作△POB的外接圆 , 延长OC交于点D , 当△POD的面积最小时,则的半径长为( )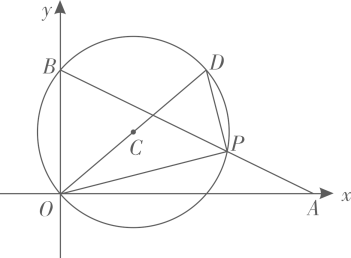 A、 B、2 C、 D、3
A、 B、2 C、 D、3二、填空题:(每小题3分,共计15分)
-
11. 若分式有意义,则x满足的条件是12. 学校招募校园广播员,从两名男生和两名女生共四名候选人中随机选取两人,则两人恰好是一男一女的概率13. 如图所示,热气球的探测器显示,从热气球A处看一栋楼顶部B处的仰角为30°,看这栋楼底部C处的俯角为60°,热气球A处与楼的水平距离为150米,则这栋楼的高度为米
 14. 如图,在平面直角坐标系中,菱形OABC的顶点A在x轴上,顶点C在反比例函数的图象上,且 . 若将该菱形向下平移2个单位后,顶点B恰好落在此反比例函数的图象上,则k的值为
14. 如图,在平面直角坐标系中,菱形OABC的顶点A在x轴上,顶点C在反比例函数的图象上,且 . 若将该菱形向下平移2个单位后,顶点B恰好落在此反比例函数的图象上,则k的值为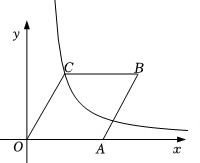 15. 如图,在Rt△ABC中, , , , 点M、N分别在AC、BC上,连接MN , 将△CMN沿MN翻折,使点C的对应点P落在AB的延长线上,若PM平分∠APN , 则MC长为
15. 如图,在Rt△ABC中, , , , 点M、N分别在AC、BC上,连接MN , 将△CMN沿MN翻折,使点C的对应点P落在AB的延长线上,若PM平分∠APN , 则MC长为
三、解答题:(本题共7小题,其中第16题5分,第17题7分,第18题8分,第19题8分,第20题8分,第21题9分,第22题10分,共55分)
-
16. 计算: .17. 先化简,再求值: , 其中 .18. 为了解双减背景下学生每天完成作业的时间情况,某中学对n名学生每天完成作业时间进行抽样调查,根据时间(单位:分钟)分成 , , , . 五个组,并将调查结果绘制成如图所示的两幅不完整的统计图.根据以上信息,回答下列问题:
 (1)、 , , 扇形统计图中A的圆心角度数为;(2)、补全条形统计图,学生每天完成作业时间的中位数落在组;(3)、若全校共有2000名学生,请估计该校每天完成作业时间不低于120分钟的学生有多少人?19. 端午节吃粽子是中华民族的传统习俗.某超市节前购进了甲、乙两种畅销口味的粽子.已知购进甲种粽子的金额是1200元,购进乙种粽子的金额是800元,购进甲种粽子的数量比乙种粽子的数量少50个,甲种粽子的单价是乙种粽子单价的2倍.(1)、求甲、乙两种粽子的单价分别是多少元?(2)、为满足消费者需求,该超市准备再次购进甲、乙两种粽子共200个,若总金额不超过1150元,问最多购进多少个甲种粽子?20. 如图,△ABC为的内接三角形,且AB为的直径,DE与相切于点D , 交AB的延长线于点E , 连接OD交BC于点F , 连接AD、CD , .
(1)、 , , 扇形统计图中A的圆心角度数为;(2)、补全条形统计图,学生每天完成作业时间的中位数落在组;(3)、若全校共有2000名学生,请估计该校每天完成作业时间不低于120分钟的学生有多少人?19. 端午节吃粽子是中华民族的传统习俗.某超市节前购进了甲、乙两种畅销口味的粽子.已知购进甲种粽子的金额是1200元,购进乙种粽子的金额是800元,购进甲种粽子的数量比乙种粽子的数量少50个,甲种粽子的单价是乙种粽子单价的2倍.(1)、求甲、乙两种粽子的单价分别是多少元?(2)、为满足消费者需求,该超市准备再次购进甲、乙两种粽子共200个,若总金额不超过1150元,问最多购进多少个甲种粽子?20. 如图,△ABC为的内接三角形,且AB为的直径,DE与相切于点D , 交AB的延长线于点E , 连接OD交BC于点F , 连接AD、CD , .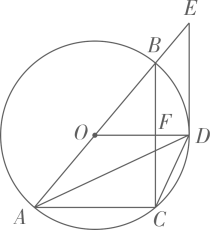 (1)、求证:AD平分∠BAC;(2)、若 , , 求的半径r .21. 【定义】在平面直角坐标系xOy中,对于点和点 , 给出如下定义:若 , 则称点Q为点P的限变点,例如:点的限变点的坐标是 , 点的限变点的坐标是 .
(1)、求证:AD平分∠BAC;(2)、若 , , 求的半径r .21. 【定义】在平面直角坐标系xOy中,对于点和点 , 给出如下定义:若 , 则称点Q为点P的限变点,例如:点的限变点的坐标是 , 点的限变点的坐标是 .【应用】
(1)、①点的限变点的坐标是;②以下三个选项中的点是反比例函数图象上某一个点的限变点的是()
A. B. C.
(2)、若点P在一次函数的图象上,请在下图平面直角坐标系中,画出点P的限变点Q的函数图象,并根据图象直接写出点Q的纵坐标的取值范围为 . (3)、【拓展】
(3)、【拓展】我国著名数学家华罗庚曾说过:“数形结合百般好,隔裂分家万事休”.若点P在关于x的二次函数的图象上,其限变点Q的纵坐标的取值范围是或 , 其中 , 令 , 求s关于t的函数解析式.
22. 已知正方形ABCD , 将边AB绕点A顺时针旋转至线段AE , ∠DAE的平分线所在直线与直线BE相交于点F .(1)、【探索发现】如图1,当为锐角时,请先用“尺规作图”作出∠DAE的平分线(保留作图痕迹,不写作法),再依题意补全图形,求证:;
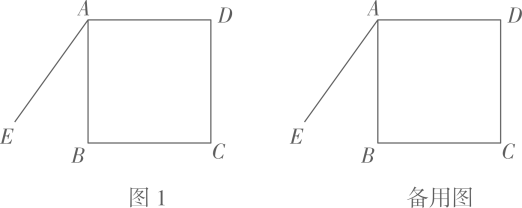 (2)、【深入探究】
(2)、【深入探究】在(1)的条件下 , ①∠DEB的度数为 ;②连接CF , 猜想线段BE和CF之间的数量关系,并证明;
(3)、【拓展思考】若正方形的边长 , 当以点C , F , D , E为顶点的四边形是平行四边形时,请直接写出线段BE的长度.