广东省茂名市高州市2022-2023学年七年级下学期5月月考数学试题

试卷更新日期：2023-06-06 类型：月考试卷

进入出卷网下载

一、选择题（本大题共10小题，每小题3分，共30分。在每小题给出的四个选项中，只有一项是正确的，请把正确答案代号填涂在答题卡相应位置上。）

1. 下面计算正确的是（）

A、 ${(a^{3})}^{4} = a^{12}$ B、 $a^{3} \cdot a^{5} = a^{15}$ C、 ${(x^{2} y)}^{3} = x^{6} y$ D、 $a^{6} \div a^{3} = a^{2}$

查看试题解析
2. 生物学家发现了一种病毒，其长度约为0.00000032mm，数据0.00000032用科学记数法表示正确的是（　　）

A、3.2×10⁷ B、3.2×10⁸ C、3.2×10^-7 D、3.2×10^-8

查看试题解析
3. 如图所示，下列判断错误的是（）

A、若∠1＝∠3，AD∥BC，则BD是∠ABC的平分线 B、若AD∥BC，则∠1＝∠2＝∠3 C、若∠3+∠4+∠C＝180°，则AD∥BC D、若∠2＝∠3，则AD∥BC

查看试题解析
4. 如图，A ， B ， C ， D在同一条直线上， $E C = B F$ ， $E C ∥ B F$ ，在下列条件中，不能使 $△ A E C$ 与 $△ D F B$ 全等的是（）

A、 $A E = D F$ B、 $A B = D C$ C、 $A E ∥ D F$ D、 $∠ E = ∠ F$

查看试题解析
5. 若a，b，c是△ABC的三边，则化简 $| a - b - c | - | b + a - c |$ 的结果是（）

A、 $2 b - 2 a$ B、 $2 c - 2 a$ C、 $2 b$ D、0

查看试题解析
6. 如图，描述了某汽车在行驶过程中速度与时间的关系图，下列说法中错误的是（）

A、第3分时汽车的速度是40千米/时 B、第12分时汽车的速度是0千米/时 C、从第3分到第6分，汽车行驶了120千米 D、从第9分到第12分，汽车的速度从60千米/时减少到0千米/时

查看试题解析
7. 下列说法：①在同一平面内，不相交的两条线段叫做平行线；②过直线外一点，有且只有一条直线平行于已知直线；③两条平行直线被第三条直线所截，同位角相等；④同旁内角相等，两直线平行．其中正确的个数有（）个．

A、4 B、3 C、2 D、1

查看试题解析
8. 下列各式：①(x-2y)(2y+x)； ② (x-2y)(-x-2y)； ③ (-x-2y)(x+2y)； ④(x-2y)(-x+2y).
其中能用平方差公式计算的是（）

A、①② B、②③ C、③④ D、①④

查看试题解析
9. 如图， $△ A B C$ 的面积为20，点D ， E ， F分别为 $B C ， A D ， C E$ 的中点，则阴影部分 $△ B F C$ 的面积为（）

A、4 B、5 C、6 D、10

查看试题解析
10. 如图，已知在 $△ A B C$ 中， $A B = A C$ ， $∠ B A C = 90 °$ ，直角 $∠ E P F$ 的顶点P是 $B C$ 的中点，两边 $P E$ 、 $P F$ 分别交 $A B$ 、 $A C$ 于点E、F.以下四个结论：① $A E = C F$ ；② $△ E P F$ 是等腰直角三角形；③ $S_{四边形 A E P F} = \frac{1}{2} S_{△ A B C}$ ；④ $E F = A P$ .其中正确的是（）

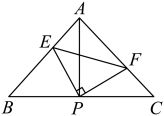A、①②③ B、①②④ C、②③④ D、①②③④

查看试题解析

二、填空题（本大题共5小题，每小题3分，共15分）

11. 已知 $x^{2} - k x + 16$ 是完全平方式，则 $k =$ .

查看试题解析
12. 如图，在△ABC中，∠C=90°，AD平分∠BAC，AB=5，CD=2，则△ABD的面积是．

查看试题解析
13. 若 $x^{2} + m x - 15 = (x + 3) (x + n)$ ，则m+n=；

查看试题解析
14. 一个三角形的两边长分别是2和7，最长边a为偶数，则这个三角形的周长为

查看试题解析
15. 如图，在 $△ A B C$ 中， $A B = 4$ ， $A C = 6$ ， $B C = 7$ ， $E F$ 垂直平分 $B C$ ，点 $D$ 为直线 $E F$ 上的一个动点，则 $△ A B D$ 周长的最小值是。

查看试题解析

三、解答题（一）（本大题共3小题，每小题8分，共24分）

16. 计算：

(1)、计算：－1²＋(－3)⁰－ ${(\begin{array}{l} - \frac{1}{3} \end{array})}^{- 2}$ ＋(－2)³

(2)、计算： $x （ 4 x - 1 ） - （ 2 x - 3 ）（ 2 x + 3 ） + （ x - 1 ）^{2}$ ；

查看试题解析
17. 已知：如图， $∠ 1 = ∠ C$ ， $∠ 2$ 和 $∠ D$ 互余， $B E ⊥ F D$ 于点 $G$ ，求证： $A B ∥ C D$ .

查看试题解析
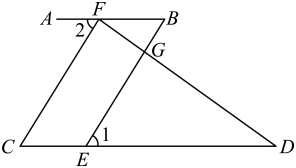18. 如图，在正方形网格上有一个 $△ A B C$ ．

(1)、画出 $△ A B C$ 关于直线 $M N$ 的对称图形 $△ DEF$ （不写画法）；

(2)、若网格上的每个小正方形的边长为1，求 $△ A B C$ 的面积．

查看试题解析

四、解答题（二）（本大题3小题，每小题9分，共27分）

19. 如图，在△ABC中，AB=AC，D、E是BC边上的点，连接AD，AE，以△ADE的边AE所在直线为对称轴作△ADE的轴对称图形△AD′E，连接D′C，若BD=CD′；

(1)、求证：△ABD≌△ACD′；

(2)、若∠BAC=120°，求∠DAE的度数。

查看试题解析
20. 小明用的练习本可以到甲超市购买，也可以到乙超市购买．已知两超市的标价都是每本1元，但甲超市的优惠条件是购买10本或少于10本按标价卖，10本以上，从第11本开始按标价的70%卖．乙超市的优惠条件是从第1本开始就按标价的85%卖．

(1)、当小明要买28本时，到哪家超市购买较省钱？

(2)、写出甲超市中，收款 $y_{甲}$ (元)与购买本数x(本)的关系式．

(3)、小明现有24元钱，最多可买多少本练习本？

查看试题解析
21. 如图，△ABC中，AB，AC的垂直平分线分别交BC于D，E两点，垂足分别是M，N.

(1)、若△ADE的周长是10，求BC的长；

(2)、若∠BAC＝100°，求∠DAE的度数．

查看试题解析

五、解答题（三）（本大题2小题，每小题12分，共24分）

22. 图1是一个长为2m、宽为2n的长方形，沿图中虚线用剪刀均分成四块小长方形，然后按图2的形状拼成一个正方形．

(1)、图2中的阴影部分的正方形的边长等于 ▲ ，观察图2你能写出下列三个代数式(m+n)² ， (m-n)² ， mn之间的等量关系 ▲ ，运用你所得到的公式，计算若mn=-2，m-n=4，求 (m+n)²的值。

(2)、已知 $x + \frac{1}{x} = 3$ ，求 ${(x - \frac{1}{x})}^{2}$ 值。

(3)、用完全平方公式和非负数的性质求解：已知a、b、c是 $△ A B C$ 的三边长，满足 $a^{2} + b^{2} = 10 a + 8 b - 41$ ，且c是 $△ A B C$ 最长的边，求c的取值范围。

查看试题解析
23. 如图（1）， $A B$ =16cm， $A C ⊥ A B$ ， $B D ⊥ A B$ ，垂足分别为A ， B ， AC=10cm．点P在线段 $A B$ 上以3cm/s的速度由点A向点B运动．同时，点Q在射线 $B D$ 上运动．它们运动的时间为t（s）（当点P运动结束时，点Q运动随之结束）．

(1)、若点Q的运动速度与点P的运动速度相等，当t=2时，
①试说明 $△ A C P ≌ △ B P Q$ ．

②此时，线段 $P C$ 和线段 $P Q$ 有怎样的关系，请说明理由．

(2)、如图（2），若“ $A C ⊥ A B$ ， $B D ⊥ A B$ ”改为“ $∠ C A B ＝ ∠ D B A ＝ 60 °$ ”，点Q的运动速度为xcm/s，其他条件不变，当点P ， Q运动到某处时，有 $△ A C P$ 和 $△ B P Q$ 全等，求出此时的x ， t的值。

查看试题解析