吉林省名校调研卷系列（省命题A）2022-2023学年七年级下学期期中数学试卷

试卷更新日期：2023-06-06 类型：期中考试

进入出卷网下载

一、单选题

1. 在平面直角坐标系中，下列各点在第二象限的是（）

A、 $(- 1 ， 2)$ B、 $(- 3 ， 0)$ C、 $(0 ， 4)$ D、 $(5 ， - 6)$

查看试题解析
2. 2的平方根是（）

A、 $\sqrt{2}$ B、 $\pm \sqrt{2}$ C、4 D、±4

查看试题解析
3. 在电影院放映厅中，若用（2，5）表示2排5号，则6排8号可以表示为（）

A、（2，8） B、（6，5） C、（6，8） D、（8，6）

查看试题解析
4. 在实数 $\sqrt{5}$ ，0， $\frac{π}{2}$ ， $\frac{3}{7}$ ， $\sqrt[3]{27}$ ，3.121121112…（每两个2之间依次多一个1）中无理数的个数有（）.

A、5个 B、4个 C、3个 D、2个

查看试题解析
5. 将一把直尺和一块含 $30 °$ 角的直角三角板按如图所示方式摆放，其中 $∠ C B D = 90 °$ ， $∠ B D C = 30 °$ ，若 $∠ 1 = 78 °$ ，则 $∠ 2$ 的度数为（）

A、 $12 °$ B、 $18 °$ C、 $42 °$ D、 $48 °$

查看试题解析
6. 如图．按下面的程序计算：若开始输入的x值为1．则最后输出的结果是（）

A、13 B、4 C、7 D、 $\sqrt{7}$

查看试题解析

二、填空题

7. 比较大小：－4 － $\sqrt{11}$ （填“>”或“<”）．

查看试题解析
8. 在平面直角坐标系中点 $A (6 ， - 2)$ 到y轴的距离是．

查看试题解析
9. 计算： $\sqrt{81} - \sqrt[3]{1000} =$ ．

查看试题解析
10. 如间是一只蝴蝶标本、将其放在适当的平面直角坐标系中，装翅膀网端点B、C的坐标分别为 $(- 1 ， 3) 、 (3 ， 0)$ ．则蝴蝶“尾部”点A的坐标为．

查看试题解析
11. 如图，请添加一个合适的条件，使 $A B ∥ C D$ ．

查看试题解析
12. 如果 $\sqrt[3]{4.8}$ $\approx$ 1.687， $\sqrt[3]{48} \approx$ 3.634，那么 $\sqrt[3]{4800} \approx$ ．

查看试题解析
13. 某宾馆在重新装修后，准备在大厅主楼梯上铺设某种红色地毯，已知这种地毯每平方米的售价为30元，主楼梯宽3米，其侧面如图所示，则购买地毯至少需要元．

查看试题解析
14. 若点 $A (a ， 1 - a)$ 在坐标轴上，则 $a =$ ．

查看试题解析

三、解答题

15. 求x的值： ${(x + 4)}^{3} - 64 = 0$ ．

查看试题解析
16. 计算： $| 1 - \sqrt{6} | - \sqrt{25} + \sqrt{{(- 3)}^{2}}$ ．

查看试题解析
17. 如图， $∠ A B C = 140 °$ ， $∠ 1 = 70 °$ ，将直线a平移后得到直线b，直线b经过点B，再将直线b平移得到直线c．求 $∠ 3$ 的度数．

查看试题解析
18. 已知一个正数m的两个平方根为 $3 a - 7$ 和 $a + 3$ ，求a和m的值．

查看试题解析
19. 如图，这是某校的平面示意图，如以正东为x轴正方向，正北为y轴正方向建立平面直角坐标系后，得到初中楼的坐标是 $(- 4 ， 2)$ ，实验楼的坐标是 $(- 4 ， 0)$ ．

(1)、坐标原点应为的位置．

(2)、在图中画出此平面直角坐标系；

(3)、校门在第象限；图书馆的坐标是；分布在第一象限的是．

查看试题解析
20. 如图，三角形 $A B C$ 在平面直角坐标系中的位置如图，解答下列问题．

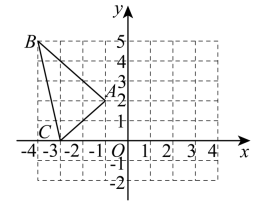(1)、写出点 $A B C$ 的坐标；

(2)、将三角形 $A B C$ 先向右平移5个单位长度，再向下平移2个单位长度，得到三角形 $A^{'} B^{'} C^{'}$ ，在平面直角坐标系中，画出三角形 $A^{'} B^{'} C^{'}$ ．

查看试题解析
21. 小悦想出一块面积为 $196 {cm}^{2}$ 的正方形纸片．沿着边的方向剪出一块面积为 $100 {cm}^{2}$ 的长方形纸片使它的长宽之比为 $2 ： 1$ ，小悦能用这块纸片裁出的符合要求的纸片吗?说明理由．

查看试题解析
22. 如图，直线EF交直线AB、CD与点M、N，NP平分∠ENC交直线AB于点P．
已知∠EMB=112°，∠PNC=34°．

(1)、求证：AB∥CD；

(2)、若PQ将分∠APN成两部分，且∠APQ：∠QPN=1：3，求∠PQD的度数．

查看试题解析
23. 已知 $2 a - 1$ 的平方根是 $\pm 3$ ， $3 a + b - 9$ 的立方根是2，c是 $\sqrt{7}$ 的整数部分.

(1)、求a，b，c的值；

(2)、求 $a + 2 b + c$ 的平方根.

查看试题解析
24. 在平面直角坐标系中，已知点 $M (m - 2 ， 2 m - 7)$ ，点 $N (n ， 3)$ ．

(1)、若M在x轴上，求M点的坐标；

(2)、若点M到x轴的距离等于3，求 $m$ 的值；

(3)、若 $M N ∥ y$ 轴，且 $M N = 2$ ，求 $n$ 的值．

查看试题解析
25. 如图， $∠ E D A =$ $α$ ， $∠ A B C =$ $β （ β$ $>$ $α$ ），解答下列问题．

(1)、如图①，当 $α$ $= 60 °$ ， $β$ $= 100 °$ 时，过点B在 $F D 、 B C$ 的内部作 $B F ∥ D E$ 则 $∠ F B C =$ 度；

(2)、如图②，点G在 $B C$ 上，过点G作 $M N ∥ D E$ ．
①当 $α$ $= 60 °$ ， $β$ $= 100 °$ 时，求 $∠ N G C$ 的度数；

②用含有 $α$ 和 $β$ 的式子表示 $∠ M G B$ ；

③当 $α$ $= 70 °$ ， $β$ $= 100 °$ 时，过点G作 $G H ⊥ B C$ ，直接写出 $∠ H G M$ 的度数．

查看试题解析
26. 如图，在以点O为原点的平面直角坐标系中，点A、B的坐标分别为 $(a ， 0) 、 (a ， b)$ ，点C在y轴上，且 $B C ∥ x$ 轴，a、b满足 $| a － 3 | ＋$ $\sqrt{b - 4}$ $= 0$ ，一动点P从原点出发，以每秒一动点P从原点出发，以每秒2个单位长度的速度沿着O－A－B－C－O的路线运动（回到点O时停止）

(1)、直接写出点A、B、C的坐标；

(2)、在点P运动的过程中，连接 $P O$ ，若 $P O$ 把四边形 $A B C O$ 的面积分成 $1 ： 2$ 两部分，求点P的坐标；

(3)、点P运动t秒后 $(t \neq 0)$ ，是否存在点P到x轴的距离为 $\frac{1}{2}$ $t$ 个单位长度的情况．若存在，求点P的坐标；若不存在，请说明理由．

查看试题解析