浙江省温州市2023年中考二模数学试题
试卷更新日期:2023-06-06 类型:中考模拟
一、单选题
-
1. 在4,-2,0,四个数中,最小的为( )A、4 B、-2 C、0 D、2. 2023年2月10日,神舟十五号航天员乘组圆满完成了首次出舱任务,据了解,这艘飞船的时速为每小时28000千米,28000千米用科学记数法表示应为( )A、千米 B、千米 C、千米 D、千米3. 下列各图形中,经过折叠能围成一个立方体的为( )A、
 B、
B、 C、
C、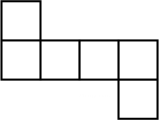 D、
D、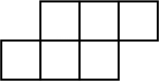 4. 不等式的解集在数轴上表示正确的为( )A、
4. 不等式的解集在数轴上表示正确的为( )A、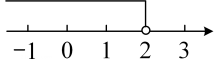 B、
B、 C、
C、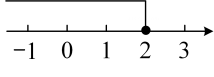 D、
D、 5. 一次对若干名青少年进行最喜爱的运动项目的问卷调查,得到如图的统计图.若最喜爱足球的人数比最喜爱游泳的人数多人,则这次问卷调查的总人数为( )
5. 一次对若干名青少年进行最喜爱的运动项目的问卷调查,得到如图的统计图.若最喜爱足球的人数比最喜爱游泳的人数多人,则这次问卷调查的总人数为( ) A、人 B、人 C、人 D、人6. 化简的结果为( )A、a B、 C、 D、7. 如图, , 为的两条弦,连结 , , 点为的延长线上一点.若 , 则为( )
A、人 B、人 C、人 D、人6. 化简的结果为( )A、a B、 C、 D、7. 如图, , 为的两条弦,连结 , , 点为的延长线上一点.若 , 则为( )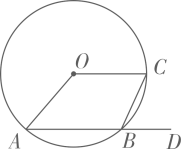 A、 B、 C、 D、8. 中国清代算书《御制数理精蕴》中有这样一题:“马四匹、牛六头,共价四十八两(‘两’为我国古代货币单位);马二匹、牛五头,共价三十八两,阀马、牛各价几何?”设马每匹x两,牛每头y两,根据题意可列方程组为( )A、 B、 C、 D、9. 将二次函数的图象向左平移m个单位后过点 , 则m的值为( )A、2 B、3 C、4 D、510. 如图是由四个全等的直角三角形和一个小正方形组成,恰好拼成一个大正方形 , 小正方形的对角线向两边延长,分别交边于点 , 交边于点 . 若是的中点,则的值为( )
A、 B、 C、 D、8. 中国清代算书《御制数理精蕴》中有这样一题:“马四匹、牛六头,共价四十八两(‘两’为我国古代货币单位);马二匹、牛五头,共价三十八两,阀马、牛各价几何?”设马每匹x两,牛每头y两,根据题意可列方程组为( )A、 B、 C、 D、9. 将二次函数的图象向左平移m个单位后过点 , 则m的值为( )A、2 B、3 C、4 D、510. 如图是由四个全等的直角三角形和一个小正方形组成,恰好拼成一个大正方形 , 小正方形的对角线向两边延长,分别交边于点 , 交边于点 . 若是的中点,则的值为( )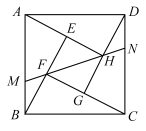 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. 分解因式:2x2﹣8=12. 一只不透明的袋子里装有9个只有颜色不同的球,其中有3个黑球,4个白球和2个红球,搅匀后随机摸出一个球,是白球的概率为 .13. 如图,圆锥形纸帽的高为 , 底面半径为 , 则这个纸帽的侧面积为 .
 14. 如图,菱形花坛的边长为米, , 其中由两个正六边形组成的部分种花,则种花部分的面积为 .
14. 如图,菱形花坛的边长为米, , 其中由两个正六边形组成的部分种花,则种花部分的面积为 . 15. 如图,点A在x轴上,以为边作矩形 , 反比例函数的图象经过的中点E,交边于点D,连结 . 若 , , 则k的值为 .
15. 如图,点A在x轴上,以为边作矩形 , 反比例函数的图象经过的中点E,交边于点D,连结 . 若 , , 则k的值为 .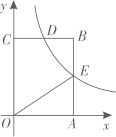 16. 如图1是一款便携式拉杆车,其侧面示意图如图2所示,前轮的直径为 , 拖盘与后轮相切于点N,手柄 . 侧面为矩形ABCD的货物置于拖盘上, , . 如图3所示,倾斜一定角度拉车时,货物绕点B旋转,点C落在上,若 , 则的长为 , 同一时刻,点C离地面高度 , 则点A离地面高度为 .
16. 如图1是一款便携式拉杆车,其侧面示意图如图2所示,前轮的直径为 , 拖盘与后轮相切于点N,手柄 . 侧面为矩形ABCD的货物置于拖盘上, , . 如图3所示,倾斜一定角度拉车时,货物绕点B旋转,点C落在上,若 , 则的长为 , 同一时刻,点C离地面高度 , 则点A离地面高度为 .

三、解答题
-
17.(1)、计算: .(2)、解方程: .18. 如图,在和中, , , , 连接BD,CE.
 (1)、求证: .(2)、若 , 求的度数.19. 质量检测部门对甲、乙两家公司销售的某电子产品的使用寿命进行跟踪调查,均取10件,统计结果如下(单位:年):
(1)、求证: .(2)、若 , 求的度数.19. 质量检测部门对甲、乙两家公司销售的某电子产品的使用寿命进行跟踪调查,均取10件,统计结果如下(单位:年): (1)、分别求出这两组数据的平均数.(2)、如果你是甲公司的推销员,请你结合相关统计量及折线统计图,对本公司的产品进行推销.20. 如图在的方格纸中,线段的端点均在格点上,请按要求在四边形的边上画格点M,N.
(1)、分别求出这两组数据的平均数.(2)、如果你是甲公司的推销员,请你结合相关统计量及折线统计图,对本公司的产品进行推销.20. 如图在的方格纸中,线段的端点均在格点上,请按要求在四边形的边上画格点M,N. (1)、在图1中作线段 , 使得平分 .(2)、在图2中作四边形 , 且 .21. 如图,在中,于点D,E,F分别为 , 的中点,G为边上一点, , 连结 .
(1)、在图1中作线段 , 使得平分 .(2)、在图2中作四边形 , 且 .21. 如图,在中,于点D,E,F分别为 , 的中点,G为边上一点, , 连结 .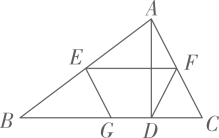 (1)、求证:四边形是平行四边形.(2)、若 , , , 求的长.22. 已知点 , , 在二次函数的图象上,且 .(1)、求该二次函数的表达式.(2)、已知点在对称轴的异侧,当时,二次函数的最大值与最小值的差为5,设 , 的最小值分别为 , 求的值.23. 根据以下素材,探索完成任务.
(1)、求证:四边形是平行四边形.(2)、若 , , , 求的长.22. 已知点 , , 在二次函数的图象上,且 .(1)、求该二次函数的表达式.(2)、已知点在对称轴的异侧,当时,二次函数的最大值与最小值的差为5,设 , 的最小值分别为 , 求的值.23. 根据以下素材,探索完成任务.探究遮阳伞下的影子长度
素材1
图1是某款自动旋转遮阳伞,伞面完全张开时张角呈 , 图2是其侧面示意图.已知支架AB长为2.5米,且垂直于地面BC,悬托架米,点E固定在伞面上,且伞面直径DF是DE的4倍.当伞面完全张开时,点D,E,F始终共线.为实现遮阳效果最佳,伞面装有接收器可以根据太阳光线的角度变化,自动调整手柄D沿着AB移动,以保证太阳光线与DF始终垂直.

素材2
时刻
12点
13点
14点
15点
16点
17点
太阳高度(度)
90
75
60
45
30
15
参考数据: , .
某地区某天下午不同时间的太阳高度角(太阳光线与地面的夹角)参照表:
素材3
小明坐在露营椅上的高度(头顶到地面的距离)约为1米.如图2,小明坐的位置记为点Q.
问题解决
任务1
确定影子长度
某一时刻测得米,请求出此时影子的长度.
任务2
判断是否照射到
这天14点,小明坐在离支架3米处的Q点,请判断此时小明是否会被太阳光照射到?
任务3
探究合理范围
小明打算在这天14:00-15:00露营休息,为保证小明全程不被太阳光照射到,请计算的取值范围.
24. 如图,在圆内接四边形中, , 的延长线交于点 , 连结并延长交于点 , 连结 . 已知 , , , . (1)、求证: .(2)、求与的长.(3)、是中点,动点在上从点向终点匀速运动,同时动点在上从点向终点匀速运动.当点在点处时,点在点处,设 , .
(1)、求证: .(2)、求与的长.(3)、是中点,动点在上从点向终点匀速运动,同时动点在上从点向终点匀速运动.当点在点处时,点在点处,设 , .①求关于的表达式.
②连结 , 当直线与的某一边所在的直线垂直时,记垂足为点 , 求的值.