浙江省宁波市慈溪市部分校2023年联考中考数学二模试题
试卷更新日期:2023-06-06 类型:中考模拟
一、单选题
-
1. 2023的相反数是( )A、2023 B、 C、 D、-20232. 下列运算中,正确的是( )A、5a+2b=7ab B、2a3+3a2=5a5 C、3a2b-3ba2=0 D、5a2-4a2=13. 从嫦娥一号升空,到嫦娥五号携月壤返回,中国人一步步将“上九天揽月”的神话变为现实.已知地球和月球间的平均距离约为 , 384000用科学记数法表示为( )A、 B、 C、 D、4. 如图所示几何体的主视图是( )
 A、
A、 B、
B、 C、
C、 D、
D、 5. 一个不透明的袋子里装有5个小球,它们除分别标有的数字1,2,3,4,5不同外,其他完全相同,任意从袋子中摸出一球,则摸出的球所标数字为奇数的概率是( )A、 B、 C、 D、6. 圆锥的母线长为4,底面半径为2,则此圆锥的侧面积是( )A、 B、 C、 D、7. 某青年排球队12名队员的年龄情况如表:
5. 一个不透明的袋子里装有5个小球,它们除分别标有的数字1,2,3,4,5不同外,其他完全相同,任意从袋子中摸出一球,则摸出的球所标数字为奇数的概率是( )A、 B、 C、 D、6. 圆锥的母线长为4,底面半径为2,则此圆锥的侧面积是( )A、 B、 C、 D、7. 某青年排球队12名队员的年龄情况如表:年龄(单位:岁)
18
19
20
21
22
人数
1
4
3
2
2
则这12名队员的年龄( )
A、众数是19,中位数是19 B、众数是19,中位数是19.5 C、众数是19,中位数是20 D、众数是19,中位数是20.58. 如图,ΔABC中,∠C=90°,AC=BC,AD平分∠CAB,交BC于D,DE⊥AB于E,且AB=6cm, 则ΔDEB的周长为( )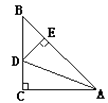 A、4cm B、6cm C、10cm D、以上都不对9. 已知抛物线y=ax2+bx+c(a,b,c是常数,且a≠0)与x轴相交于点A,B(点A在点B左侧),点A(-1,0),与y轴交于点C(0,c),其中2≤c≤3.对称轴为直线x=1,现有如下结论:①2a+b=0;②当x≥3时,y<0;③这个二次函数的最大值的最小值为;④-1≤a≤-其中正确结论的个数有( )个A、4 B、3 C、2 D、110. 如图,在矩形ABCD中,AD=AB,∠BAD的平分线交BC于点E,DH⊥AE于点H,连接DE,下列结论:①∠AED=∠CED;②△AED为等腰三角形;③EH=CE;④图中有3个等腰三角形.结论正确的个数为( )
A、4cm B、6cm C、10cm D、以上都不对9. 已知抛物线y=ax2+bx+c(a,b,c是常数,且a≠0)与x轴相交于点A,B(点A在点B左侧),点A(-1,0),与y轴交于点C(0,c),其中2≤c≤3.对称轴为直线x=1,现有如下结论:①2a+b=0;②当x≥3时,y<0;③这个二次函数的最大值的最小值为;④-1≤a≤-其中正确结论的个数有( )个A、4 B、3 C、2 D、110. 如图,在矩形ABCD中,AD=AB,∠BAD的平分线交BC于点E,DH⊥AE于点H,连接DE,下列结论:①∠AED=∠CED;②△AED为等腰三角形;③EH=CE;④图中有3个等腰三角形.结论正确的个数为( )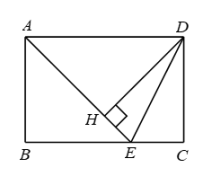 A、1个 B、2个 C、3个 D、4个
A、1个 B、2个 C、3个 D、4个二、填空题
-
11. 请任意写出一个介于到之间的数.12. 因式分解: .13. 如果方程的解是正数,那么的取值范围为 .14. 在我国古代数学著作《九章算术》中记载了一道有趣的数学问题:
“今有凫起南海,七日至北海;雁起北海,九日至南海.今凫雁俱起,问何日相逢?”意思是:野鸭从南海起飞,7天飞到北海;大雁从北海起飞,9天飞到南海.野鸭与大雁从南海和北海同时起飞,经过几天相遇.设野鸭与大雁从南海和北海同时起飞,经过x天相遇,根据题意,列方程 .
 15. 如图,在平面直角坐标系xOy中,点B在x轴正半轴上,点D在y轴正半轴上,⊙C经过A,B,D,O四点,∠OAB=120°,OB=4 , 则点D的坐标是 .
15. 如图,在平面直角坐标系xOy中,点B在x轴正半轴上,点D在y轴正半轴上,⊙C经过A,B,D,O四点,∠OAB=120°,OB=4 , 则点D的坐标是 . 16. 如图,平行四边形中,对角线交于点 , 双曲线经过两点,平行四边形的面积为24,则的面积为 , k=
16. 如图,平行四边形中,对角线交于点 , 双曲线经过两点,平行四边形的面积为24,则的面积为 , k=
三、解答题
-
17. 计算:(1)、(2)、.18. 如图,每个小正方形的边长都是的方格纸中,有线段和线段 , 点、、、的端点都在小正方形的顶点上.
 (1)、在方格纸中画出一个以线段为一边的菱形 , 所画的菱形的各顶点必须在小正方形的顶点上,并且其面积为20.(2)、在方格纸中以为底边画出等腰三角形 , 点在小正方形的顶点上,且的面积为5.连接 , 并直接写出的长.19. 如图,在平面直角坐标系中,抛物线经过点 , 顶点为A,连结 .
(1)、在方格纸中画出一个以线段为一边的菱形 , 所画的菱形的各顶点必须在小正方形的顶点上,并且其面积为20.(2)、在方格纸中以为底边画出等腰三角形 , 点在小正方形的顶点上,且的面积为5.连接 , 并直接写出的长.19. 如图,在平面直角坐标系中,抛物线经过点 , 顶点为A,连结 .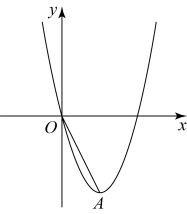 (1)、求a的值.(2)、求A的坐标.(3)、P为x轴上的动点,当时,请直接写出OP的长.20. 首届全民阅读大会于2022年4月23日在北京开幕,大会主题是“阅读新时代·奋进新征程”.按国务院教育督导委员会办公室印发的《关于组织责任督学进行“五项管理”督导的通知》要求,各中小学校积极行动,取得了良好的成绩.某中学随机抽取了部分学生,对他们一周的课外阅读时间(A:以上,B: , C: , D:以下)进行问卷调查,将所得数据进行分类,统计绘制了如下不完整的统计图.请根据图中的信息解答下列问题:
(1)、求a的值.(2)、求A的坐标.(3)、P为x轴上的动点,当时,请直接写出OP的长.20. 首届全民阅读大会于2022年4月23日在北京开幕,大会主题是“阅读新时代·奋进新征程”.按国务院教育督导委员会办公室印发的《关于组织责任督学进行“五项管理”督导的通知》要求,各中小学校积极行动,取得了良好的成绩.某中学随机抽取了部分学生,对他们一周的课外阅读时间(A:以上,B: , C: , D:以下)进行问卷调查,将所得数据进行分类,统计绘制了如下不完整的统计图.请根据图中的信息解答下列问题:
 (1)、求本次调查的学生人数;(2)、求出a,b的值并补全条形统计图;(3)、若该校有3600名学生,请估计该校一周课外阅读时间以上的人数.21. 如图1,平面直角坐标系中, , 反比例函数的图象分别交矩形的两边、于E、F(E、F不与A重合),沿着将矩形折叠使A、D重合.
(1)、求本次调查的学生人数;(2)、求出a,b的值并补全条形统计图;(3)、若该校有3600名学生,请估计该校一周课外阅读时间以上的人数.21. 如图1,平面直角坐标系中, , 反比例函数的图象分别交矩形的两边、于E、F(E、F不与A重合),沿着将矩形折叠使A、D重合.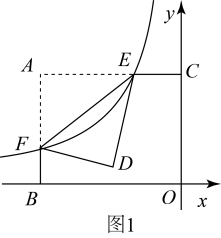
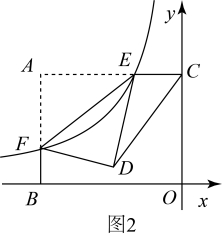
 (1)、当点E为中点时,求点F的坐标,并直接写出与对角线的关系;(2)、如图2,连接 .
(1)、当点E为中点时,求点F的坐标,并直接写出与对角线的关系;(2)、如图2,连接 .①的周长是否有最小值,若有,请求出最小值;若没有,请说明理由;
②当平分时,直接写出k的值.
22. 四边形ABCD和四边形AMPN有公共顶点A,连接BM和DN. (1)、如图1,若四边形ABCD和四边形AMPN都是正方形,当正方形AMPN绕点A旋转角()时,BM和DN的数量关系是 , 位置关系是;(2)、如图2,若四边形ABCD和四边形AMPN都是矩形,且 , 判断BM和DN的数量关系和位置关系,并说明理由;(3)、在(2)的条件下,若 , 矩形AMPN绕点A逆时针旋转角(),当时,求线段DN的长.23. 图形变换中的数学,问题情境:在课堂上,兴趣学习小组对一道数学问题进行了深入探究,在Rt△ABC中,∠ACB=90°,∠A=30°,点D是AB的中点,连接CD.
(1)、如图1,若四边形ABCD和四边形AMPN都是正方形,当正方形AMPN绕点A旋转角()时,BM和DN的数量关系是 , 位置关系是;(2)、如图2,若四边形ABCD和四边形AMPN都是矩形,且 , 判断BM和DN的数量关系和位置关系,并说明理由;(3)、在(2)的条件下,若 , 矩形AMPN绕点A逆时针旋转角(),当时,求线段DN的长.23. 图形变换中的数学,问题情境:在课堂上,兴趣学习小组对一道数学问题进行了深入探究,在Rt△ABC中,∠ACB=90°,∠A=30°,点D是AB的中点,连接CD.
探索发现:
(1)、如图①,BC与BD的数量关系是;(2)、如图①,CD与AB的数量关系是 ▲ ;并说明理由.(3)、如图②,若P是线段CB上一动点(点P不与点B,C重合),连接DP,将线段DP绕点D逆时针旋转60°,得到线段DF,连接BF,请猜想BF,BP,BD三者之间的数量关系,并证明你的结论;(4)、若点P是线段CB延长线上一动点,按照(3)中的作法,请在图③中补全图象,并直接写出BF、BP、BD三者之间的数量关系.24. 已知二次函数的图象经过点.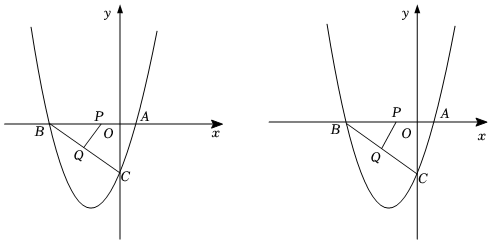 (1)、求该二次函数的表达式;(2)、二次函数图象与轴的另一个交点为 , 与轴的交点为 , 点从点出发在线段上以每秒2个单位长度的速度向点运动,同时点从点出发,在线段上以每秒1个单位长度的速度向点运动,直到其中一点到达终点时,两点停止运动,求面积的最大值;(3)、在点、运动的过程中,是否存在使与相似的时刻,如果存在,求出运动时间 , 如果不存在,请说明理由.
(1)、求该二次函数的表达式;(2)、二次函数图象与轴的另一个交点为 , 与轴的交点为 , 点从点出发在线段上以每秒2个单位长度的速度向点运动,同时点从点出发,在线段上以每秒1个单位长度的速度向点运动,直到其中一点到达终点时,两点停止运动,求面积的最大值;(3)、在点、运动的过程中,是否存在使与相似的时刻,如果存在,求出运动时间 , 如果不存在,请说明理由.