浙江省宁波市2023年中考三模数学试题
试卷更新日期:2023-06-06 类型:中考模拟
一、单选题
-
1. 计算 , 结果正确的是( )A、-5 B、1 C、5 D、-12. 下列计算正确的是( )A、 B、 C、 D、3. 2022年2月4日,北京第二十四届冬季奥林匹克运动会开幕式在国家体育场隆重举行,中国大陆地区观看人数约316000000人.用科学记数法表示316000000是( )A、3.16×107 B、31.6×107 C、3.16×108 D、0.316×1094. 如图,该几何体的主视图是( )
 A、
A、 B、
B、 C、
C、 D、
D、 5. 小玲在一次班会中参与知识抢答活动,现有语文题6个,数学题5个,英语题9个,她从中随机抽取1个,抽中数学题的概率是( )
5. 小玲在一次班会中参与知识抢答活动,现有语文题6个,数学题5个,英语题9个,她从中随机抽取1个,抽中数学题的概率是( )
A、 B、 C、 D、6. 若分式有意义,则x的取值应满足( )A、 B、 C、 D、7. 如图,在△ABC中,∠C=90°,AC=3,点P为△ABC外一点,连接AP、BP,点M、N分别为AP、BP的中点,若MN=2,则BC的长为( ) A、2 B、 C、 D、58. 中国古代人民很早就在生产生活中发现了许多有趣的数学问题,其中《孙子算经》中有个问题:今有三人共车,二车空;二人共车,九人步,问人与车各几何?这道题的意思是:今有若干人乘车,每三人共乘一车,最终剩余2辆车;若每2人共乘一车,最终剩余9个人无车可乘.问有多少人,多少辆车?设共有x人,y辆车,可列方程组为( )A、 B、 C、 D、9. 二次函数y=ax2+bx+c(a≠0)的图象如图所示,则下列结论不正确的是( )
A、2 B、 C、 D、58. 中国古代人民很早就在生产生活中发现了许多有趣的数学问题,其中《孙子算经》中有个问题:今有三人共车,二车空;二人共车,九人步,问人与车各几何?这道题的意思是:今有若干人乘车,每三人共乘一车,最终剩余2辆车;若每2人共乘一车,最终剩余9个人无车可乘.问有多少人,多少辆车?设共有x人,y辆车,可列方程组为( )A、 B、 C、 D、9. 二次函数y=ax2+bx+c(a≠0)的图象如图所示,则下列结论不正确的是( ) A、abc<0 B、a+b>m(am+b)(m≠1) C、4a-2b+c<0 D、3a+c=110. 如图,正六边形 , P点在上,记图中的面积为 , 已知正六边形边长,下列式子中不能确定的式子的是( )
A、abc<0 B、a+b>m(am+b)(m≠1) C、4a-2b+c<0 D、3a+c=110. 如图,正六边形 , P点在上,记图中的面积为 , 已知正六边形边长,下列式子中不能确定的式子的是( )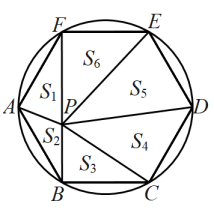 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. -64的立方根是 。12. 分解因式: .13. 某射击队从甲、乙、丙、丁四人中选拔一人参加射击比赛,在队内选拔赛中,每人射击10次,四人成绩的平均数(单位:环)及方差(单位:环2)如表所示:
甲
乙
丙
丁
平均数
8.5
8.2
8.5
8.2
方差
1.7
2.3
2
1.8
根据表中数据选择其中一人参加比赛,最合适的人选是 .
14. 如图是一个由三条等弧围成的莱洛三角形,其中 的圆心为点 , .若 ,则该三角形的周长是 . 15. 对于平面直角坐标系中的任意一点 , 我们把点称为点P的“和差点”.如图,的直角边在x轴上,点 , 若点P在反比例函数的图象上,点Q为点P的“和差点”,且点Q在的直角边上,则的面积为 .
15. 对于平面直角坐标系中的任意一点 , 我们把点称为点P的“和差点”.如图,的直角边在x轴上,点 , 若点P在反比例函数的图象上,点Q为点P的“和差点”,且点Q在的直角边上,则的面积为 . 16. 如图,在矩形中, . 将矩形沿折叠,使点A落在边上的E处,得到四边形 , 连接 , 若 , , 则 , .
16. 如图,在矩形中, . 将矩形沿折叠,使点A落在边上的E处,得到四边形 , 连接 , 若 , , 则 , .
三、解答题
-
17. 计算:(1)、(2)、解不等式组 .18. 如图,在68的网格图中,A,B,C三点都在格点上,按照如下要求找格点,

 (1)、在图1中画出四边形ABCD为中心对称图形;(2)、在图2中画出四边形ABCE为轴对称图形.19. 如图,葡萄园大棚支架的顶部形如等腰△ABC.经测量,钢条AD⊥BC,BC=600cm,∠B=38°.(精确到1cm,参考数据:sin 38°≈0.616,cos 38°≈0.788,tan 38°≈0.781)
(1)、在图1中画出四边形ABCD为中心对称图形;(2)、在图2中画出四边形ABCE为轴对称图形.19. 如图,葡萄园大棚支架的顶部形如等腰△ABC.经测量,钢条AD⊥BC,BC=600cm,∠B=38°.(精确到1cm,参考数据:sin 38°≈0.616,cos 38°≈0.788,tan 38°≈0.781) (1)、求钢条AB的长.(2)、为了加固支架,现在顶部加两根钢条DE和DF,已知DE⊥AB于点E,DF⊥AC于点F,求DE的长.20. 垃圾的分类处理与回收利用,可以减少污染,节省资源.某城市环保部门抽样调查了某居民小区一段时间内生活垃圾的分类情况,将获得的数据整理绘制成如图两幅不完整的统计图.(注:A为厨余垃圾,B为可回收垃圾,C为其它垃圾,D为有害垃圾)
(1)、求钢条AB的长.(2)、为了加固支架,现在顶部加两根钢条DE和DF,已知DE⊥AB于点E,DF⊥AC于点F,求DE的长.20. 垃圾的分类处理与回收利用,可以减少污染,节省资源.某城市环保部门抽样调查了某居民小区一段时间内生活垃圾的分类情况,将获得的数据整理绘制成如图两幅不完整的统计图.(注:A为厨余垃圾,B为可回收垃圾,C为其它垃圾,D为有害垃圾)
根据统计图提供的信息,解答下列问题:
(1)、在这次抽样调查中,一共有 ▲ 吨的生活垃圾;并补全条形统计图;(2)、扇形统计图中,B所对应的百分比是 , D所对应的圆心角度数是;(3)、假设该城市每月产生的生活垃圾为400吨,且全部分类处理,请估计每月产生的有害垃圾有多少吨?21. 如图,已知二次函数的图象经过点 . (1)、求该二次函数的表达式.(2)、求该二次函数图象的顶点坐标.(3)、点在该二次函数的图象上,若 , 试根据图象直接写出m的取值范围.22. “戴口罩、勤洗手、常通风”已成为当下人们的生活习惯,某校为做好校园防护工作.计划采购一批洗手液,已知某超市推出以下两种优惠方案:
(1)、求该二次函数的表达式.(2)、求该二次函数图象的顶点坐标.(3)、点在该二次函数的图象上,若 , 试根据图象直接写出m的取值范围.22. “戴口罩、勤洗手、常通风”已成为当下人们的生活习惯,某校为做好校园防护工作.计划采购一批洗手液,已知某超市推出以下两种优惠方案:方案一:一律打八折.
方案二:购买量不超过200瓶时,按原价销售;超过200瓶时,超过的部分打六折.
设学校计划从该超市购买x瓶洗手液,方案一的费用为元,方案二的费用为元.关于x的函数图象如图所示.
 (1)、该洗手液的标价为元/瓶;(2)、若 , 求关于x的函数解析式;(3)、若该校计划购买420瓶洗手液.则选择哪种方案更省钱?请说明理由.23. 如图
(1)、该洗手液的标价为元/瓶;(2)、若 , 求关于x的函数解析式;(3)、若该校计划购买420瓶洗手液.则选择哪种方案更省钱?请说明理由.23. 如图 (1)、【问题发现】如图1,P是半径为2的⊙O上一点,直线m是⊙O外一直线,圆心O到直线m的距离为3,PQ⊥m于点Q,则PQ的最大值为;(2)、【问题探究】如图2,将两个含有30°角的直角三角板的60°角的顶点重合(其中∠A==30°,∠C=∠C'=90°),绕点B旋转 , 当旋转至CC′=4时,求的长;(3)、【问题解决】如图3,点O为等腰RtABC的斜边AB的中点,AC=BC=5 , OE=2,连接BE,作RtBEF,其中∠BEF=90°,tan∠EBF= , 连接AF,求四边形ACBF的面积的最大值.24. 如图,内接于圆O, , 点D为劣弧上动点,延长 , 交于点E,作交圆O于点F,连接 .
(1)、【问题发现】如图1,P是半径为2的⊙O上一点,直线m是⊙O外一直线,圆心O到直线m的距离为3,PQ⊥m于点Q,则PQ的最大值为;(2)、【问题探究】如图2,将两个含有30°角的直角三角板的60°角的顶点重合(其中∠A==30°,∠C=∠C'=90°),绕点B旋转 , 当旋转至CC′=4时,求的长;(3)、【问题解决】如图3,点O为等腰RtABC的斜边AB的中点,AC=BC=5 , OE=2,连接BE,作RtBEF,其中∠BEF=90°,tan∠EBF= , 连接AF,求四边形ACBF的面积的最大值.24. 如图,内接于圆O, , 点D为劣弧上动点,延长 , 交于点E,作交圆O于点F,连接 . (1)、如图1,当点D为弧的中点时,求证:;(2)、如图2,若 , , 试用含有的代数式表示;(3)、在(2)的条件下,若 .
(1)、如图1,当点D为弧的中点时,求证:;(2)、如图2,若 , , 试用含有的代数式表示;(3)、在(2)的条件下,若 .①求证:;
②求的值.