浙江省丽水市松阳县2023年中考二模数学试题
试卷更新日期:2023-06-06 类型:中考模拟
一、单选题
-
1. 如图所示,数的相反数是( )
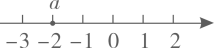 A、-2 B、 C、 D、22. 如图是可移动的3层合唱台阶,其主视图是( )
A、-2 B、 C、 D、22. 如图是可移动的3层合唱台阶,其主视图是( ) A、
A、 B、
B、 C、
C、 D、
D、 3. 在平面直角坐标系中,点P(1,-2)在( )A、第一象限 B、第二象限 C、第三象限 D、第四象限4. 计算的结果是( )A、 B、 C、 D、5. 学校开设了烹饪课程后,某班七名学生学会烹饪的菜品种数依次为;3,5,4,6,3,3,4,则这组数据的众数,中位数分别是( )A、3,3 B、3,4 C、4,3 D、4,46. 如图,树在路灯的照射下形成投影 , 若树离 , 树影 , 树与路灯的水平距离 , 则路灯的高度是( )
3. 在平面直角坐标系中,点P(1,-2)在( )A、第一象限 B、第二象限 C、第三象限 D、第四象限4. 计算的结果是( )A、 B、 C、 D、5. 学校开设了烹饪课程后,某班七名学生学会烹饪的菜品种数依次为;3,5,4,6,3,3,4,则这组数据的众数,中位数分别是( )A、3,3 B、3,4 C、4,3 D、4,46. 如图,树在路灯的照射下形成投影 , 若树离 , 树影 , 树与路灯的水平距离 , 则路灯的高度是( )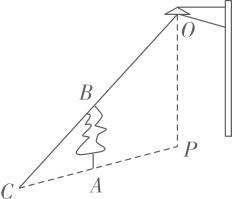 A、3 B、4 C、5 D、67. 近视眼镜的度数(度)与镜片焦距(米)之间有如图所示的反比例函数关系,若配制一副度数小于度的近视眼镜,则焦距的取值范围是( )
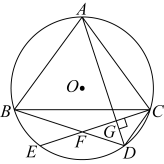
A、3 B、4 C、5 D、67. 近视眼镜的度数(度)与镜片焦距(米)之间有如图所示的反比例函数关系,若配制一副度数小于度的近视眼镜,则焦距的取值范围是( )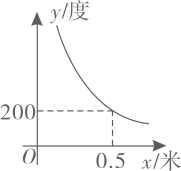 A、 B、 C、 D、8. 某地通信公司调低了长途电话的收费标准,每分钟费用降低了 , 因此按原收费标准6元的通话时间,在新标准下可多通话5分钟.问前后两种收费标准每分钟收费各是多少元?如果设原收费标准每分钟收元,则可列方程( )A、 B、 C、 D、9. 如图是某款“不倒翁”的示意图, , 分别与所在圆相切于点 , . 若该圆半径是 , , 则的长是( )
A、 B、 C、 D、8. 某地通信公司调低了长途电话的收费标准,每分钟费用降低了 , 因此按原收费标准6元的通话时间,在新标准下可多通话5分钟.问前后两种收费标准每分钟收费各是多少元?如果设原收费标准每分钟收元,则可列方程( )A、 B、 C、 D、9. 如图是某款“不倒翁”的示意图, , 分别与所在圆相切于点 , . 若该圆半径是 , , 则的长是( )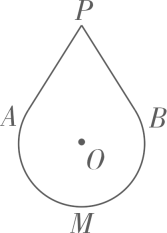 A、 B、 C、 D、10. 如图,在矩形中,交于点 , 点在上,连接分别交 , 于点 , . 若 , 则的值是( )
A、 B、 C、 D、10. 如图,在矩形中,交于点 , 点在上,连接分别交 , 于点 , . 若 , 则的值是( )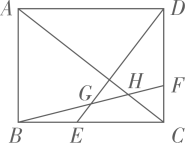 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. 分解因式: .12. 不等式的解集是 .13. 第19届亚运会将于2023年9月23日至10月8日在杭州举行,杭州亚运会吉祥物是“宸宸”,“琮琮”和“莲莲”.将三张正面分别印有以上3个吉样物图案的卡片(卡片的形状,大小,质地都相同)背面朝上,洗匀,若从中任意抽取张,抽得卡片上的图案恰好为“莲莲”的概率是 .
 14. 课堂上,师生一起探究用圆柱形管子的内径去测量球的半径.嘉嘉经过思考找到了测量方法:如图,把球置于圆柱形玻璃瓶上,测得瓶高 , 底面内径 , 球的最高点到瓶底的距离为 , 则球的半径为 .
14. 课堂上,师生一起探究用圆柱形管子的内径去测量球的半径.嘉嘉经过思考找到了测量方法:如图,把球置于圆柱形玻璃瓶上,测得瓶高 , 底面内径 , 球的最高点到瓶底的距离为 , 则球的半径为 . 15. 一副三角板按图放置,是边的中点, . 如图 , 将绕点逆时针旋转,使得点落在线段上不与点重合 , 则的长是 .
15. 一副三角板按图放置,是边的中点, . 如图 , 将绕点逆时针旋转,使得点落在线段上不与点重合 , 则的长是 . 16. 如图,在中, , , 分别是边 , 上的点,且 . 记 , , 的周长分别是 , , .
16. 如图,在中, , , 分别是边 , 上的点,且 . 记 , , 的周长分别是 , , . (1)、若 , 则的值是 .(2)、求的最大值是 .
(1)、若 , 则的值是 .(2)、求的最大值是 .三、解答题
-
17. 计算: .18. 先化简,再求值: , 其中 .19. 如图,是由边长为1的小等边三角形构成的网格,每个小等边三角形的顶点叫作格点.线段AB的端点均在网格上,分别按要求作图,每小题各画出一个即可.
 (1)、在图1中画出以AB为边的平行四边形 , 且点C,D在格点上;(2)、在图2中画出等腰三角形ABE,且点E在格点上;(3)、在图3中画出直角三角形ABF,且点F在格点上.20. 某校为落实“双减”政策及课后服务要求,准备开设乒乓球,素描,书法,篮球,足球五项课后服务项目.为了解学生的需求,学校随机抽取了部分学生进行调查,并将调查结果绘制成如图所示的扇形统计图和条形统计图.请你根据给出的信息解答下列问题:
(1)、在图1中画出以AB为边的平行四边形 , 且点C,D在格点上;(2)、在图2中画出等腰三角形ABE,且点E在格点上;(3)、在图3中画出直角三角形ABF,且点F在格点上.20. 某校为落实“双减”政策及课后服务要求,准备开设乒乓球,素描,书法,篮球,足球五项课后服务项目.为了解学生的需求,学校随机抽取了部分学生进行调查,并将调查结果绘制成如图所示的扇形统计图和条形统计图.请你根据给出的信息解答下列问题: (1)、求m的值,补全条形统计图;(2)、若该校有2000名学生,试估计该校参加“素描”活动的学生有多少人?(3)、结合调查信息,请你给该校开设课后服务项目提出一条合理化的建议.21. 小明出生当天父亲种下一棵山毛榉和一棵枫树.小明6岁生日时,山毛榉,枫树已经分别长到3.3米,2.7米.在此期间,山毛榉的高度(米)和枫树的高度(米)与时间x(年)的函数图象如图所示.请结合图象信息解答下列问题:
(1)、求m的值,补全条形统计图;(2)、若该校有2000名学生,试估计该校参加“素描”活动的学生有多少人?(3)、结合调查信息,请你给该校开设课后服务项目提出一条合理化的建议.21. 小明出生当天父亲种下一棵山毛榉和一棵枫树.小明6岁生日时,山毛榉,枫树已经分别长到3.3米,2.7米.在此期间,山毛榉的高度(米)和枫树的高度(米)与时间x(年)的函数图象如图所示.请结合图象信息解答下列问题: (1)、分别求出与x的函数关系式;(2)、枫树的高度超过山毛榉的高度时,小明的年龄应超过多少岁?22. 某校数学兴趣小组活动:用一张矩形纸片剪出一张菱形纸片,要求菱形的各个顶点均落在矩形的边或顶点上,例如:过矩形两对角线的交点,作两条互相垂直的直线与矩形四边相交,依次连结四个交点,沿连线可剪出菱形.
(1)、分别求出与x的函数关系式;(2)、枫树的高度超过山毛榉的高度时,小明的年龄应超过多少岁?22. 某校数学兴趣小组活动:用一张矩形纸片剪出一张菱形纸片,要求菱形的各个顶点均落在矩形的边或顶点上,例如:过矩形两对角线的交点,作两条互相垂直的直线与矩形四边相交,依次连结四个交点,沿连线可剪出菱形. (1)、请画2种符合要求的示意图;(2)、若 , , 求出你所作的其中一个菱形的边长.
(1)、请画2种符合要求的示意图;(2)、若 , , 求出你所作的其中一个菱形的边长.