浙江省杭州市余杭区2023年中考二模数学试题
试卷更新日期:2023-06-06 类型:中考模拟
一、单选题
-
1. 2023年2月26日,杭州某区最高气温为 , 最低气温为 , 那么这天的最高气温比最低气温高( )A、 B、 C、 D、2. 据统计,2022年北京冬奥会人工造雪面积达到平方米,数用科学记数法表示应为( )A、 B、 C、 D、3. 点A为直线外一点,于点C, . 点P是直线上的动点,则线段长可能是( )A、1 B、3 C、5 D、74. 下列计算正确的是( )A、 B、 C、 D、5. 如图,直线 , 点B在直线a上, , 若∠1=40°,则∠2的度数为( )
 A、40° B、50° C、80° D、140°6. 若点 , 关于原点成中心对称,则a,b的值分别为( )A、 , B、 , C、 , D、 ,7. 某公司本月信誉评分为96分,比上个月的信誉评分提高了 . 设该公司上个月的信誉评分为x.则( )A、 B、 C、 D、8. 如图,正九边形外接圆的半径是R,则这个正九边形的边长为( )
A、40° B、50° C、80° D、140°6. 若点 , 关于原点成中心对称,则a,b的值分别为( )A、 , B、 , C、 , D、 ,7. 某公司本月信誉评分为96分,比上个月的信誉评分提高了 . 设该公司上个月的信誉评分为x.则( )A、 B、 C、 D、8. 如图,正九边形外接圆的半径是R,则这个正九边形的边长为( )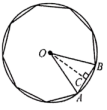 A、 B、 C、 D、9. 如图,在中, , 点P在边上,若是的三等分线,则的长度为( )
A、 B、 C、 D、9. 如图,在中, , 点P在边上,若是的三等分线,则的长度为( )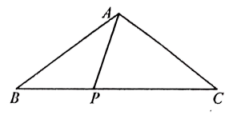 A、或5 B、或 C、或2 D、或210. 已知y关于x的二次函数 , 下列结论中正确的序号是( )
A、或5 B、或 C、或2 D、或210. 已知y关于x的二次函数 , 下列结论中正确的序号是( )①当时,函数图象的顶点坐标为;②当m≠0时,函数图象总过定点:③当时,函数图象在x轴上截得的线段的长度大于;④若函数图象上任取不同的两点、 , 则当时,函数在时一定能使成立.
A、①②③ B、①③④ C、②③④ D、①②④二、填空题
-
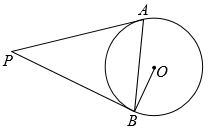
11. 求值: .12. 分解因式: .13. 某校成立了三个课后服务小组,张老师和李老师都报名参加.若随机安排报名人员到服务小组,则他们恰好分到同组的概率是 .14. 如图,PA,PB是的切线,切点分别为A,B,连接OB,AB.如果 , 那么∠P的度数为 .
 15. 如图,在中,的平分线交于点F.点D,E分别在 , 上,连接交于点G.若 , , 则 .
15. 如图,在中,的平分线交于点F.点D,E分别在 , 上,连接交于点G.若 , , 则 . 16. 如图,已知正方形ABCD的边长为1,点M是BC边上的动点(不与B,C重合),点N是AM的中点,过点N作EF⊥AM,分别交AB,BD,CD于点E,K,F,设BM=x.
16. 如图,已知正方形ABCD的边长为1,点M是BC边上的动点(不与B,C重合),点N是AM的中点,过点N作EF⊥AM,分别交AB,BD,CD于点E,K,F,设BM=x. (1)、AE的长为(用含x的代数式表示);(2)、设EK=2KF,则的值为 .
(1)、AE的长为(用含x的代数式表示);(2)、设EK=2KF,则的值为 .三、解答题
-
17. 先化简,再求值: , 其中 .18. 如图,中, , 点D在边上,且交于点E.
 (1)、求证:;(2)、若 , , E是中点,求的长.19. 为调查同学们对亚运知识的了解情况,某校对七八两个年级进行了知识测试(单位:分),从两个年级各随机抽取30名同学的成绩数据,整理并绘制出七年级成绩数据的频数分布直方图(每一组含前一个边界值,不含后一个边界值)和两个年级测试成绩数据统计表.已知七年级这一组的成绩数据为:70 72 73 75 76 77 78 78
(1)、求证:;(2)、若 , , E是中点,求的长.19. 为调查同学们对亚运知识的了解情况,某校对七八两个年级进行了知识测试(单位:分),从两个年级各随机抽取30名同学的成绩数据,整理并绘制出七年级成绩数据的频数分布直方图(每一组含前一个边界值,不含后一个边界值)和两个年级测试成绩数据统计表.已知七年级这一组的成绩数据为:70 72 73 75 76 77 78 78根据以上信息,回答下列问题:
平均数
中位数
众数
七年级
m
80
八年级
72
73
73
 (1)、写出表中m的值.(2)、抽取的测试成绩中,七年级有一个同学A的成绩为75分,八年级恰好也有一位同学B的成绩也是75分,这两名学生在各自年级抽取的测试成绩排名中更靠前的是 , 理由是 .(3)、若七年级共有学生280人,估计七年级所有学生中成绩不低于75分的约有多少人.20. 如图,双曲线上有一点 , 过点A的直线与该双曲线交于点B,且点B的纵坐标为1
(1)、写出表中m的值.(2)、抽取的测试成绩中,七年级有一个同学A的成绩为75分,八年级恰好也有一位同学B的成绩也是75分,这两名学生在各自年级抽取的测试成绩排名中更靠前的是 , 理由是 .(3)、若七年级共有学生280人,估计七年级所有学生中成绩不低于75分的约有多少人.20. 如图,双曲线上有一点 , 过点A的直线与该双曲线交于点B,且点B的纵坐标为1 (1)、求反比例函数和一次函数的解析式.(2)、连接 , 求的面积.(3)、根据图象直接写出在第一象限内一次函数的值大于反比例函数的值时,x的取值范围;21. 如图,在四边形ABCD中, , , 垂足为O,过点D作BD的垂线交BC的延长线于点E.
(1)、求反比例函数和一次函数的解析式.(2)、连接 , 求的面积.(3)、根据图象直接写出在第一象限内一次函数的值大于反比例函数的值时,x的取值范围;21. 如图,在四边形ABCD中, , , 垂足为O,过点D作BD的垂线交BC的延长线于点E. (1)、求证:四边形ACED是平行四边形;(2)、若AC=4,AD=2, , 求BC的长.
(1)、求证:四边形ACED是平行四边形;(2)、若AC=4,AD=2, , 求BC的长.
