广东省中山市2023年中考二模数学试题
试卷更新日期:2023-06-06 类型:中考模拟
一、单选题
-
1. 在- , , 0,-2这四个数中,最小的数是( )A、 B、 C、0 D、-22. 下列运算正确的是( )A、 B、 C、 D、3. 在平面直角坐标系中,二次函数的顶点坐标是
 ( ) A、 B、 C、 D、4. 如图所示的几何体是由四个完全相同的正方体组成的,这个几何体的主视图是
( ) A、 B、 C、 D、4. 如图所示的几何体是由四个完全相同的正方体组成的,这个几何体的主视图是 ( )
( ) A、
A、 B、
B、 C、
C、 D、
D、 5. 如图,△ABC内接于⊙O,∠A=68°,则∠OBC等于( )
5. 如图,△ABC内接于⊙O,∠A=68°,则∠OBC等于( )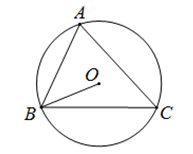 A、22° B、26° C、32° D、34°6. 某校数学兴趣小组在一次数学课外活动中,随机抽查该校10名同学参加今年初中学业水平考试的体育成绩,统计结果如下表所示:
A、22° B、26° C、32° D、34°6. 某校数学兴趣小组在一次数学课外活动中,随机抽查该校10名同学参加今年初中学业水平考试的体育成绩,统计结果如下表所示:成绩(分)
36
37
38
39
40
人数(人)
1
2
1
4
2
表中表示成绩分数的数据中,中位数是( )
A、38分 B、38.5分 C、39分 D、39.5分7. 如图,在中, , , 的垂直平分线交于D,连接 , 若 , 则BC的长为( ) A、 B、 C、 D、8. 关于x的一元二次方程mx2-(m+1)x+1=0有两个不等的整数根,m为整数,那么m的值是( )A、-1 B、1 C、0 D、±19. 祁中初三66班学生毕业时,每个同学都要给其他同学写一份毕业留言作为纪念,全班学生共写了930份留言.如果全班有x名学生,根据题意,列出方程为( )
A、 B、 C、 D、8. 关于x的一元二次方程mx2-(m+1)x+1=0有两个不等的整数根,m为整数,那么m的值是( )A、-1 B、1 C、0 D、±19. 祁中初三66班学生毕业时,每个同学都要给其他同学写一份毕业留言作为纪念,全班学生共写了930份留言.如果全班有x名学生,根据题意,列出方程为( )
A、 =930 B、 =930 C、x(x+1)=930 D、x(x﹣1)=93010. 如图,点为▱的对称中心,轴,与轴交于点 , 与轴交于点 , , 若将绕点顺时针旋转,每次旋转 , 则第2023次旋转结束时,点的坐标为( )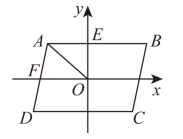 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. 分解因式: = .12. 若分式 有意义,则实数x的取值范围是 .
13. 把103000000用科学记数法表示为 .14. 如图,用一个圆心角为120°的扇形围成一个无底的圆锥,如果这个圆锥底面圆的半径为1 cm,则这个扇形的半径是cm.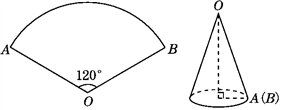 15. 如图,与均为等腰直角三角形,点A,B,E在同一直线上, , 垂足为点B,点C在上, , . 将沿方向平移,当这两个三角形重叠部分的面积等于面积的一半时,平移的距离为 .
15. 如图,与均为等腰直角三角形,点A,B,E在同一直线上, , 垂足为点B,点C在上, , . 将沿方向平移,当这两个三角形重叠部分的面积等于面积的一半时,平移的距离为 .
三、解答题
-
16. 计算:17. 先化简,再求值: , 其中 .18. 如图,已知∠MAN ,点B在射线AM上.
 (1)、尺规作图:
(1)、尺规作图:①在AN上取一点C,使BC=BA;
②作∠MBC的平分线BD.(保留作图痕迹,不写作法)
(2)、在(1)的条件下,求证:BD∥AN.19. 某镇2021年有绿地面积57.5公顷,该镇近几年不断增加绿地面积,2023年达到82.8公顷.(1)、求该镇2021至2023年绿地面积的年平均增长率;(2)、若年平均增长率保持不变,2024年该镇绿地面积能否达到100公顷?20. 如图,已知一次函数的图象与轴、y轴分别交于点A、B两点,且与反比例函数的图象在第一象限内的部分交于点C,垂直于轴于点D,其中 . (1)、求这两个函数的表达式;(2)、若点P在轴上,且 , 求点的坐标.21. 某校设有体育选修课,每位同学必须从羽毛球、篮球、乒乓球、排球、足球五项球类运动中选择一项且只能选择一项球类运动,在该校学生中随机抽取的学生进行调查,根据调查结果绘制成如图所示的尚不完整的频数分布表和扇形统计图.
(1)、求这两个函数的表达式;(2)、若点P在轴上,且 , 求点的坐标.21. 某校设有体育选修课,每位同学必须从羽毛球、篮球、乒乓球、排球、足球五项球类运动中选择一项且只能选择一项球类运动,在该校学生中随机抽取的学生进行调查,根据调查结果绘制成如图所示的尚不完整的频数分布表和扇形统计图.运动项目
频数
羽毛球
30
篮球
兵乓球
36
排球
足球
12

请根据以上图、表信息解答下列问题:
(1)、频数分布表中的 , ;(2)、排球所在的扇形的圆心角为度;(3)、小郭和小李参加上述活动,请用列表或画树状图的方法,求他们恰好参加同一项活动的概率?
