广东省深圳市福田区2023年中考二模数学试卷
试卷更新日期:2023-06-06 类型:中考模拟
一、单选题
-
1. 如图,数轴上点表示的数的相反数是( )
 A、-3 B、 C、2 D、32. 如图,是由相同大小的五个小正方体组成的立体模型,它的俯视图是( )
A、-3 B、 C、2 D、32. 如图,是由相同大小的五个小正方体组成的立体模型,它的俯视图是( ) A、
A、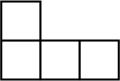 B、
B、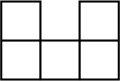 C、
C、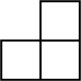 D、
D、 3. 位于深圳市光明中心区科学公园的深圳科技馆占地面积为66000m2 , 66000用科学记数法可以表示成( )A、66×103 B、6.6×104 C、6.6×103 D、0.66×1054. 不等式组的解集是( )A、 B、 C、 D、5. 下列计算正确的是( )A、 B、 C、 D、6. 观察下列尺规作图痕迹,其中所作线段AD为△ABC的角平分线的是( )A、
3. 位于深圳市光明中心区科学公园的深圳科技馆占地面积为66000m2 , 66000用科学记数法可以表示成( )A、66×103 B、6.6×104 C、6.6×103 D、0.66×1054. 不等式组的解集是( )A、 B、 C、 D、5. 下列计算正确的是( )A、 B、 C、 D、6. 观察下列尺规作图痕迹,其中所作线段AD为△ABC的角平分线的是( )A、 B、
B、 C、
C、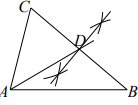 D、
D、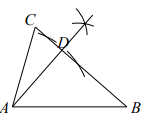 7. 为响应“双减”政策,进一步落实“立德树人、五育并举”的思想主张,深圳某学校积极推进学生综合素质评价改革,小芳在本学期德、智、体、美、劳的评价得分如图所示,其各项的得分分别为9,8,10,8,7,则该同学这五项评价得分的众数,中位数,平均数分别为( )
7. 为响应“双减”政策,进一步落实“立德树人、五育并举”的思想主张,深圳某学校积极推进学生综合素质评价改革,小芳在本学期德、智、体、美、劳的评价得分如图所示,其各项的得分分别为9,8,10,8,7,则该同学这五项评价得分的众数,中位数,平均数分别为( )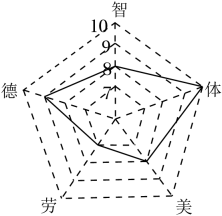 A、8,8,8 B、7,8,7.8 C、8,8,8.7 D、8,8,8.48. 小明用地理中所学的等高线的知识在某地进行野外考察,他根据当地地形画出了“等高线示意图”,如图所示(注:若某地在等高线上,则其海拔就是其所在等高线的数值;若不在等高线上,则其海拔在相邻两条等高线的数值范围内),若点 , , 三点均在相应的等高线上,且三点在同一直线上,则的值为( )
A、8,8,8 B、7,8,7.8 C、8,8,8.7 D、8,8,8.48. 小明用地理中所学的等高线的知识在某地进行野外考察,他根据当地地形画出了“等高线示意图”,如图所示(注:若某地在等高线上,则其海拔就是其所在等高线的数值;若不在等高线上,则其海拔在相邻两条等高线的数值范围内),若点 , , 三点均在相应的等高线上,且三点在同一直线上,则的值为( ) A、 B、 C、 D、29. 我国古代数学经典著作《九章算术》中有这样一题,原文是:今有共买物,人出七,盈二;人出六,不足三.问人数、物价各几何?意思是:今有人合伙购物,每人出七钱,会多二钱;每人出六钱,又差三钱,问人数、货物总价各多少?设人数为x人,货物总价为y钱,可列方程组为( )A、 B、 C、 D、10. 如图,在中, , 点D在斜边上,以为直径的经过边上的点E,连接 , 且平分 , 若的半径为3, , 则线段的长为( )
A、 B、 C、 D、29. 我国古代数学经典著作《九章算术》中有这样一题,原文是:今有共买物,人出七,盈二;人出六,不足三.问人数、物价各几何?意思是:今有人合伙购物,每人出七钱,会多二钱;每人出六钱,又差三钱,问人数、货物总价各多少?设人数为x人,货物总价为y钱,可列方程组为( )A、 B、 C、 D、10. 如图,在中, , 点D在斜边上,以为直径的经过边上的点E,连接 , 且平分 , 若的半径为3, , 则线段的长为( )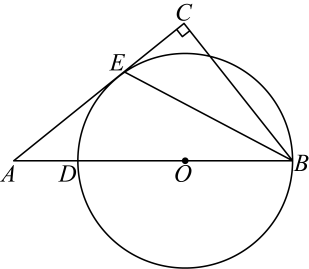 A、 B、8 C、 D、
A、 B、8 C、 D、二、填空题
-
11. 因式分解:a3-a=.12. 一个不透明的袋中装有2个红球和4个黄球,这些球除颜色外完全相同.从袋中随机摸出一个球,摸到黄球的概率是 .
13. 某城市几条道路的位置关系如图所示,道路 , 道路与的夹角 . 城市规划部门想新修一条道路BF,要求 , 则的度数为 . 14. 如图,在平面直角坐标系中,将菱形向右平移一定距离后,顶点C,D恰好均落在反比例函数( , )的图象上,其中点 , , 且轴,则 .
14. 如图,在平面直角坐标系中,将菱形向右平移一定距离后,顶点C,D恰好均落在反比例函数( , )的图象上,其中点 , , 且轴,则 . 15. 如图,正方形的边长为8,对角线相交于点O,点M,N分别在边上,且 , 连接交于P,若 , 则 .
15. 如图,正方形的边长为8,对角线相交于点O,点M,N分别在边上,且 , 连接交于P,若 , 则 .
三、解答题
-
16. 计算:17. 先化简,再求值: , 其中a=3.18. “读书让生活更加多彩,阅读让城市更有温度”.近年来,作为深圳中心城区和“首善之区”的福田各学校积极打造“阅读永恒、书香满溢”的爱阅之校.为了解今年福田区名初三学生的每天平均课外阅读时间,从中随机抽取若干名学生进行问卷调查,并将调查结果绘制成如下不完整的统计图表,请根据图表中所给的信息,解答下列问题:
组别
时间(小时)
频数(人数)
频率
A
40
0.1
B
a
0.3
C
140
b
D
80
0.2
E
20
0.05
 (1)、表中的 , ;(2)、补全频数分布直方图;(3)、结合调查信息,请你估计今年该区初三学生中,每天课外阅读小于1小时的学生约有多少人?19. 为迎接“五一”国际劳动节,某市政府准备购买紫花风和洋红风两种观花树苗,用来美化某大道沿路两侧景观,在购买时发现,紫花风树苗的单价比洋红风树苗的单价高了50%,用1800元购买紫花风树苗的棵数比用1800元购买洋红风树苗的棵数少10棵.(1)、问紫花风、洋红风两种树苗的单价各是多少元?(2)、现需要购买紫花风、洋红风两种树苗共120棵,且购买的总费用不超过8700元,求至少需要购买多少棵洋红风树苗?20. 如图,已知抛物线与x轴交于点和点B,与y轴交于点 .
(1)、表中的 , ;(2)、补全频数分布直方图;(3)、结合调查信息,请你估计今年该区初三学生中,每天课外阅读小于1小时的学生约有多少人?19. 为迎接“五一”国际劳动节,某市政府准备购买紫花风和洋红风两种观花树苗,用来美化某大道沿路两侧景观,在购买时发现,紫花风树苗的单价比洋红风树苗的单价高了50%,用1800元购买紫花风树苗的棵数比用1800元购买洋红风树苗的棵数少10棵.(1)、问紫花风、洋红风两种树苗的单价各是多少元?(2)、现需要购买紫花风、洋红风两种树苗共120棵,且购买的总费用不超过8700元,求至少需要购买多少棵洋红风树苗?20. 如图,已知抛物线与x轴交于点和点B,与y轴交于点 .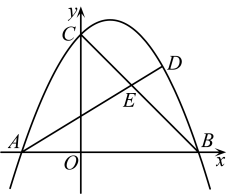 (1)、求该抛物线的表达式;(2)、点E是线段的中点,连接并延长与抛物线交于点D,求点D的坐标.21. 【综合与实践】我国海域的岛屿资源相当丰富,总面积达72800多平方公里,有人居住的岛屿达450个.位于北部湾的某小岛,外形酷似橄榄球,如图1所示.
(1)、求该抛物线的表达式;(2)、点E是线段的中点,连接并延长与抛物线交于点D,求点D的坐标.21. 【综合与实践】我国海域的岛屿资源相当丰富,总面积达72800多平方公里,有人居住的岛屿达450个.位于北部湾的某小岛,外形酷似橄榄球,如图1所示.如图2所示,现把海岸线近似看作直线m,小岛面对海岸线一侧的外缘近似看作 , 经测量,的长可近似为海里,它所对的圆心角的大小可近似为 . (注:在m上的正投影为图中线段 , 点O在m上的正投影落在线段上.)
 (1)、求的半径r;(2)、因该岛四面环海,淡水资源缺乏,为解决岛上居民饮用淡水难的问题,拟在海岸线上,建造一个淡水补给站,向岛上居民输送淡水.为节约运输成本,要求补给站到小岛外缘的距离最近(即要求补给站与上的任意一点,两点之间的距离取得最小值);请你依据所学几何知识,在图2中画出补给站位置及最短运输路线(保留画图痕迹,并做必要标记与注明;不限于尺规作图,不要求证明).(3)、如图3,若测得长为600海里,长为500海里,试求出(2)中的最小距离.22. 【材料阅读】在等腰三角形中,我们把底边与腰长的比叫做顶角的张率 . 如图1,在中, , 顶角的张率记作底边腰 . 容易知道一个角的大小与这个角的张率也是相互唯一确定的,所以,类比三角函数,我们可按上述方式定义的张率,例如, , , 请根据材料,完成以下问题:
(1)、求的半径r;(2)、因该岛四面环海,淡水资源缺乏,为解决岛上居民饮用淡水难的问题,拟在海岸线上,建造一个淡水补给站,向岛上居民输送淡水.为节约运输成本,要求补给站到小岛外缘的距离最近(即要求补给站与上的任意一点,两点之间的距离取得最小值);请你依据所学几何知识,在图2中画出补给站位置及最短运输路线(保留画图痕迹,并做必要标记与注明;不限于尺规作图,不要求证明).(3)、如图3,若测得长为600海里,长为500海里,试求出(2)中的最小距离.22. 【材料阅读】在等腰三角形中,我们把底边与腰长的比叫做顶角的张率 . 如图1,在中, , 顶角的张率记作底边腰 . 容易知道一个角的大小与这个角的张率也是相互唯一确定的,所以,类比三角函数,我们可按上述方式定义的张率,例如, , , 请根据材料,完成以下问题:如图2,是线段上的一动点(不与点 , 重合),点 , 分别是线段 , 的中点,以 , , 为边分别在的同侧作等边三角形 , , , 连接和 .
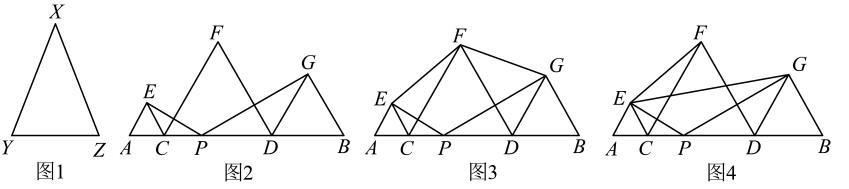 (1)、【理解应用】①若等边三角形 , , 的边长分别为 , , , 则 , , , 三者之间的关系为;
(1)、【理解应用】①若等边三角形 , , 的边长分别为 , , , 则 , , , 三者之间的关系为;②;
(2)、【猜想证明】如图3,连接 , , 猜想的值是多少,并说明理由;(3)、【拓展延伸】如图4,连接 , , 若 , , 则的周长是多少?此时的长为多少?(可直接写出上述两个结果)