广东省汕尾市2023年中考二模数学试题
试卷更新日期:2023-06-06 类型:中考模拟
一、单选题
-
1. 我国两千多年前就开始使用负数,是世界上最早使用负数的国家之一,-2023的相反数是( )A、2023 B、-2023 C、 D、2. 下列四句话中的文字有三句具有对称规律,其中没有这种规律的一句是( )A、上海自来水来自海上 B、有志者事竟成 C、清水池里池水清 D、蜜蜂酿蜂蜜3. 2012年9月25日我国第一艘航母辽宁舰交付海军使用,自此我国航母技术发展迅猛,第三艘航空母舰福建舰于2022年6月17日在中国船舶集团有限公司江南造船厂举行下水命名仪式,福建舰是我国完全自主设计建造的首艘弹射型航空母舰,满载排水量8万吨,这个数据用科学记数法表示为( )吨.A、 B、 C、 D、4. 在下面的四个几何体中,主视图是三角形的是( )A、
 B、
B、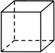 C、
C、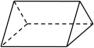 D、
D、 5. 下列各式运算正确的是( )A、 B、 C、 D、6. 计算结果为( )A、 B、 C、 D、7. 如图,一个含有角的直角三角尺的两个顶点放在直尺的对边上,如果 , 那么的度数是( )
5. 下列各式运算正确的是( )A、 B、 C、 D、6. 计算结果为( )A、 B、 C、 D、7. 如图,一个含有角的直角三角尺的两个顶点放在直尺的对边上,如果 , 那么的度数是( ) A、 B、 C、 D、8. 如图①,从边长为a的正方形中剪去一个边长为b的小正方形,然后将剩余分剪拼成一个长方形(如图②),则上述操作所能验证的公式是( )
A、 B、 C、 D、8. 如图①,从边长为a的正方形中剪去一个边长为b的小正方形,然后将剩余分剪拼成一个长方形(如图②),则上述操作所能验证的公式是( ) A、 B、 C、 D、9. 如图,正方形的边长为 , 点F为对角线上一点,当时,则的长是( )
A、 B、 C、 D、9. 如图,正方形的边长为 , 点F为对角线上一点,当时,则的长是( ) A、 B、 C、 D、10. 如图,在的正方形网格中(小正方形的连长为1),有6个点A、B、C、D、E、F,若过A、B、C三点作圆O,则点D、E、F三点中在圆O外的有( )个
A、 B、 C、 D、10. 如图,在的正方形网格中(小正方形的连长为1),有6个点A、B、C、D、E、F,若过A、B、C三点作圆O,则点D、E、F三点中在圆O外的有( )个 A、0 B、1 C、2 D、3
A、0 B、1 C、2 D、3二、填空题
-
11. 式子有意义,则x的取值范围是 .12. 因式分解:m2-3m= .13. 如图在边长相同的小正方形组成的网格中,点A、B、O在小正方形的顶点上,则 .
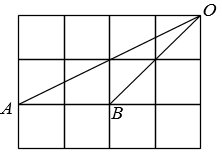 14. 已知 , ( )是一元二次方程 的两个实数根,则代数式 的值为 .15. 如图, , , , , 点M、D、E分别位于上, , 且 , 则 .
14. 已知 , ( )是一元二次方程 的两个实数根,则代数式 的值为 .15. 如图, , , , , 点M、D、E分别位于上, , 且 , 则 .
三、解答题
-
16. 解方程组:17. 已知(1)、化简A;(2)、若x是3的绝对值,求A的值.18. 如图,四边形为矩形.
 (1)、求作边的中点E(用尺规作图法,保留作图痕迹,不要求写作法)(2)、连接、 , 求证 .19. 劳动教育具有树德、增智、强体、育美的综合育人价值,有利于学生树立正确的劳动价值观.某学校为了解学生参加家务劳动的情况,随机抽取了m名学生在某个休息日做家务的劳动时间作为样本,并绘制了以下不完整的频数分布表和扇形统计图.根据题中已有信息,解答下列问题:
(1)、求作边的中点E(用尺规作图法,保留作图痕迹,不要求写作法)(2)、连接、 , 求证 .19. 劳动教育具有树德、增智、强体、育美的综合育人价值,有利于学生树立正确的劳动价值观.某学校为了解学生参加家务劳动的情况,随机抽取了m名学生在某个休息日做家务的劳动时间作为样本,并绘制了以下不完整的频数分布表和扇形统计图.根据题中已有信息,解答下列问题:劳动时间t(单位:小时)
频数
12
a
28
16
4

A∶
B∶
C∶
D∶
E∶
(1)、 , ;(2)、若该校学生有640人,试估计劳动时间在范围的学生有多少人?(3)、劳动时间在范围的4名学生中有男生1名,女生3名,学校准备从中任意抽取2名交流劳动,求抽取的2名学生恰好是一名男生和一名女生的概率.20. 如图,一次函数的图像与双曲线在第一象限交于点 , 在第三象限交于点B. (1)、求反比例函数的解析式;(2)、点P为x轴上的一点,连接 , 若 , 求点P的坐标.21. 某超市销售A、B两款保温杯,已知B款保温杯的销售单价比A款保温杯多10元,用480元购买B款保温杯的数量与用360元购买A款保温杯的数量相同.(1)、A、B两款保温杯的销售单价各是多少元?(2)、由于需求量大,A、B两款保温杯很快售完,该超市计划再次购进这两款保温杯共120个,且A款保温杯的数量不少于B款保温杯数量的两倍.若A款保温杯的销售单价不变,B款保温杯的销售单价降低10%,两款保温杯的进价每个均为20元,应如何进货才能使这批保温杯的销售利润最大,最大利润是多少元?
(1)、求反比例函数的解析式;(2)、点P为x轴上的一点,连接 , 若 , 求点P的坐标.21. 某超市销售A、B两款保温杯,已知B款保温杯的销售单价比A款保温杯多10元,用480元购买B款保温杯的数量与用360元购买A款保温杯的数量相同.(1)、A、B两款保温杯的销售单价各是多少元?(2)、由于需求量大,A、B两款保温杯很快售完,该超市计划再次购进这两款保温杯共120个,且A款保温杯的数量不少于B款保温杯数量的两倍.若A款保温杯的销售单价不变,B款保温杯的销售单价降低10%,两款保温杯的进价每个均为20元,应如何进货才能使这批保温杯的销售利润最大,最大利润是多少元?

