广东省汕头市潮南区陈店镇2023年中考二模数学试题
试卷更新日期:2023-06-06 类型:中考模拟
一、单选题
-
1. 计算:的结果是( )A、0 B、-2 C、2 D、42. 已知某细菌直径长约0.0000202米,那么该细菌的直径长用科学记数法可表示为( )A、米 B、米 C、米 D、米3. 美术老师布置同学们设计窗花,下列作品为轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 4. 图中几何体的三视图是( )
4. 图中几何体的三视图是( )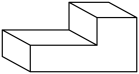 A、
A、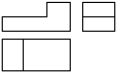 B、
B、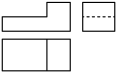 C、
C、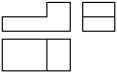 D、
D、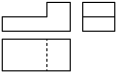 5. 下列运算正确的是( )A、 B、 C、 D、6. 下列说法正确的是( )A、调查某班学生的视力情况适合采用随机抽样调查的方法 B、声音在真空中传播的概率是100% C、甲、乙两名射击运动员10次射击成绩的方差分别是 , , 则甲的射击成绩比乙的射击成绩稳定 D、8名同学每人定点投篮6次,投中次数统计如下:5,4,3,5,2,4,1,5,则这组数据的中位数和众数分别是4和57. 如图,已知是的直径,于点 , , 则( )
5. 下列运算正确的是( )A、 B、 C、 D、6. 下列说法正确的是( )A、调查某班学生的视力情况适合采用随机抽样调查的方法 B、声音在真空中传播的概率是100% C、甲、乙两名射击运动员10次射击成绩的方差分别是 , , 则甲的射击成绩比乙的射击成绩稳定 D、8名同学每人定点投篮6次,投中次数统计如下:5,4,3,5,2,4,1,5,则这组数据的中位数和众数分别是4和57. 如图,已知是的直径,于点 , , 则( ) A、 B、 C、 D、8. 如图,在边长为1的小正方形组成的网格中,A,B,C,D四个点均在格点上,与相交于点E,连接 , 则与的周长比为( )
A、 B、 C、 D、8. 如图,在边长为1的小正方形组成的网格中,A,B,C,D四个点均在格点上,与相交于点E,连接 , 则与的周长比为( )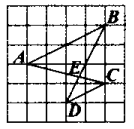 A、1:4 B、4:1 C、1:2 D、2:19. 如图,正方形ABCD的面积为3,点E在边CD上, 且CE = 1,∠ABE的平分线交AD于点F,点M,N分别是BE,BF的中点,则MN的长为( )
A、1:4 B、4:1 C、1:2 D、2:19. 如图,正方形ABCD的面积为3,点E在边CD上, 且CE = 1,∠ABE的平分线交AD于点F,点M,N分别是BE,BF的中点,则MN的长为( )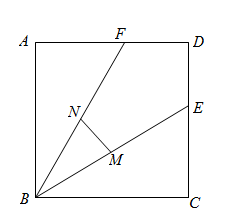 A、 B、 C、 D、10. 已知二次函数的图象如图所示,有下列结论:①;②;③;④ , ⑤ . 其中,正确结论的有( ).
A、 B、 C、 D、10. 已知二次函数的图象如图所示,有下列结论:①;②;③;④ , ⑤ . 其中,正确结论的有( ). A、①②③ B、②③⑤ C、①②④ D、①②③⑤
A、①②③ B、②③⑤ C、①②④ D、①②③⑤二、填空题
-
11. 如图,已知直线AB∥CD,∠1=60°,∠2=45°,则∠CBD的度数为 .
 12. 要使代数式 有意义,x的取值范围是 .13. 把式子化到最简其结果为 .14. 如图,从一个边长是的正五边形纸片上剪出一个扇形,这个扇形的面积为(用含的代数式表示)
12. 要使代数式 有意义,x的取值范围是 .13. 把式子化到最简其结果为 .14. 如图,从一个边长是的正五边形纸片上剪出一个扇形,这个扇形的面积为(用含的代数式表示) 15. 如图,ΔABC是边长为1的等边三角形,分别取AC,BC边的中点D,E,连接DE,作得到四边形EDAF,它的周长记作C1;分别取EF,BE的中点D1 , E1连接D1E1 , 作 , 得到四边形E1D1FF1 , 它的周长记作C2 , 照此规律作下去,则C2021等于 .
15. 如图,ΔABC是边长为1的等边三角形,分别取AC,BC边的中点D,E,连接DE,作得到四边形EDAF,它的周长记作C1;分别取EF,BE的中点D1 , E1连接D1E1 , 作 , 得到四边形E1D1FF1 , 它的周长记作C2 , 照此规律作下去,则C2021等于 .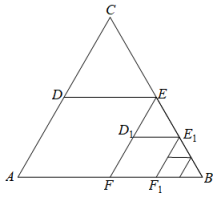
三、解答题
-
16. 计算:
.
17. 如图,一次函数y= kx+b与反比例函数y= 的图象交于A(-2,1)、B(1,a)两点. (1)、分别求出反比例函数与一次函数的关系式;(2)、观察图象,直接写出当反比例函数值大于一次函数值时x的取值范围;18. 如图,在△ABC中,AB=AC=8cm.
(1)、分别求出反比例函数与一次函数的关系式;(2)、观察图象,直接写出当反比例函数值大于一次函数值时x的取值范围;18. 如图,在△ABC中,AB=AC=8cm. (1)、作AB的垂直平分线,交AC于点M,交AB于点N;(尺规作图,保留作图痕迹)(2)、在(1)的条件下,连接MB,若△MBC的周长是14cm,求BC的长.19. 有大小两种货车,3辆大货车与4辆小货车一次可以运货18吨,2辆大货车与6辆小货车一次可以运货17吨.(1)、请问1辆大货车和1辆小货车一次可以分别运货多少吨?(2)、目前有33吨货物需要运输,货运公司拟安排大小货车共计10辆,全部货物一次运完,请问货运公司最少安排几辆大货车?20. 为了解某校九年级全体男生1000米跑步的成绩,随机抽取了部分男生进行测试,并将测试成绩分为A、B、C、D四个等级,绘制出如下两幅不完整的统计图表,根据图表信息解答下列问题:
(1)、作AB的垂直平分线,交AC于点M,交AB于点N;(尺规作图,保留作图痕迹)(2)、在(1)的条件下,连接MB,若△MBC的周长是14cm,求BC的长.19. 有大小两种货车,3辆大货车与4辆小货车一次可以运货18吨,2辆大货车与6辆小货车一次可以运货17吨.(1)、请问1辆大货车和1辆小货车一次可以分别运货多少吨?(2)、目前有33吨货物需要运输,货运公司拟安排大小货车共计10辆,全部货物一次运完,请问货运公司最少安排几辆大货车?20. 为了解某校九年级全体男生1000米跑步的成绩,随机抽取了部分男生进行测试,并将测试成绩分为A、B、C、D四个等级,绘制出如下两幅不完整的统计图表,根据图表信息解答下列问题:成绩等级频数分布表
成绩等级
频数
A
48
B
20
C
x
D
4
 (1)、表中的x= , 扇形图中表示C的圆心角的度数为度.(2)、甲、乙、丙、丁是A等级中的四名学生,学校决定从这四名学生中随机抽取两名介绍体育锻炼经验,请用列表法或画树状图法,求同时抽到甲和乙两名学生的概率.21. 如图,在中,点O在斜边上,以O为圆心,为半径作圆,分别与 , 相交于点D,E,连接 , 已知 .
(1)、表中的x= , 扇形图中表示C的圆心角的度数为度.(2)、甲、乙、丙、丁是A等级中的四名学生,学校决定从这四名学生中随机抽取两名介绍体育锻炼经验,请用列表法或画树状图法,求同时抽到甲和乙两名学生的概率.21. 如图,在中,点O在斜边上,以O为圆心,为半径作圆,分别与 , 相交于点D,E,连接 , 已知 . (1)、求证:是的切线;(2)、若求的半径.22. 已知在中,P是的中点,B是延长线上的一点,连接 , .
(1)、求证:是的切线;(2)、若求的半径.22. 已知在中,P是的中点,B是延长线上的一点,连接 , . (1)、如图1,若 , 求的长.(2)、过点D作 , 交延长线于点E,如图2所示.若 , , 求证: .23. 如图,抛物线经过点 , 点 , 交轴于点 . 连接 , . 为上的动点,过点作轴,交抛物线于点 , 交于点 .
(1)、如图1,若 , 求的长.(2)、过点D作 , 交延长线于点E,如图2所示.若 , , 求证: .23. 如图,抛物线经过点 , 点 , 交轴于点 . 连接 , . 为上的动点,过点作轴,交抛物线于点 , 交于点 . (1)、求这条抛物线的表达式;(2)、过点作 , 垂足为点 , 设点的坐标为 , 请用含的代数式表示线段的长,并求出当为何值时有最大值,最大值是多少?(3)、点在运动过程中,是否存在这样的点 , 使得以 , , 为顶点的三角形与相似.若存在,请求出此时点的坐标;若不存在,请说明理由.
(1)、求这条抛物线的表达式;(2)、过点作 , 垂足为点 , 设点的坐标为 , 请用含的代数式表示线段的长,并求出当为何值时有最大值,最大值是多少?(3)、点在运动过程中,是否存在这样的点 , 使得以 , , 为顶点的三角形与相似.若存在,请求出此时点的坐标;若不存在,请说明理由.