广东省南海区、三水区2023年中考二模数学试卷

试卷更新日期：2023-06-06 类型：中考模拟

进入出卷网下载

一、单选题

1. 比-1大4的数是（）

A、-5 B、-3 C、3 D、5

查看试题解析
2. 据旅游部官网消息，2023年春节7天假日，全国国内出游约308000000人次．数据308000000用科学记数法表示为（）

A、 $3.08 \times 1 0^{8}$ B、 $3.08 \times 1 0^{7}$ C、 $30.8 \times 1 0^{7}$ D、 $0.308 \times 1 0^{9}$

查看试题解析
3. 如图，直线c与直线a、b都相交．若 $a ∥ b$ ， $∠ 1 = 60 °$ ，则 $∠ 2 =$ （）

A、 $60 °$ B、 $55 °$ C、 $50 °$ D、 $45 °$

查看试题解析
4. 一个不透明的袋子中装有20个小球，其中12个红球，8个绿球，这些小球除颜色外完全相同．从袋子中随机摸出一个小球，则摸出的小球是红球的概率是（）

A、 $\frac{3}{10}$ B、 $\frac{3}{8}$ C、 $\frac{2}{5}$ D、 $\frac{3}{5}$

查看试题解析
5. 如图，把正方形 $A B C D$ 沿 $E F$ 折叠，点 $A$ 的对应点为点 $A^{'}$ ，点 $B$ 的对应点为点 $B^{'}$ ，若 $∠ 1 = 40 °$ ，则 $∠ A^{^{'}} E F$ 的度数是（）

A、 $100 °$ B、 $110 °$ C、 $115 °$ D、 $120 °$

查看试题解析
6. 下列运算中，正确的是（）

A、 ${(- b^{2})}^{3} = b^{6}$ B、 $a^{3} + a^{3} = a^{6}$ C、 $(x + 2 y) (x - 2 y) = x^{2} - 4 y^{2}$ D、 $2 a^{6} \div a^{2} = 2 a^{3}$

查看试题解析
7. 如图，在 $△ A B C$ 中，点 $D$ ， $E$ 分别是 $A B$ ， $A C$ 的中点，若 $S_{△ A D E} = 3$ ，则 $S_{△ A B C} =$ （）

A、3 B、6 C、9 D、12

查看试题解析
8. 如图，在 $△ A B C$ 中， $∠ A = 30 °$ ， $∠ A C B = 90 °$ ， $B C = 4$ ，以点 $A$ 为圆心， $A C$ 长为半径画弧，交 $A B$ 于点 $D$ ，则图中阴影部分的面积是（）

A、 $8 \sqrt{3} - 4 π$ B、 $8 \sqrt{3} - 2 π$ C、 $16 \sqrt{3} - 8 π$ D、 $16 \sqrt{3} - 4 π$

查看试题解析
9. 如图，在平面直角坐标系 $x O y$ 中，四边形 $O A B C$ 是菱形， $∠ A O C = 60 °$ ，点 $A$ 坐标为 $(6 ， 0)$ ，将菱形 $O A B C$ 绕原点 $O$ 顺时针旋转 $180 °$ ，旋转后点 $B$ 的坐标为（）

A、 $(9 ， 3 \sqrt{3})$ B、 $(- 9 ， - 3 \sqrt{3})$ C、 $(9 ， - 3 \sqrt{3})$ D、 $(3 \sqrt{3} ， - 9)$

查看试题解析
10. 已知闭合电路的电压为定值，电流 $I (A)$ 与电路的电阻 $R (Ω)$ 是反比例函数关系，根据下表判断以下选项正确的是（）
$I$ （A）
5
$⋯$
$a$
$⋯$
$⋯$
$⋯$
$b$
$⋯$
$⋯$
$R$ （Ω）
20
30
40
50
60
70
80
90
100

A、 $I$ 与 $R$ 的关系式为 $I = \frac{R}{100}$ B、 $I$ 与 $R$ 的关系式为 $I = 20 R$ C、 $a < b$ D、当 $2 < I < a$ 时， $40 < R < 50$

查看试题解析

二、填空题

11. 如果一个数的平方根是 $\pm 8$ ，那么这个数是．

查看试题解析
12. 当 $x =$ 时，代数式 $2 x - 2$ 的值与代数式 $3 x + 3$ 的值相等．

查看试题解析
13. 已知一个多边形的外角和等于其内角和的 $\frac{2}{3}$ ，则这个多边形的边数为.

查看试题解析
14. 已知 $| a - 1 | + {(b + 3)}^{2} + \sqrt{c - 4} = 0$ ，则 $a + b - c =$ ．

查看试题解析
15. 如图，在矩形 $A B C D$ 中， $D C = 3$ ， $A D = \sqrt{3}$ ， $A C$ 的垂直平分线分别交 $A B$ ， $A C$ ， $D C$ 于点 $E$ ， $O$ ， $F$ ，点 $G$ 是 $A E$ 的中点，连接 $A F$ ， $C E$ ， $O G$ ，则下列结论：① $D F = 1$ ；② $O G = \frac{1}{2} B C$ ；③四边形 $A E C F$ 是菱形；④ $S_{△ A O G} = \frac{1}{12} S_{矩形 A B C D}$ ．其中结论正确的是．（请将正确结论的序号填写在横线上）

查看试题解析

三、解答题

16. 解不等式组： ${\begin{array}{l} 3 (x - 1) - x \geq - 5 \\ \frac{2 x + 3}{5} < \frac{x - 1}{2} \end{array}$

查看试题解析
17. 先化简，再求值： $(1 - \frac{1}{x + 1}) \div \frac{x}{x^{2} + 2 x + 1}$ ，其中 $x = 2023$ ．

查看试题解析
18. 如图， $R t △ A B C$ 中， $∠ B A C = 90 °$ ， $A B = A C$ ，点 $D$ ， $E$ 分别在边 $B C$ ， $A B$ 上，连接 $A D$ ， $D E$ ， $∠ A D E = 45 °$ ， $∠ C A D = 22.5 °$ ， $D A = D E$ ．求证： $C D = B E$ ．

查看试题解析
19. “佛山50公里徒步活动”是由佛山市文旅局、文明办主办，媒体推动的体育盛事．某公司为鼓励员工快乐健身，对500名员工的参与情况进行调查，从中抽取了部分员工行走路程（无参与记为 $0 k m$ ，全程参与记为 $50 k m$ ）进行统计．根据统计结果，绘制了如图所示的尚未完成的频率分布表和频数分布直方图．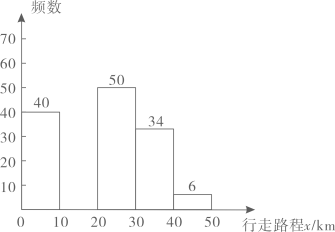
组别
行走路程 $x / k m$
频数
频率
1
$0 \leq x \leq 10$
40
0.2
2
$10 < x \leq 20$
$a$
0.35
3
$20 < x \leq 30$
50
0.25
4
$30 < x \leq 40$
34
0.17
5
$40 < x \leq 50$
6
$b$
根据图表中信息，解答下列问题：

(1)、抽取的员工共有人，频率分布表中 $b =$ ，中位数所在的组别是；

(2)、补全频数分布直方图；

(3)、若对公司行走路程在 $20 k m$ 以下（含 $20 k m$ ）的员工进行激励，增强其运动意识，则预计这部分员工约有多少名？

查看试题解析
20. 电影《流浪地球2》讲述了太阳即将毁灭，人类在地球表面建造出巨大的推进器，以便寻找新的家园，然而宇宙之路危机四伏，为了拯救地球，流浪地球时代的年轻人再次挺身而出，展开争分夺秒的生死之战的故事.2023年元宵节，某电影院开展“弘扬家国情怀，彰显中华气魄”系列活动，对团体购买《流浪地球2》电影票实行优惠，决定在原定零售票价基础上每张降价20元，这样按原定零售票价需花费3000元购买的门票，现在只花费了1800元．

(1)、求每张电影票的原定零售票价；

(2)、为了促进消费，该影院决定对网上购票的个人也采取优惠，原定零售票价经过连续两次降价后票价为每张32元，求平均每次降价的百分率．

查看试题解析
21. 如图，一次函数 $y = k x + b$ 的图象与 $y$ 轴交于点 $A$ ，与反比例函数 $y = \frac{m}{x}$ 的图象交于点 $B (1 ， a)$ 和点 $C (3 ， 2)$ ，连接 $O B$ ， $O C$ ．

(1)、求 $t a n ∠ A O B$ 的值；

(2)、求 $△ B O C$ 的面积．

查看试题解析
22. 如图， $⊙ O$ 是边长为3的等边 $△ A B C$ 的外接圆， $D$ 为 $⊙ O$ 外的一点， $A D ∥ B C$ ，连接 $B D$ 交边 $A C$ 于点 $F$ ，交 $⊙ O$ 于点 $E$ ，连接 $A E$ ， $C E$ ．

(1)、求证： $∠ A B C = ∠ A E B$ ；

(2)、求证： $A D$ 是 $⊙ O$ 的切线；

(3)、当 $A D = \frac{1}{2} A B$ 时，求 $E F$ 的长．

查看试题解析
23. 已知抛物线 $y = a x^{2} + b x + 3$ 经过点 $A (1 ， 0)$ 和点 $B (- 3 ， 0)$ ，与 $y$ 轴交于点 $C$ ．

(1)、求该抛物线的表达式；

(2)、如图1，在对称轴上是否存在一点 $E$ ，使 $△ A E C$ 的周长最小．若存在，请求出点 $E$ 的坐标和 $△ A E C$ 周长的最小值；若不存在，请说明理由；

(3)、如图2，设点 $P$ 是对称轴左侧该抛物线上的一点，点 $Q$ 在对称轴上，当 $△ B P Q$ 为等边三角形时，请直接写出符合条件的直线 $A P$ 的函数表达式．

查看试题解析

$I$ （A）	5	$⋯$	$a$	$⋯$	$⋯$	$⋯$	$b$	$⋯$	$⋯$
$R$ （Ω）	20	30	40	50	60	70	80	90	100

组别	行走路程 $x / k m$	频数	频率
1	$0 \leq x \leq 10$	40	0.2
2	$10 < x \leq 20$	$a$	0.35
3	$20 < x \leq 30$	50	0.25
4	$30 < x \leq 40$	34	0.17
5	$40 < x \leq 50$	6	$b$