广东省广州市天河区2023年中考二模数学试卷

试卷更新日期：2023-06-06 类型：中考模拟

进入出卷网下载

一、单选题

1. 下列四个选项中，为无理数的是（）

A、0 B、3.14 C、-1 D、 $\sqrt{3}$

查看试题解析
2. 2022年1月17日，国务院新闻办公室公布：截至2021年末全国人口总数为141260万，比上年末增加48万人，中国人口的增长逐渐缓慢.141260用科学记数法可表示为（）

A、 $0.14126 \times 10^{6}$ B、 $1.4126 \times 10^{6}$ C、 $1.4126 \times 10^{5}$ D、 $14.126 \times 10^{4}$

查看试题解析
3. 在5轮“中国汉字听写大赛”选拔赛中，甲、乙两位同学的平均分都是90分，甲的成绩方差是15，乙的成绩的方差是3，下列说法正确的是（）

A、甲的成绩比乙的成绩稳定 B、乙的成绩比甲的成绩稳定 C、甲、乙两人的成绩一样稳定 D、无法确定甲、乙的成绩谁更稳定

查看试题解析
4. 方程 $\frac{1}{2 + x} = \frac{2}{3 x - 1}$ 的解为（）

A、 $x = 5$ B、 $x = 3$ C、 $x = 1$ D、 $x = 2$

查看试题解析
5. 下列运算正确的是（）．

A、 $x^{2} \cdot x^{3} = x^{6}$ B、 $2 + \sqrt{5} = 2 \sqrt{5}$ C、 ${(a - 2)}^{2} = a^{2} - 4$ D、 $2^{- 3} = \frac{1}{8}$

查看试题解析
6. 如图，四边形 $A B C D$ 内接于 $⊙ O ， A B = B C$ ，连接 $O A$ ， $O B$ ，若 $∠ B A O = 70 °$ ，则 $∠ D =$ （）

A、 $40 °$ B、 $60 °$ C、 $45 °$ D、 $30 °$

查看试题解析
7. 下列命题中，是真命题的有（）．
①全等三角形的对应边相等；②有两个角为 $60 °$ 的三角形一定是等边三角形；③两条直线被第三条直线所截，内错角相等；④等腰三角形的角平分线和中线相互重合．

A、1个 B、2个 C、3个 D、4个

查看试题解析
8. 已知点 $(2 ， y_{1}) ， (3 ， y_{2})$ 在反比例函数 $y = \frac{- k^{2} - 1}{x}$ 的图象上，则下列结论正确的是（）

A、 $y_{1} > y_{2}$ B、 $y_{1} < y_{2}$ C、 $y_{1} = y_{2}$ D、 $y_{1}$ 和 $y_{2}$ 的大小不能确定

查看试题解析
9. 已知抛物线 $y = a x^{2} + b x$ 开口向下，且经过第三象限的点 $P (- 1 ， m)$ ，若点 $P$ 与原点在抛物线对称轴的异侧，则一次函数 $y = (a - b) x + b$ 的图像不经过（）

A、第一象限 B、第二象限 C、第三象限 D、第四象限

查看试题解析
10. 定义：不大于实数x的最大整数称为x的整数部分，记作 $[x]$ ，例如 $[3.6] = 3 ， [- \sqrt{3}] = - 2$ ，按此规定，若 $[\frac{1 - 3 x}{2}] = - 1$ ，则x的取值范围为（）

A、 $\frac{1}{3} < x \leq 1$ B、 $\frac{1}{3} \leq x < 1$ C、 $1 < x \leq \frac{3}{5}$ D、 $1 \leq x < \frac{5}{3}$

查看试题解析

二、填空题

11. 若 $\sqrt{x - 2}$ 有意义，则实数 $x$ 的取值范围是．

查看试题解析
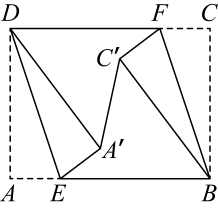
12. 一个圆锥的侧面积为 $6 π$ ，底面圆半径为2，则该圆锥的母线长为．

查看试题解析
13. 一个多边形的每一个外角都等于60°，则这个多边形的内角和为°.

查看试题解析
14. 已知一根弹簧在不挂重物时长6cm，在一定的弹性限度内，每挂1kg重物弹簧伸长0.3cm. 则该弹簧总长y(cm)随所挂物体质量x(kg)变化的函数关系式为.

查看试题解析
15. 若关于x的一元二次方程 $a x^{2} - x - \frac{1}{4} = 0 (a \neq 0)$ 有两个不相等的实数根，则点 $P (a + 1, - a - 3)$ 在第象限．

查看试题解析
16. 如图，四边形 $A B C D$ 为矩形， $A B = 8 ， A D = 6$ ，点E，F分别为边 $A B$ ， $C D$ 上动点，且 $A E = C F$ ，连接 $D E$ ， $B F$ ，分别将 $△ D A E$ 和 $△ B C F$ 沿 $D E$ ， $B F$ 翻折，点A的对应点为点 $A ′$ ，点C的对应点为点 $C^{'}$ ，连接 $A^{'} C^{'}$ ，当点 $A^{'} ， C^{'}$ 均落在矩形 $A B C D$ 的同一条对角线上时， $A E$ 长为．

查看试题解析

三、解答题

17. 解方程组： ${\begin{array}{l} x - y = 1 \\ 2 x + y = 5 \end{array}$

查看试题解析
18. 如图，已知AB＝AD，AC＝AE，∠1＝∠2，求证：△ABC≌△ADE．

查看试题解析

19. 某中学为了解学生每学期“诵读经典”的情况，在全校范围内随机抽查了部分学生第一学期阅读量，学校将阅读量分成优秀、良好、较好、一般四个等级，抽查情况如下表：

等级	一般	较好	良好	优秀
阅读量/本	3	4	5	6
频数	12	20	14	4

请根据统计表中提供的信息，解答下列问题：

(1)、所抽查学生阅读量的众数为，中位数为；

(2)、样本数据中优秀等级学生有4人，其中仅有

1

名男生．现从中任选派2名学生去参加读书分享会，请用树状图法或列表法求所选2名同学中有男生的概率．

查看试题解析

20. 某校九年级组织各班级（每班人数都大于40但不超过50）同学观看励志电影，由各班班长负责买票，票价为每张40元．在询问买团体票的优惠情况时，售票员说：“40人以上的团体票有两个优惠方案可选择：方案一是全班同学打7折；方案二是班级中可有6人免费，剩余同学打8折．”

(1)、填空：若三班班长说：“我们班无论选择何种方案，付的钱数都是一样的．”那么，三班人数为；

(2)、若二班班长通过比较发现，确定二班采用方案一比较优惠，求二班的人数．

查看试题解析
21. 已知代数式 $A = (\frac{m^{2}}{m - 2} - \frac{2 m}{m - 2}) + (m - 3) (2 m + 1)$ ．

(1)、化简A；

(2)、若m是方程 $x^{2} - 2 x = 0$ 的根，求A的值．

查看试题解析
22. 已知正方形 $A B C D$ 中， $B C = 3$ ， E是边 $A B$ 上的动点，连接 $A C$ 和 $C E$ ．

(1)、尺规作图：在图中分别作线段 $A C$ 和 $C E$ 的中点F和G，连接FG；（不写作法，不说明理由，写明结论并保留作图痕迹）

(2)、当 $C E = 2 A E$ 时，求（1）中所作的线段 $F G$ 的长度．

查看试题解析
23. 如图，在平面直角坐标系中， $⊙ P$ 与x轴相切于点C，与y轴负半轴分别相交于A，B两点，连接 $A P$ 并延长分别交 $⊙ P$ ， x轴于点D和点E，连接 $D C$ 并延长交y轴的正半轴于点F，已知点D的坐标为 $(12 ， - 2)$ ．

(1)、求点F的坐标：

(2)、求点E的坐标．

查看试题解析
24. 已知函数 $y_{1} = - x^{2} + (m + 2) x - 2 m + 1$ 和函数 $y_{2} = (n + 2) x - 2 n - 3$ ，其中， $m ， n$ 为常数，且 $n \neq - 2$ ，记函数 $y_{1}$ 的顶点为 $P$ ．

(1)、当 $m = 0$ 时，点 $P$ 恰好在函数 $y_{2}$ 的图像上，求 $n$ 的值；

(2)、随着 $m$ 的变化，点 $P$ 是否都在某一条抛物线上？如果是，求出该抛物线的解析式，如果不是，请说明理由；

(3)、当 $- 1 < x < 2$ 时，总有 $y_{2} < y_{1}$ ，求 $m - n$ 的取值范围．

查看试题解析
25. 如图，在菱形 $A B C D$ 中， $A B = 4 ， ∠ B A D = 60 °$ ，点P在边 $A D$ 上，过点P作 $P Q ⊥ A B ， P M ⊥ A D$ ，分别交直线 $A B$ 于点Q，M．

(1)、当点P与点D重合时，求 $M B$ 的长；

(2)、设 $△ P Q M$ 与菱形 $A B C D$ 重叠部分图形的面积为S， $A P = t$ ．当 $1 \leq t \leq 3$ 时，求S的最大值；

(3)、若以线段 $P Q$ 为边，在 $P Q$ 的右侧作等边三角形 $P Q E$ ，当线段 $B E$ 长最小时，求 $c o s ∠ E B A$ 的值．

查看试题解析