广东省东莞市2023年中考二模数学试卷
试卷更新日期:2023-06-06 类型:中考模拟
一、单选题
-
1. 下列实数是无理数的是( )A、-2 B、1 C、 D、22. 某种芯片每个探针单元的面积为 ,0.00000164用科学记数法可表示为( )A、 B、 C、 D、3. 下列立体图形中,俯视图是三角形的是( )A、
 B、
B、 C、
C、 D、
D、 4. 下列计算正确的是( )A、 B、 C、 D、5. 一个多边形的每个外角都等于72°,则这个多边形的边数为( )
4. 下列计算正确的是( )A、 B、 C、 D、5. 一个多边形的每个外角都等于72°,则这个多边形的边数为( )
A、5 B、6 C、7 D、86. 把抛物线向左平移1个单位,然后向下平移3个单位,则平移后抛物线的解析式为( )A、 B、 C、 D、7. 如图,.若 , 则的大小为( )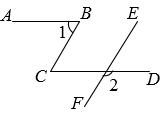 A、 B、 C、 D、8. 在同一平面直角坐标系中,一次函数与反比例函数的图像如图所示、则当时,自变量的取值范围为( )
A、 B、 C、 D、8. 在同一平面直角坐标系中,一次函数与反比例函数的图像如图所示、则当时,自变量的取值范围为( ) A、 B、 C、 D、9. 如图,由边长为1的小正方形构成的网格中,点A,B,C都在格点上,以AB为直径的圆经过点C、D,则 的值为( )
A、 B、 C、 D、9. 如图,由边长为1的小正方形构成的网格中,点A,B,C都在格点上,以AB为直径的圆经过点C、D,则 的值为( )
 A、 B、 C、 D、10. 如图1,在中,点P从点A出发向点C运动,设x表示线段的长,y表示线段的长,下列结论不正确的是( )
A、 B、 C、 D、10. 如图1,在中,点P从点A出发向点C运动,设x表示线段的长,y表示线段的长,下列结论不正确的是( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. 若代数式 有意义,则实数x的取值范围是 .12. 点 关于 轴的对称点是.13. 不等式组 的解集是.14. 如图,把△ABC绕点C顺时针旋转得到△A′B′C,此时A′B′⊥AC于点D,已知∠A=50°,则∠B′CB的度数是 .
 15. 若方程的一个根是m,则代数式 .16. 双曲线 在第一象限的图象如图,过y1上的任意一点A,作x轴的平行线交y2于B,交y轴于C,若S△AOB=3,则k的值为.
15. 若方程的一个根是m,则代数式 .16. 双曲线 在第一象限的图象如图,过y1上的任意一点A,作x轴的平行线交y2于B,交y轴于C,若S△AOB=3,则k的值为. 17. 如图,将等边的三条边向外延长一倍,得到第一个新的 . 第二次将等边的三边向外延长一倍,得到第二个新的 , 依此规律继续延长下去,若的面积 , 则第2023个新的三角形的面积为 .
17. 如图,将等边的三条边向外延长一倍,得到第一个新的 . 第二次将等边的三边向外延长一倍,得到第二个新的 , 依此规律继续延长下去,若的面积 , 则第2023个新的三角形的面积为 .
三、解答题
-
18. 计算:
.
19. 先化简,再求值 , 其中 .20. 如图,已知△ABC,∠C=90°, (1)、请用直尺与圆规作图,作线段AB的垂直平分线,交AB于点E,交BC于点D.(不写作法,但要保留作图痕迹)(2)、若∠B=15°,若AC= , 则BD= .21. 春季开学后,某校为了让学生有效应用压岁钱,开展有意义的“尊老、敬老”慈善捐款活动,将捐款捐赠给本市敬老院.学生会为了了解学生捐款的情况,随机调查了该校部分学生,根据调查结果,绘制了两幅不完整的统计图.请根据相关信息,解答下列问题:
(1)、请用直尺与圆规作图,作线段AB的垂直平分线,交AB于点E,交BC于点D.(不写作法,但要保留作图痕迹)(2)、若∠B=15°,若AC= , 则BD= .21. 春季开学后,某校为了让学生有效应用压岁钱,开展有意义的“尊老、敬老”慈善捐款活动,将捐款捐赠给本市敬老院.学生会为了了解学生捐款的情况,随机调查了该校部分学生,根据调查结果,绘制了两幅不完整的统计图.请根据相关信息,解答下列问题: (1)、本次调查的学生人数为人,在扇形统计图中,捐款金额为100元所在扇形的圆心角的度数是度,在调查的这组学生中,捐款金额的中位数是元;(2)、补全条形统计图;(3)、学生会为了更好地引导学生合理支配压岁钱,选出甲,乙,丙和丁四人从不同的方面在全校进行讲解,但由于时间的限定,临时调整只能两人讲解.因此,学生会采用随机抽签的方式从甲,乙,丙和丁四人中确定两名讲解人选.请用列表或画树状图的方式说明抽中甲和乙的概率是多少?22. 如图,的半径为6cm,经过上一点C作的切线交半径的延长于点B,作的平分线交于点D,交于点F,延长交于点E.
(1)、本次调查的学生人数为人,在扇形统计图中,捐款金额为100元所在扇形的圆心角的度数是度,在调查的这组学生中,捐款金额的中位数是元;(2)、补全条形统计图;(3)、学生会为了更好地引导学生合理支配压岁钱,选出甲,乙,丙和丁四人从不同的方面在全校进行讲解,但由于时间的限定,临时调整只能两人讲解.因此,学生会采用随机抽签的方式从甲,乙,丙和丁四人中确定两名讲解人选.请用列表或画树状图的方式说明抽中甲和乙的概率是多少?22. 如图,的半径为6cm,经过上一点C作的切线交半径的延长于点B,作的平分线交于点D,交于点F,延长交于点E. (1)、求证:;(2)、如果 , 求的长度.23. 某学校计划从商店购买测温枪和洗手液,已知购买一个测温枪比购买一瓶洗手液多用20元,若用400元购买测温枪和用160元购买洗手液,则购买测温枪的个数是购买洗手液个数的一半.(1)、求购买一个测温枪、一瓶洗手液各需要多少元;(2)、经商谈,商店给予该学校购买一个测温枪赠送一瓶洗手液的优惠,如果该学校需要洗手液个数是测温枪个数的2倍还多8个,且该学校购买测温枪和洗手液的总费用不超过670元,那么该学校最多可购买多少个测温枪?
(1)、求证:;(2)、如果 , 求的长度.23. 某学校计划从商店购买测温枪和洗手液,已知购买一个测温枪比购买一瓶洗手液多用20元,若用400元购买测温枪和用160元购买洗手液,则购买测温枪的个数是购买洗手液个数的一半.(1)、求购买一个测温枪、一瓶洗手液各需要多少元;(2)、经商谈,商店给予该学校购买一个测温枪赠送一瓶洗手液的优惠,如果该学校需要洗手液个数是测温枪个数的2倍还多8个,且该学校购买测温枪和洗手液的总费用不超过670元,那么该学校最多可购买多少个测温枪?

