沪科版数学八年级下册19.4四边形最值问题汇编
试卷更新日期:2023-06-05 类型:同步测试
一、单选题
-
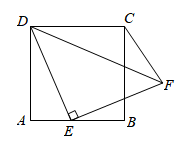
1. 如图,菱形ABCD中,AE=1,AF=BE=2.若P为对角线BD 上一动点,则EP+FP的最小值为( )
 A、1 B、2 C、3 D、42. 如图所示,在菱形ABCD中,AB=6,∠BAD=120°,△AEF为正三角形,点E、F分别在菱形的边BC、CD上滑动,且E、F不与B、C、D重合.当点E、F在BC、CD上滑动时,△CEF的面积最大值是( )
A、1 B、2 C、3 D、42. 如图所示,在菱形ABCD中,AB=6,∠BAD=120°,△AEF为正三角形,点E、F分别在菱形的边BC、CD上滑动,且E、F不与B、C、D重合.当点E、F在BC、CD上滑动时,△CEF的面积最大值是( ) A、4 B、 C、3 D、3. 如图,菱形ABCD的边长为2,且∠ABC=120°,E是BC的中点,P为BD上一点,且△PCE的周长最小,则△PCE的周长的最小值为( )
A、4 B、 C、3 D、3. 如图,菱形ABCD的边长为2,且∠ABC=120°,E是BC的中点,P为BD上一点,且△PCE的周长最小,则△PCE的周长的最小值为( ) A、+1 B、+1 C、2+1 D、2+14. 如图,在菱形 中, 分别是边 的中点,P是对角线 上一动点,已知菱形边长为5,对角线 长为6,则 周长的最小值是( )
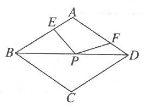
A、+1 B、+1 C、2+1 D、2+14. 如图,在菱形 中, 分别是边 的中点,P是对角线 上一动点,已知菱形边长为5,对角线 长为6,则 周长的最小值是( ) A、11 B、10 C、9 D、85. 如图,菱形ABCD的对角线相交于点O , AC=12,BD=16,点P为边BC上一点,且点P不与点B、C重合.过点P作PE⊥AC于点E , PF⊥BD于点F , 连结EF , 则EF的最小值为( )
A、11 B、10 C、9 D、85. 如图,菱形ABCD的对角线相交于点O , AC=12,BD=16,点P为边BC上一点,且点P不与点B、C重合.过点P作PE⊥AC于点E , PF⊥BD于点F , 连结EF , 则EF的最小值为( )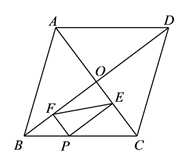 A、4 B、4.8 C、5 D、66. 如图,菱形ABCD中,AB=2,∠A=120°,点P是直线BD上一动点,连接PC,当PC+ 的值最小时,线段PD的长是( )
A、4 B、4.8 C、5 D、66. 如图,菱形ABCD中,AB=2,∠A=120°,点P是直线BD上一动点,连接PC,当PC+ 的值最小时,线段PD的长是( ) A、 B、 C、 D、7. 如图,菱形ABCD的边长为2 ,∠ABC=60°,点E、F在对角线BD上运动,且EF=2,连接AE、AF,则△AEF周长的最小值是( )
A、 B、 C、 D、7. 如图,菱形ABCD的边长为2 ,∠ABC=60°,点E、F在对角线BD上运动,且EF=2,连接AE、AF,则△AEF周长的最小值是( )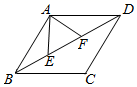 A、4 B、4+ C、2+2 D、68. 如图,在矩形中, , , 动点满足 , 则点到、两点距离之和的最小值为( )
A、4 B、4+ C、2+2 D、68. 如图,在矩形中, , , 动点满足 , 则点到、两点距离之和的最小值为( ) A、 B、 C、 D、9. 如图,正方形ABCD的边长是4,点E是DC上一个点,且DE=1,P点在AC上移动,则PE+PD的最小值是( )
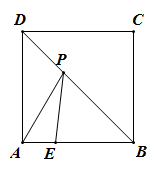
A、 B、 C、 D、9. 如图,正方形ABCD的边长是4,点E是DC上一个点,且DE=1,P点在AC上移动,则PE+PD的最小值是( )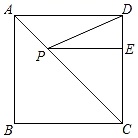 A、4 B、4.5 C、5.5 D、510. 如图,P是边长为1的正方形ABCD的对角线BD上的一点,点E是AB的中点,则PA+PE最小值是( )
A、4 B、4.5 C、5.5 D、510. 如图,P是边长为1的正方形ABCD的对角线BD上的一点,点E是AB的中点,则PA+PE最小值是( )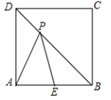 A、 B、 C、 D、11. 如图,在菱形 中, , ,点P是线段AC上一动点,点F是线段AB上一动点,则 的最小值( )
A、 B、 C、 D、11. 如图,在菱形 中, , ,点P是线段AC上一动点,点F是线段AB上一动点,则 的最小值( ) A、 B、3 C、 D、12. 如图,在 ▱ABCD中,CD=2AD,BE⊥AD于点E,F为DC的中点,连结EF、BF,下列结论:①∠ABC=2∠ABF;②EF=BF;③S四边形DEBC=2S△EFB;④∠CFE=3∠DEF,其中符合题意结论的个数共有( ).
A、 B、3 C、 D、12. 如图,在 ▱ABCD中,CD=2AD,BE⊥AD于点E,F为DC的中点,连结EF、BF,下列结论:①∠ABC=2∠ABF;②EF=BF;③S四边形DEBC=2S△EFB;④∠CFE=3∠DEF,其中符合题意结论的个数共有( ). A、1个 B、2个 C、3个 D、4个
A、1个 B、2个 C、3个 D、4个二、填空题
-
13. 如图,正方形ABCD的边长是5,E是边BC上一点且BE=2,F为边AB上的一个动点,连接EF,以EF为边向右作等边三角形EFG,连接CG,则CG长的最小值为.
 14. 如图,已知正方形ABCD的边长为4,点E是AB边上一动点,连接ED,将ED绕点E顺时针旋转90°到EF,连接DF,CF,则DF+CF的最小值是.
14. 如图,已知正方形ABCD的边长为4,点E是AB边上一动点,连接ED,将ED绕点E顺时针旋转90°到EF,连接DF,CF,则DF+CF的最小值是.