吉林省名校调研卷系列(省命题A)2022-2023学年八年级下学期期中数学试卷
试卷更新日期:2023-06-05 类型:期中考试
一、单选题
-
1. 计算的结果是( )A、5 B、-5 C、-25 D、252. 下列二次根式中为最简二次根式的是( )A、 B、 C、 D、3. 下列各组数据中的三个数作为三角形的三边长,其中能构成直角三角形的是( )A、2,3,4 B、5,12,13 C、4,6,8 D、5,12,154. 下列式子计算结果正确的是( )A、 B、 C、 D、5. 如图,在中,平分线交于点E,的平分线交于点F,若 , , 则EF的长( )
 A、1 B、2 C、3 D、46. 如图,在正方形中,E为上一点,连接 , 交对角线于点F,连接 , 若 , 则的度数为( )
A、1 B、2 C、3 D、46. 如图,在正方形中,E为上一点,连接 , 交对角线于点F,连接 , 若 , 则的度数为( ) A、80° B、70° C、75° D、45°
A、80° B、70° C、75° D、45°二、填空题
-
7. 计算: .8. 若代数式 有意义,则实数 的取值范围是.9. 添加一个条件,使矩形ABCD是正方形,这个条件可能是 .10. 如图,在平面直角坐标系中,四边形是菱形,其中点B的坐标是 , 点D的坐标是 , 点A在x轴上,则点C的坐标是 .
 11. 如图,在中相交于点 , , 当时,是矩形.
11. 如图,在中相交于点 , , 当时,是矩形. 12. 如图,在中, , 以和为边向两边分别作正方形,面积分别为和 , 已知 , 则的长为 .
12. 如图,在中, , 以和为边向两边分别作正方形,面积分别为和 , 已知 , 则的长为 . 13. 一个菱形的两条对角线长分别为和 , 则这个菱形的面积是 .14. 在中, , 点N是边上一点,点M为边上的动点,点D、E分别为的中点,则的最小值是 .
13. 一个菱形的两条对角线长分别为和 , 则这个菱形的面积是 .14. 在中, , 点N是边上一点,点M为边上的动点,点D、E分别为的中点,则的最小值是 .
三、解答题
-
15. 计算:16. 计算:17. 计算:18. 如图,四边形 和 都是平行四边形.求证:四边形 是平行四边形.
 19. 如图,在中, , D是上的一点, , 求的长.
19. 如图,在中, , D是上的一点, , 求的长. 20. 如图①、图②均是6×6的正方形网格,每个小正方形的边长均为1,每个小正方形的顶点叫做格点.
20. 如图①、图②均是6×6的正方形网格,每个小正方形的边长均为1,每个小正方形的顶点叫做格点. (1)、在图中画一个面积为10的正方形;(2)、在图②中画一个面积为12的菱形,并直接写出这个菱形的周长.21. 如图,由太原到北京的“和谐号”动车在距离铁轨米的点C处(即米,),当动车车头在点A处时,恰好位于点C处的北偏东的方向上,秒后,动车车头由A处到达点B处,此时测得B,C两点间的距离为米,求这列动车的平均速度.
(1)、在图中画一个面积为10的正方形;(2)、在图②中画一个面积为12的菱形,并直接写出这个菱形的周长.21. 如图,由太原到北京的“和谐号”动车在距离铁轨米的点C处(即米,),当动车车头在点A处时,恰好位于点C处的北偏东的方向上,秒后,动车车头由A处到达点B处,此时测得B,C两点间的距离为米,求这列动车的平均速度.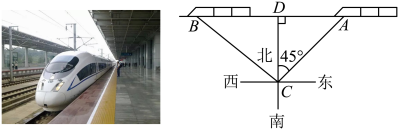 22. 如图,已知的对角线、交于点O,过点O且与分别相交于点 .
22. 如图,已知的对角线、交于点O,过点O且与分别相交于点 . (1)、求证:;(2)、若 , , , 求的长.23. 如图,在中, , 为边上的中线,点E与点D关于直线对称,连接、 .
(1)、求证:;(2)、若 , , , 求的长.23. 如图,在中, , 为边上的中线,点E与点D关于直线对称,连接、 . (1)、求证:四边形是菱形;(2)、连接 , 若 , 则的长为 .24. 如用,在菱形中对角线交于点 . 过点作于点 , 延长到点 , 使 . 连接 .
(1)、求证:四边形是菱形;(2)、连接 , 若 , 则的长为 .24. 如用,在菱形中对角线交于点 . 过点作于点 , 延长到点 , 使 . 连接 . (1)、求证:四边形是矩形;(2)、若 , , 求菱形的周长.25. 【操作一】如图①,对折正方形纸片 , 使与重合,得到折痕 , 把纸片展平.
(1)、求证:四边形是矩形;(2)、若 , , 求菱形的周长.25. 【操作一】如图①,对折正方形纸片 , 使与重合,得到折痕 , 把纸片展平. (1)、【操作二】如图在②上选一点 , 沿折叠,使点落在正方形内部点处,把纸片展平,连接 , 延长交于点 , 连接 . 求证:;
(1)、【操作二】如图在②上选一点 , 沿折叠,使点落在正方形内部点处,把纸片展平,连接 , 延长交于点 , 连接 . 求证:; (2)、【探究】在操作二中,若正方形纸片的边长为 , 求的长.26. 如图在中, , 是边上的高,且的面积为24.动点P、Q分别从点A、C同时出发,均以每秒1个单位长度的速度分别沿、向终点B、D运动,设点P运动的时间为t秒.
(2)、【探究】在操作二中,若正方形纸片的边长为 , 求的长.26. 如图在中, , 是边上的高,且的面积为24.动点P、Q分别从点A、C同时出发,均以每秒1个单位长度的速度分别沿、向终点B、D运动,设点P运动的时间为t秒. (1)、求的长;(2)、求证:四边形是平行四边形;(3)、当四边形是矩形时,求t的值;(4)、当以点A、B、C、D、P、Q中的四个点为顶点的四边形是菱形时,直接写出t的值.
(1)、求的长;(2)、求证:四边形是平行四边形;(3)、当四边形是矩形时,求t的值;(4)、当以点A、B、C、D、P、Q中的四个点为顶点的四边形是菱形时,直接写出t的值.