广东省广州市2023届高三数学冲刺训练(二)试卷
试卷更新日期:2023-06-02 类型:高考模拟
一、单选题
-
1. 复数( )A、 B、 C、 D、2. 已知集合 , 则集合的子集个数为( )A、4 B、3 C、2 D、13. 我国古代《九章算术》将上下两个平行平面为矩形的六面体称为刍童.如图池盆几何体是一个刍童,其中上下底面为正方形边长分别为6和2,侧面是全等的等腰梯形梯形的高为 , 若盆中积水深为池盆高度的一半,则该盆中积水的体积为( )
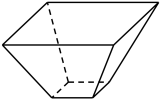 A、 B、 C、 D、4. 已知以为焦点的椭圆与直线有且仅有一个公共点,则椭圆的长轴长为( )A、 B、 C、 D、5. 在中,是边上一点,且是上一点,若 , 则实数的值为( )A、 B、 C、 D、6. 欧拉函数的函数值等于所有不超过正整数 , 且与互素的正整数的个数,例如, , . 若 , 且 , 则( )A、3 B、4 C、5 D、67. 已知正实数满足 , 则的最小值为( )A、2 B、4 C、8 D、98. 已知函数 , 若 , 则实数的取值范围为( )A、 B、 C、 D、
A、 B、 C、 D、4. 已知以为焦点的椭圆与直线有且仅有一个公共点,则椭圆的长轴长为( )A、 B、 C、 D、5. 在中,是边上一点,且是上一点,若 , 则实数的值为( )A、 B、 C、 D、6. 欧拉函数的函数值等于所有不超过正整数 , 且与互素的正整数的个数,例如, , . 若 , 且 , 则( )A、3 B、4 C、5 D、67. 已知正实数满足 , 则的最小值为( )A、2 B、4 C、8 D、98. 已知函数 , 若 , 则实数的取值范围为( )A、 B、 C、 D、二、多选题
-
9. 为了加强疫情防控,某中学要求学生在校时每天都要进行体温检测.某班级体温检测员对一周内甲乙两名同学的体温进行了统计,其结果如图所示,则下列结论正确的是( )
 A、乙同学体温的极差为 B、甲同学体温的中位数与平均数相等 C、乙同学体温的方差比甲同学体温的方差小 D、甲同学体温的第60百分位数为10. 已知函数 , 其图像上相邻的两个最高点之间的距离为在上是单调函数,则下列说法不正确的是( )A、的最大值为 B、在上的图像与直线没有交点 C、在上没有对称轴 D、在上有一个零点11. 函数 , 则下列结论正确的是( )A、若函数在上为减函数,则 B、若函数的对称中心为 , 则 C、当时,若有三个根 , 且 , 则 D、当时,若过点可作曲线的三条切线,则12. 已知正四面体的棱长为分别为正四面体棱的中点,为面内任意一点,则下列结论正确的是( )A、平面截正四面体的外接球所得截面的面积为 B、若存在 , 使得 , 则线段长度的最小值为 C、过点作平面平面 , 若平面平面 , 平面平面 , 则所成角的正弦值为 D、平面与平面夹角的余弦值为
A、乙同学体温的极差为 B、甲同学体温的中位数与平均数相等 C、乙同学体温的方差比甲同学体温的方差小 D、甲同学体温的第60百分位数为10. 已知函数 , 其图像上相邻的两个最高点之间的距离为在上是单调函数,则下列说法不正确的是( )A、的最大值为 B、在上的图像与直线没有交点 C、在上没有对称轴 D、在上有一个零点11. 函数 , 则下列结论正确的是( )A、若函数在上为减函数,则 B、若函数的对称中心为 , 则 C、当时,若有三个根 , 且 , 则 D、当时,若过点可作曲线的三条切线,则12. 已知正四面体的棱长为分别为正四面体棱的中点,为面内任意一点,则下列结论正确的是( )A、平面截正四面体的外接球所得截面的面积为 B、若存在 , 使得 , 则线段长度的最小值为 C、过点作平面平面 , 若平面平面 , 平面平面 , 则所成角的正弦值为 D、平面与平面夹角的余弦值为三、填空题
-
13. 已知且 , 的展开式中存在常数项,写出的一个值为 .14. 已知函数 , 曲线在点处的切线与直线垂直,则 .15. 已知点的坐标为 , 点是圆上任意两个不同的点,且满足 , 设为线段的中点,则的最大值为 .16. 在中随机选取三个数,能构成公差不小于5的等差数列的概率为 .
四、解答题
-
17. 设为数列的前项和,已知 .(1)、求;(2)、求证: .18. 如图,在四棱锥中, , , 点为的中点.
 (1)、求证:平面;(2)、若平面平面 , 求直线与平面所成角的正弦值.19. 某款自营生活平台以及提供配送服务的生活类软件主要提供的产品有水产海鲜,水果,蔬菜,食品,日常用品等.某机构为调查顾客对该软件的使用情况,在某地区随机访问了100人,访问结果如下表所示.
(1)、求证:平面;(2)、若平面平面 , 求直线与平面所成角的正弦值.19. 某款自营生活平台以及提供配送服务的生活类软件主要提供的产品有水产海鲜,水果,蔬菜,食品,日常用品等.某机构为调查顾客对该软件的使用情况,在某地区随机访问了100人,访问结果如下表所示.使用人数
未使用人数
女性顾客
40
20
男性顾客
20
20
(1)、从被访问的100人中随机抽取2名,求所抽取的都是女性顾客且使用该软件的概率;(2)、用随机抽样的方法从该地区抽取10名市民,这10名市民中使用该软件的人数记为 , 问为何值时,的值最大?