广东省佛山市顺德区2023届高三下学期5月数学模拟仿真试卷
试卷更新日期:2023-06-02 类型:高考模拟
一、单项选择题:本题共8小题,每小题5分,共40分.
-
1. 已知集合 , 则( )A、 B、 C、 D、2. ( )A、 B、1 C、 D、-13. 从中随机取2个不同的数,则这2个数之和是4与6的公倍数的概率是( )A、 B、 C、 D、4. 如图,某圆柱体的高为是该圆柱体的轴截面.已知从点出发沿着圆柱体的侧面到点的路径中,最短路径的长度为 , 则该圆柱体的体积是( )
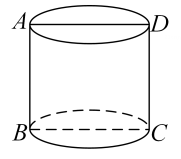 A、3 B、 C、 D、5. 已知的图象如图,则的解析式可能是( )
A、3 B、 C、 D、5. 已知的图象如图,则的解析式可能是( ) A、 B、 C、 D、6. 已知 , 若动点满足 , 则的最大值是( )A、18 B、9 C、3 D、7. 已知椭圆的下焦点为 , 右顶点为 , 直线交椭圆于另一点 , 且 , 则椭圆的离心率是( )A、 B、 C、 D、8. 已知是函数的导函数,对于任意的都有 , 且 , 则不等式的解集是( )A、 B、 C、 D、
A、 B、 C、 D、6. 已知 , 若动点满足 , 则的最大值是( )A、18 B、9 C、3 D、7. 已知椭圆的下焦点为 , 右顶点为 , 直线交椭圆于另一点 , 且 , 则椭圆的离心率是( )A、 B、 C、 D、8. 已知是函数的导函数,对于任意的都有 , 且 , 则不等式的解集是( )A、 B、 C、 D、二、多项选择题:本题共4小题,每小题5分,共20分.
-
9. 的展开式中只有第六项的二项式系数最大,且常数项是-252,则下列说法正确的是( )A、 B、各项的二项式系数之和为1024 C、 D、各项的系数之和为102410. 所有的有理数都可以写成两个整数的比,例如如何表示成两个整数的比值呢?代表了等比数列的无限项求和,可通过计算该数列的前项的和,再令获得答案.此时 , 当时, , 即可得.则下列说法正确的是( )A、 B、为无限循环小数 C、为有限小数 D、数列的无限项求和是有限小数11. 已知函数是的两个极值点,且 , 下列说法正确的是( )A、 B、在上的单调递增区间为 C、在上存在两个不相等的根 D、若在上恒成立,则实数的取值范围是12. 设函数有4个零点,分别为 , 则下列说法正确的是( )A、 B、 C、的取值与无关 D、的最小值为10
三、填空题:本大题共4小题,每小题5分,满分20分.其中第16题第一空2分,第二空3分.
-
13. 已知命题或 , 则.14. 某机器生产的产品质量误差是的第60个百分位数,则.
附:若 , 则 ,
15. 已知双曲线的左右焦点分别为 , 直线与双曲线的一条渐近线平行,过作 , 垂足为 , 则的面积为.16. 在三棱锥中,是边长为6的等边三角形, , 三棱锥体积的最大值是;当二面角为时,三棱锥外接球的表面积是.四、解答题:本大题共6小题,满分70分.
-
17. 在中,角的对边为 , 设的面积为.(1)、求角的大小;(2)、若 , 过的重心点的直线与边的交点分别为 , , 请计算的值.18. 已知数列的前项的和为 , 数列为单调递增的等比数列,且有.(1)、求数列的通项公式;(2)、设数列满足 , 设的前项的和为 , 求的值.19. 如图,在三棱锥中, , 设点为上的动点.
 (1)、求面积的最小值;(2)、求平面与平面的夹角的余弦值.20. 篮球职业联赛通常分为常规赛和季后赛两个阶段.常规赛采用循环赛,胜率高或者积分高的球队进入季后赛,季后赛是淘汰赛,采用三局两胜制进行淘汰,最终决出总冠军.三局两胜制是指当比赛一方先赢得两局比赛时该方获胜,比赛结束.
(1)、求面积的最小值;(2)、求平面与平面的夹角的余弦值.20. 篮球职业联赛通常分为常规赛和季后赛两个阶段.常规赛采用循环赛,胜率高或者积分高的球队进入季后赛,季后赛是淘汰赛,采用三局两胜制进行淘汰,最终决出总冠军.三局两胜制是指当比赛一方先赢得两局比赛时该方获胜,比赛结束.附:
0.100
0.050
0.010
2.706
3.841
6.635
(1)、下表是甲队在常规赛80场比赛中的比赛结果记录表,由表中信息,依据的独立性检验,分析“主场”是否会增加胜率(计算结果保留两位小数).月份
比赛次数
主场次数
获胜次数
主场获胜次数
10月
8
3
6
3
11月
15
10
8
8
12月
14
7
8
5
1月
13
4
11
3
2月
11
7
6
5
3月
14
6
7
3
4月
5
3
4
3
(2)、甲队和乙队在季后赛中相遇,经过统计甲队在主场获胜的概率为 , 客场获胜的概率为.每场比赛场地为上一场比赛的获胜方的场地.(i)若第一场比赛在甲队的主场进行,设整个比赛的进行的局数为 , 求的分布列及数学期望;
(ii)设选择第一场为甲队的主场的概率为 , 问当为何值时,无论第一场比赛的场地在哪里,甲队最终获胜的概率相同,并求出此时甲队获胜的概率.