四川省绵阳市2023年中考三模数学试题

试卷更新日期：2023-06-01 类型：中考模拟

进入出卷网下载

一、选择题：本大题共12个小题，每小题3分，共36分．

1. 计算：（-2023）⁰=（）

A、 $- 2023$ B、 $- 1$ C、1 D、2023

查看试题解析
2. 从人社部获悉：今年年初全国各地进一步拓宽就业渠道，岗位送到家门口．截至3月8日，累计举办各类招聘活动5.1万场，发布岗位3300万个．其中3300万用科学记数法表示为（）

A、 $0.33 \times 10^{7}$ B、 $3.3 \times 10^{6}$ C、 $3.3 \times 10^{7}$ D、 $33 \times 10^{6}$

查看试题解析
3. 关于x的代数式 $\frac{1}{\sqrt{1 - x}}$ 在实数范围内有意义，则x的取值范围为（）

A、 $x \leq 1$ B、 $x \geq 1$ C、 $x < 1$ D、 $x > 1$

查看试题解析
4. 如图，直线 $l_{1} ∥ l_{2}$ ， $∠ 1$ 与 $∠ B A C$ 互补， $∠ B A C = 70$ °，则 $∠ 2 =$ （）

A、30° B、40° C、45° D、50°

查看试题解析
5. 已知 $2^{a} = b$ ，则 $2^{a + 1} =$ （）

A、b B、1＋b C、2＋b D、2b

查看试题解析
6. 如图，在平面直角坐标系中，等边三角形ABO的顶点B的横坐标为 $2 \sqrt{3}$ ，则AB边中点的坐标为（）

A、 $(\sqrt{3} ， 2)$ B、 $(\sqrt{3} ， 3)$ C、 $(2 ， 2)$ D、 $(3 ， 3)$

查看试题解析
7. 若关于x的一元二次方程 $(k - 3) x^{2} + 6 x + k^{2} - k = 0$ 有一个根为－1，则k的值为（）

A、－3 B、3 C、 $\pm 3$ D、9

查看试题解析
8. 周末，青华到公园游玩，参加套环游戏，共进行四局，套中的次数分别为1，2，3，4若将这组数每一个加1，则对这一组新数据描述正确的是（）

A、平均值不变 B、方差不变 C、中位数不变 D、众数不变

查看试题解析
9. 图中的梯形ABCD是水坝的一个截面图，阴影部分是外坡面土方的部分．其中 $A D ∥ B C$ ， $∠ C = 9 0^{o}$ ， $∠ B = 45^{o}$ ， $∠ D E C = 60^{o}$ ， $A B = 10 \sqrt{6}$ m，AD＝5m，则坝底外坡面土方的水平宽度BE长为（）

A、 $10 \sqrt{3}$ m B、 $(10 \sqrt{3} - 5)$ m C、 $(10 \sqrt{3} + 5)$ m D、 $(5 \sqrt{3} + 5)$ m

查看试题解析
10. 新能源车的技术越来越成熟，而且更加环保节能．小松同学的爸爸准备换一台车，通过对比两台续航里程相同的燃油车和新能源车，发现燃油车的每千米行驶费用比新能源车多0.54元，已知燃油车的油箱容积为40升，燃油价格为9元/升，新能源车电池容量为60千瓦时，电价为0.6元/千瓦时，则小松爸爸选择的两台汽车的续航里程是（）

A、600km B、500km C、450km D、400km

查看试题解析
11. 如图，矩形ABCD的边AB在x轴的正半轴上，点B在点A的右边，点C，D在第一象限， $A (1 ， 0)$ ， $C (7 ， b)$ ，点P在CD边上运动，若b取某个确定的值时，使得 $△ P O B$ 是等腰三角形的点P有三个可能位置，则b的取值范围是（）

A、 $b > \sqrt{13}$ B、 $\sqrt{13} \leq b \leq 4 \sqrt{3}$ C、 $\sqrt{13} \leq b \leq \frac{7}{2} \sqrt{3}$ D、 $\sqrt{13} \leq b \leq 4 \sqrt{3}$ ，且 $b \neq \frac{7}{2} \sqrt{3}$

查看试题解析
12. 如图，在 $▱ A B C D$ 中，将 $△ A B C$ 绕着点A逆时针方向旋转到 $△ A E F$ 的位置，点E恰好落在边BC上，EF与CD交于点M，AB＝6，AD＝8，BE＝2，则CM的长为（）

A、2 B、3 C、 $\frac{5}{2}$ D、 $\frac{9}{4}$

查看试题解析

二、填空题：本大题共6个小题，每小题4分，共24分．

13. 因式分解： $m x^{2} - 4 m y^{2} =$ ．

查看试题解析
14. 如图，已知圆锥的底面圆半径为l，则该圆锥的俯视图的面积为．

查看试题解析
15. 若点 $A (1 ， m)$ 与点 $B (- 1 ， 1 - | x |)$ 关于原点O成中心对称，则m的最小值为．

查看试题解析
16. 不等式组 ${\begin{array}{l} 3 x + 2 > 7 ， \\ \frac{x - 1}{2} \leq 1 \end{array}$ 的所有整数解的和为．

查看试题解析
17. 现代互联网技术的广泛应用，催生了快递行业的高速发展，我市某家快递公司，今年1月份与3月份完成投送的快递件数分别为10万件和12.1万件．如果按此平均速度增长，该公司4月份投递的快递总件数将达到万件．

查看试题解析
18. 如图，在矩形ABCD中， $A B = 2 \sqrt{3}$ ， BC＝6，点E在BC上，且CE＝AE，将 $△ A B C$ 沿对角线AC翻折到 $△ A F C$ ，连接EF．则 $\sin ∠ C E F =$ ．

查看试题解析

三、解答题：本大题共7个小题，共90分．

19.

(1)、计算： $\tan 60^{°} \times {(- 2)}^{- 1} - (\sqrt{\frac{3}{4}} - \sqrt[3]{8}) + | - \frac{1}{2} \sqrt{12} |$ ；

(2)、化简求值： $(\frac{x + 2}{x^{2} - 2 x} - \frac{x - 1}{x^{2} - 4 x + 4}) \div \frac{x - 4}{x}$ ，其中 $x = \sqrt{2} + 2$ ．

查看试题解析

20. 为更好地加强食品企业、学校的食品安全宣传工作，增强企业员工、全校师生对食品安全的防范意识，普及食品安全科学知识，食品安全委员会与市场监督管理局联合开展了线上知识竞赛活动．某校为了解学生对食品安全知识点掌握情况，对该校1500名学生同期开展了线下答题．用简单随机抽样的方法，随机抽取若干名学生统计答题成绩，分别制成如下频数分布表和频数分布直方图：

成绩（分)	须数	频率
50≤x<60	4	0.02
60≤x<70	16	a
70≤x<80	60	0.3
80≤x<90	b	0.45
90≤x<100	30	c

(1)、请填空：a＝ ▲ ， b＝▲ ， c＝▲ ，并补全频数分布直方图；

(2)、规定成绩70分以下（不含70分）的同学需继续参加线上食品安全知识学习，则估计该校需要继续参加线上学习的同学共有多少人？

(3)、现有3名男生2名女生共5位同学符合食品安全志愿者推荐要求，学校共有2个推荐名额，求从这5名同学中被推荐的2人性别相同的概率．

查看试题解析

21. 为迎接“三·八妇女节”购物高峰，某化妆品牌专卖店准备购进甲、乙两种化妆品．其中甲、乙两种化妆品的进价和售价如下表：

种类

甲

乙

进价（元/件）

m

n

售价（元/件）

250

200

购进3件甲种化妆品，4件乙种化妆品，共需620元；购进5件甲种化妆品，3件乙种化妆品，共需740元．

(1)、求m，n的值；

(2)、要使购进的甲、乙两种化妆品共200件的总成本不超过18100元，全部售出后的总利润不少于27000元，该专卖店应该如何进货才能获得最大利润？并求最大利润．

查看试题解析
22. 如图，在 $▱ A B C D$ 中，点E在CD上，连接BE，并延长BE至点F，连接CF，DF，BC＝CF， $∠ A B F = ∠ D F B$ ，连接BD交AE于点G，若AG＝DF．

(1)、求证： $△ A D E$ $≌$ $△ C F D$ ；

(2)、求证：CG垂直平分线段BF．

查看试题解析
23. 如图，在平面直角坐标系 $x O y$ 中，一次函数 $y = - \frac{1}{2} x + m$ （m为常数，且 $m > 0$ ）的图象交x轴于点A，交y轴于点B，点C在x轴上， $O C = \frac{m}{2}$ ，点D在反比例函数 $y = - \frac{6 m}{x} (x > 0)$ 的图象上， $D E ⊥ O A$ ，垂足为点E，四边形ABCD是矩形．

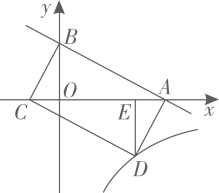(1)、用m表示点A，B的坐标，并求反比例函数的解析式；

(2)、已知点P在x轴上，且 $△ B D P$ 的面积等于40，求点P的坐标．

查看试题解析
24. 如图，AB是 $⊙ O$ 的直径，PA，PC是 $⊙ O$ 的两条切线，点A，C为切点，延长PC，AB相交于点D，若BD＝1，CD＝3，点F为弧AB的中点，连接AC．

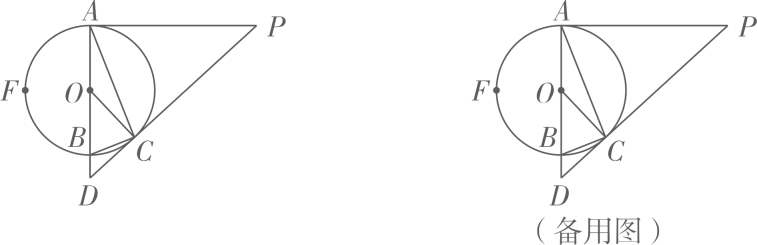(1)、连接OP交AC于点M，求证： $∠ A C B = ∠ A M O$ ；

(2)、设 $∠ O C B = α$ ，求 $\tan α$ 的值；

(3)、若点G与点F关于圆心O对称，连接CG，求CG的长．

查看试题解析
25. 如图，在平面直角坐标系 $x O y$ 中，菱形OABC的边OC在x轴上，点C在点O的右侧，抛物线的图像经过O，A，B三点， $∠ A O C = 60^{o}$ ， OA＝4，若点D以每秒2个单位的速度从点O出发沿边OA向点A运动，同时点E以每秒3个单位的速度从点O出发沿边OC向点C运动，点F在AC上， $∠ D E F = 60^{o}$ ，设运动时间为t．

(1)、求抛物线解析式；

(2)、设 $△ O D E$ 和 $△ C E F$ 的面积和为是S，当t为何值时，S最小，并求出S的最小值；

(3)、若点P在抛物线上，当t＝l时，在平面内是否存在点Q，使得以DE为边，点D，E，P，Q为顶点的四边形为矩形，若存在，求出点Q的横坐标；若不存在，请说明理由．

查看试题解析

种类	甲	乙
进价（元/件）	m	n
售价（元/件）	250	200