浙江省杭州市钱江教育共同体2023年中考数学模拟试卷（4月份）

试卷更新日期：2023-06-01 类型：中考模拟

进入出卷网下载

一、选择题（本大题共10小题，共30.0分。）

1. $- \frac{1}{2023}$ 的相反数是（）

A、2023 B、 $\frac{1}{2023}$ C、 $\pm \frac{1}{2023}$ D、-2023

查看试题解析
2. 下列运算一定正确的是（）.

A、 $2 a + 2 a = 2 a^{2}$ B、 $a^{2} \cdot a^{3} = a^{6}$ C、 ${(2 a^{2})}^{3} = 6 a^{6}$ D、 $(a + b) (a - b) = a^{2} - b^{2}$

查看试题解析
3. 费尔兹奖是国际上享有崇高声誉的一个数学奖项，每四年评选一次，主要授予年轻的数学家．下面的数据是部分获奖者获奖时的年龄 $($ 单位：岁 $)$ ：29，32，33，35，35，40，则这组数据的众数和中位数分别是（）

A、35，35 B、34，33 C、34，35 D、35，34

查看试题解析
4. 数学是研究化学的重要工具，数学知识广泛应用于化学邻域，比如在学习化学的醇类化学式中，甲醇化学式为 ${CH}_{3} OH$ ，乙醇化学式为 $C_{2} H_{5} OH$ ，丙醇化学式为 $C_{3} H_{7} OH \dots$ ，设碳原子的数目为 $n (n$ 为正整数 $)$ ，则醇类的化学式可以用下列哪个式子来表示（）

A、 $C_{n} H_{3 n} OH$ B、 $C_{n} H_{2 n - 1} OH$ C、 $C_{n} H_{2 n + 1} OH$ D、 $C_{n} H_{2 n} OH$

查看试题解析
5. 如图，直线 $a / / b$ ，直线 $c$ 分别交直线 $a$ ， $b$ 于点 $A$ ， $C$ ，点 $B$ 在直线 $b$ 上， $AB ⊥ AC$ ，若 $∠ 1 = 130 °$ ，则 $∠ 2$ 的度数是（）

A、 $30 °$ B、 $40 °$ C、 $50 °$ D、 $70 °$

查看试题解析
6. 若 $x + 2022 > y + 2023$ ，则下列不等式一定成立的是（）

A、 $3 x < 3 y$ B、 $1 + x < 1 + y$ C、 $- 2 x < - 2 y$ D、 $5 - x > 5 - y$

查看试题解析
7. 如图，已知 $AB$ 是 $⊙ O$ 的直径，弦 $CD ⊥ AB$ ，垂足为 $E$ ，且 $∠ ACD = 22.5 °$ ， $CD = 4$ ，则 $⊙ O$ 的半径长为（）

A、2 B、 $2 \sqrt{2}$ C、4 D、 $4 \sqrt{2}$

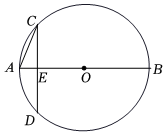查看试题解析
8. $《$ 九章算术 $》$ 中记载“今有共买羊，人出五，不足四十五；人出七，余三，问人数、羊价各几何？”其大意是：今有人合伙买羊，若每人出5钱，还差45钱；若每人出7钱，多余3钱，问合伙人数、羊价各是多少？若设人数为 $x$ 人，羊价 $y$ 钱，则下面所列方程组正确的是（）

A、 ${\begin{array}{l} 5 x = y - 45 \\ 7 x = y + 3 \end{array}$ B、 ${\begin{array}{l} 5 x = y - 45 \\ 7 x = y - 3 \end{array}$ C、 ${\begin{array}{l} x - 45 = \frac{y}{5} \\ x - 3 = \frac{y}{7} \end{array}$ D、 ${\begin{array}{l} \frac{x}{5} + 45 = y \\ \frac{x}{7} + 3 = y \end{array}$

查看试题解析
9. 四个全等的直角三角形按图示方式围成正方形 $ABCD$ ，过各较长直角边的中点作垂线，围成面积为 $S$ 的小正方形 $FGHI .$ 已知 $AE$ 为 $Rt △ ABE$ 较长直角边，若 $AE = 2 \sqrt{2} FG$ ，则正方形 $ABCD$ 的面积为（）

A、 $12 S$ B、 $10 S$ C、 $9 S$ D、 $8 S$

查看试题解析
10. 已知抛物线 $y = {ax}^{2} + bx + c (b > a > 0)$ 与 $x$ 轴最多有一个交点，现有以下三个结论：
$①$ 该抛物线的对称轴在 $y$ 轴左侧； $②$ 关于 $x$ 的方程 ${ax}^{2} + bx + c + 2 = 0$ 无实数根； $③ \frac{a + b + c}{3 a + 2 b}$ 的最小值为 $\frac{1}{3}$ ．其中，正确结论为（）

A、 $① ②$ B、 $② ③$ C、 $① ③$ D、 $① ② ③$

查看试题解析

二、填空题（本大题共6小题，共24.0分）

11. 分解因式： $2 x^{2} - 2 y^{2}$ = .

查看试题解析
12. 在一个盒子中装有若干乒乓球，小明为了探究盒子中所装乒乓球的数量，他先从盒子中取出一些乒乓球，记录了所取乒乓球的数量为 $m$ 个，并在这些乒乓球上做了记号“ $*$ ”，然后将它们放回盒子中，充分摇匀；接下来，他又从这个盒子中再次取出一些乒乓球，记录了所取乒乓球的数量为 $n$ 个，其中带有记号“ $*$ ”的乒乓球有 $p$ 个，小明根据实验所得的数据 $m = 20$ ， $n = 10$ ， $p = 2$ ，可估计出盒子中乒乓球的数量有个 $.$

查看试题解析
13. 将一个正八边形与一个正六边形如图放置，顶点 $A$ 、 $B$ 、 $C$ 、 $D$ 四点共线， $E$ 为公共顶点 $.$ 则 $∠ FEG =$ ．

查看试题解析
14. 已知反比例函数的表达式为 $y = \frac{1 + m}{x}$ ， $A (x_{1} ， y_{1})$ 和 $B (x_{2} ， y_{2})$ 是反比例函数图象上两点，若 $x_{1} < 0 < x_{2}$ 时， $y_{1} < y_{2}$ ，则 $m$ 的取值范围是．

查看试题解析
15. 如图，以边长为2的等边 $△ A B C$ 顶点A为圆心、一定的长为半径画弧，恰好与 $B C$ 边相切，分别交 $A B ， A C$ 于D，E，则图中阴影部分的面积是．

查看试题解析
16. 如图所示，长宽比为3：2的矩形 $ABCD$ ，将矩形 $ABCD$ 沿着 $EF$ 折叠，使点 $C$ 落到宽 $AD$ 的中点 $C'$ ，点 $B$ 落到点 $B'$ 处，则 $tan ∠ EFC =$ ．

查看试题解析

三、解答题（本大题共7小题，共66.0分。）

17.

(1)、计算： $cos 30 ° + | \sqrt{3} - 1 | + 3^{- 1} + {(\frac{1}{2})}^{0}$ ；

(2)、解不等式： $\frac{2 x - 1}{3} > \frac{3 x - 2}{2} - 1$ ．

查看试题解析
18. 第19届亚运会将于2023年9月23日至10月8日在杭州举行，杭州亚运会吉祥物是“宸宸”、“琮琮”和“莲莲”.将三张正面分别印有以上3个吉祥物图案的卡片（卡片的形状、大小、质地都相同）背面朝上、洗匀.

(1)、若从中任意抽取1张，抽得卡片上的图案恰好为“莲莲”的概率是.

(2)、若先从中任意抽取1张，记录后放回，洗匀，再从中任意抽取1张，求两次抽取的卡片图案不同的概率.（请用树状图或列表的方法求解）

查看试题解析
19. 如图所示，延长平行四边形 $ABCD$ 一边 $BC$ 至点 $F$ ，连结 $AF$ 交 $CD$ 于点 $E$ ，若 $\frac{DE}{CE} = \frac{1}{3}$ ．

(1)、若 $BC = 3$ ，求线段 $CF$ 的长；

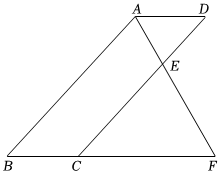(2)、若 $△ ADE$ 的面积为1，求平行四边形 $ABCD$ 的面积．

查看试题解析
20. 已知：一次函数 $y = 3 x - 2$ 的图象与某反比例函数的图象的一个公共点的横坐标为1.

(1)、求该反比例函数的解析式；

(2)、将一次函数 $y = 3 x - 2$ 的图象向上平移4个单位，求平移后的图象与反比例函数图象的交点坐标.

查看试题解析
21. 如图所示正方形 $ABCD$ 与等边 $△ ABE$ ，连结 $CE$ ，过点 $A$ 作 $CE$ 的垂线段 $AF$ ，连结 $FD$ ， $AC$ ．

(1)、求 $∠ FEA$ 的度数；

(2)、证明： $CE = \sqrt{2} FD$ ．

查看试题解析
22. 在平面直角坐标系 $xOy$ 中，抛物线 $y = (x - a - 1) (x + a - 1) + a$ ．

(1)、当 $a = 1$ 时，求抛物线与 $x$ 轴交点坐标；

(2)、求抛物线的对称轴，以及顶点纵坐标的最大值；

(3)、抛物线上两点 $A (x_{1} ， y_{1})$ 和 $B (x_{2} ， y_{2})$ ，当 $m < x_{1} < m + 1$ ， $m + 2 < x_{2} < m + 3$ 时，若存在 $y_{1} = y_{2}$ ，直接写出 $m$ 的取值范围．

查看试题解析
23. 已知点 $C$ 是以 $AB$ 为直径的圆上一点，连结 $AC$ ，在 $AB$ 上截取 $AD = AC$ ，连结 $CD$ 并延长交圆于点 $E$ ，连结 $AE$ ，设 $AC = kAB$ ．

(1)、如图1，若 $∠ EAB = 25 °$ 时，求 $∠ BAC$ 度数；

(2)、如图2，过点 $A$ 作 $AF ⊥ CD$ ，证明： $\frac{CD}{ED} = 2 k$ ；

(3)、如图3，若 $\frac{1}{2} < k < 1$ ，连结 $EB$ 并延长，交 $AC$ 的延长线于点 $F$ ，设 $△ BCF$ 的面积为 $S_{1}$ ，设 $△ AEF$ 面积为 $S_{2}$ ，用含 $k$ 的代数式表示 $S_{1}$ ： $S_{2}$ ．

查看试题解析