湖北省襄阳市宜城市2023年中考适应性考试数学试题

试卷更新日期：2023-06-01 类型：中考模拟

进入出卷网下载

一、选择题:(本大题共10个小题，每小题3分，共30分.)

1. －3的绝对值的相反数是（）

A、3 B、 $\frac{1}{3}$ C、－3 D、 $- \frac{1}{3}$

查看试题解析
2. 下列图形：等边三角形，等腰梯形，正方形，圆中，既是轴对称图形又是中心对称图形的有（）

A、1个 B、2个 C、3个 D、4个

查看试题解析
3. 下列计算正确的是（）

A、 $b^{3} \cdot b^{3} = 2 b^{3}$ B、 ${(b^{5})}^{2} = b^{7}$ C、 ${(- 2 b)}^{2} = - 4 b^{2}$ D、 ${(a b)}^{3} \div {(a b)}^{2} = a b$

查看试题解析
4. 如图的几何体的左视图是（）

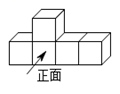A、 B、 C、 D、

查看试题解析
5. 已知反比例函数 $y = - \frac{6}{x}$ ，当1＜x＜3时，y的取值范围是（）

A、-2＜y＜0 B、-1＜y＜-3 C、2＜y＜6 D、-6＜y＜-2

查看试题解析
6. 下列事件中，是必然事件的是（）

A、任意画一个平行四边形，是中心对称图形 B、从0，1，2中任意抽取一个数字都是正数 C、抛掷1个骰子，掷得的结果不是1就是6 D、经过有交通信号灯的路口，遇到绿灯

查看试题解析
7. 如图，直线a∥b，∠1=39°，∠2=70°，则 $∠ A$ 度数是（）

A、39° B、21° C、31° D、70°

查看试题解析
8. 如图，在△ABC中，∠B＝30°，以点A为圆心的圆与边BC相切于点D，与AC，AB分别交于点E和点G，点F是优弧GE上一点，∠GFE＝50°，则∠CDE的度数是（）

A、10° B、20° C、30° D、40°

查看试题解析
9. 七巧板是一种古老的中国传统智力玩具，如图，在正方形纸板ABCD中，BD为对角线，E，F分别为BC，CD的中点， $A P ⊥ E F$ 分别交BD，EF于O，P两点，M，N分别为BO，DO的中点，连接MP，NF，沿图中实线剪开即可得到一副七巧板，则在剪开之前，关于该图形的下列说法：①图中的三角形都是等腰直角三角形；②图中的四边形MPEB是菱形；③四边形EFNB的面积占正方形ABCD面积的 $\frac{5}{8}$ ．正确的有（）

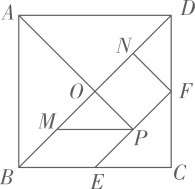A、①③ B、①② C、只有① D、②③

查看试题解析
10. 如图，二次函数y＝ax²＋bx＋c的图象经过点(1，0)，对称轴是直线x＝－1，下列结论：
①abc＞0，② b²－4ac≥0 ，③2a－b＝0，④3a＋2c＜0中错误的个数是（）

A、1 B、2 C、3 D、4

查看试题解析

二、填空题（本大题共6个小题，每小题3分，共18分）

11. 截至北京时间4月14日6时30分，全球累计确诊新冠肺炎病例超过435万例．用科学记数法表示435万是．

查看试题解析
12. 若式子 $\frac{\sqrt{2 x - 1}}{x - 1}$ 有意义，则 $x$ 的取值范围是．

查看试题解析
13. 一个不透明的袋子中装有红、白小球各两个，这些小球除颜色外无其他差别，从袋子中随机摸出一个小球后，放回并摇匀，再随机摸出一个小球，则两次摸出的小球是一红一白的概率为．

查看试题解析
14. 某学生推铅球，铅球所经过的路线是抛物线的一部分，若这名学生出手点A（0，1.6），铅球路线最高处为B（6，4），则该学生将铅球推出的距离是．

查看试题解析
15. 等腰三角形腰长为8，面积为16，则底角的度数为．

查看试题解析
16. 如图，矩形ABCD中，AB＝3，BC=4，E是BC中点，CD上有一动点M，连接EM、BM，将△BEM沿着BM翻折得到△BFM，连接DF，CF，则 $D F + \frac{1}{2} C F$ 的最小值为．

查看试题解析

三、解答题（本大题共9个小题，共72分．）

17. 先化简，再求值： $（ \frac{x^{2}}{x - 1} - x + 1) \div \frac{4 x^{2} - 4 x + 1}{x - 1}$ ，其中x= $\frac{\sqrt{2} + 1}{2}$ ．

查看试题解析
18. 某校根据课程设置要求，开设了数学类拓展性课程，为了解学生最喜欢的课程内容，随机抽取了部分学生进行问卷调查（每人必须且只选其中一项），并将统计结果绘制成如下统计图（不完整）．根据统计图提供的信息，解答下列问题：

(1)、m＝， n＝；

(2)、在扇形统计图中，“C．实验探究”所对应的扇形的圆心角度数是度；

(3)、请根据以上信息直接在答题卡上补全条形统计图；

(4)、该校共有1600名学生，试估计全校最喜欢“思想方法”的学生人数．

查看试题解析
19. 如图，小明想要利用无人机测量他家附近一座古塔（AB）的高度．在古塔所在的地平面上选定点C．在C处测得古塔顶端A点的仰角为53°，小明遥控无人机悬停在点C正上方的D处时，测得古塔顶端A点的俯角为26.6°，若观测点到古塔的水平距离（BC）为30m，求古塔（AB）的高度以及无人机离地面的高度（CD）．（参考数据：tan26.6°≈0.5，sin37°＝cos53°≈0.6，tan37°≈0.75）

查看试题解析
20. 如图，在矩形 $A B C D$ 中， $A B = 6 ， A D = 8$ ，

(1)、作∠BAC 的角平分线，交BC于点E；

(2)、求 $△ A E C$ 的周长．

查看试题解析
21. 已知关于x的一元二次方程x²－4x+m+1＝0有实数根．

(1)、求m的取值范围；

(2)、如果方程的两个实数根为x₁ ， x₂ ，且 $(x_{1} - 1) (x_{2} - 1) \geq - 1$ ，求m的所有整数值的和．

查看试题解析
22. 如图，PA是⊙O的切线，A是切点，AC是⊙O的直径，点B是⊙O的上一点，且OP∥BC，OP交⊙O于点D.

(1)、求证：PB是⊙O的切线；

(2)、若AC=OP=4，求阴影部分的面积.

查看试题解析
23. “五·一”前夕，某蛋糕店推出A、B两种不同口味的蛋糕.3个A种蛋糕和5个B种蛋糕的利润和为380元，5个A种蛋糕和3个B种蛋糕的利润和为420元．

(1)、求每个A种蛋糕和B种蛋糕的利润；

(2)、蛋糕店计划每天制作两种蛋糕共50个，设制作A种蛋糕x个，两种蛋糕全部卖完共获利y元．
①求y与x之间的函数关系式；

②若每天制作A种蛋糕的个数不少于30个，且不超过B种蛋糕个数的4倍，求每天全部卖完这两种蛋糕获得的最大利润；

(3)、在（2）的条件下，该蛋糕店对A种蛋糕以每个优惠a（5≤a≤15）元的价格进行“五·一”促销活动，B种蛋糕价格不变，且每天全部卖完这两种蛋糕所获得的最大利润不低于2240元，请求出a的取值范围．

查看试题解析
24. 已知菱形ABCD的边长为4．∠ADC=60°，等边△AEF两边分别交边DC，CB于点E，F．

(1)、特殊发现：如图1，若点E，F分别是边DC，CB的中点．求证：菱形ABCD对角线AC，BD的交点O即为等边△AEF的外心；

(2)、若点E，F始终分别在边DC，CB上移动，等边△AEF的外心为点P．
①猜想验证：如图2．猜想△AEF的外心P落在哪条直线上，并加以证明；

②学以致用：如图3，当△AEF的面积最小时，过点P任作一直线分别交边DA于点M，交边DC的延长线于点N，求 $\frac{1}{D M} + \frac{1}{D N}$ 的值．

查看试题解析
25. 如图，在平面直角坐标系中，直线y＝－x－2与x轴交于点A，与y轴交于点B，抛物线y＝－(x－m)²＋m²的顶点为P，过点P分别作x轴，y轴的垂线交AB于点M，Q，直线PM交x轴于点N．

(1)、若点P在y轴的左侧，且N为PM中点，求抛物线的解析式；

(2)、求线段PQ长的最小值，并求出当PQ的长度最小时点P的坐标；

(3)、若P，M，N三点中，任意两点都不重合，且PN＞MN，求m的取值范围．

查看试题解析