浙江省金华市2022-2023学年八年级下学期数学期中试卷

试卷更新日期：2023-06-01 类型：期中考试

进入出卷网下载

一、选择题（本题有10小题，每小题3分，共30分）

1. 要使二次根式 $\sqrt{x - 1}$ 有意义，则x的取值范围是（）

A、 $x \geq 1$ B、 $x > 1$ C、 $x \geq - 1$ D、 $x > - 1$

查看试题解析
2. 下列各式中，能与 $\sqrt{2}$ 合并的是（）

A、 $2 \sqrt{5}$ B、 $\sqrt{7}$ C、 $3 \sqrt{2}$ D、 $\sqrt{3}$

查看试题解析
3. 下列手机手势解锁图案中，既是中心对称图形又是轴对称图形的是（）

A、 B、 C、 D、

查看试题解析
4. 用配方法将方程 $x^{2} - 4 x - 1 = 0$ 变形为 ${(x - 2)}^{2} = m$ ，则m的值是（）

A、4 B、5 C、6 D、7

查看试题解析
5. 五边形的外角和为（）

A、180° B、360° C、540° D、720°

查看试题解析
6. 用反证法证明命题“若 $| a | < 3$ ，则 $a^{2} < 9$ ”时，应假设（）

A、 $a \geq 3$ B、 $a < 3$ C、 $a^{2} \geq 9$ D、 $a^{2} > 9$

查看试题解析
7. 下列条件不能够判定“平行四边形 $A B C D$ 是菱形”的是（）

A、 $A B = B C$ B、 $A C ⊥ B D$ C、 $A D = C D$ D、 $A C = B D$

查看试题解析
8. 小组合作学习是一种有效的学习方式，有甲、乙两位同学讨论他们七人小组的期中数学成绩．甲说：“我们组考110分的人最多．”乙说：“我们组成绩排在最中间的恰好也是110分．”甲、乙两位同学的话反映出的统计量分别是（）

A、众数和平均数 B、平均数和中位数 C、众数和中位数 D、众数和方差

查看试题解析
9. 南宋数学家杨辉在他的著作《杨辉算法》中提出这样一个数学问题：“直田积八百六十四步，只云长阔共六十步，问长多阔几何．”意思是：一块矩形地的面积为864平方步，已知长与宽的和为60步，问长比宽多几步？设矩形的长为x步，则可列出方程为（）

A、 $x (x - 60) = 864$ B、 $x (60 - x) = 864$ C、 $x (x - 30) = 864$ D、 $(x - 30) (x - 60) = 864$

查看试题解析
10. 如图，用直尺和圆规在矩形ABCD内进行构图：以A为圆心，AD长为半径作弧交BC于点E，连结AE，再以E为圆心，EC长为半径作弧交AE于点F，连结DF．下列结论不一定成立的是……（）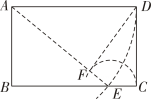

A、AE=BC B、DF⊥AE C、AB=DF D、AF=AB

查看试题解析

二、填空题（本题有6小题，每小题4分，共24分）

11. 一元二次方程 $2 x^{2} - 3 x + 1 = 0$ 的一次项系数为．

查看试题解析
12. 已知一组数据2，x，4的平均数为3，则x的值是．

查看试题解析
13. 小明设计了测量池塘两端AB距离的方案，如图，先取一点C，连结AC，BC，再取它们的中点D，E，测得DE=15米，则AB=米．

查看试题解析
14. 已知 $x = \sqrt{5} - 1$ ，则 $x^{2} + 2 x =$ ．

查看试题解析
15. 如图1，菱形纸片ABCD的边长为6cm，∠ABC＝60°，将菱形ABCD沿EF，GH折叠，使得点B，D两点重合于对角线BD上的点P（如图2）.若AE＝2BE，则六边形AEFCHG的面积为cm² ．

查看试题解析
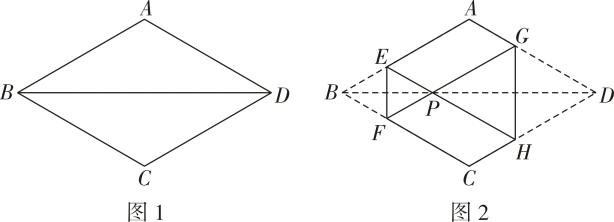16. 图1是四连杆开平窗铰链，其示意图如图2所示，MN为滑轨，AB、CE、PC、PD为固定长度的连杆.支点A固定在MN上，支点B固定在连杆CE上，支点D固定在连杆AB上.支点P可以在MN上滑动，点P的滑动带动点B、C、D、E的运动.已知MN=30cm，AM=1cm，AD=15cm，PC=BD=5cm，PD=BC=BE=9cm.窗户在关闭状态下，点B、C、D、E都在滑轨MN上.当窗户开到最大时，BC⊥MN.

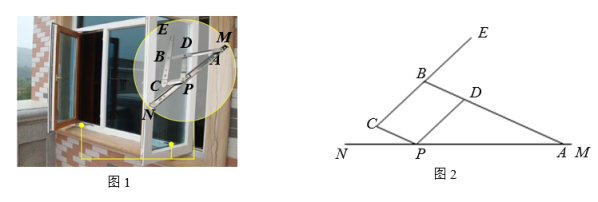(1)、若∠ABC=90°，则支点P与支点A的距离为cm；

(2)、窗户从关闭状态到开到最大的过程中，支点P移动的距离为cm.

查看试题解析

三、解答题（本题有8小题，共66分.）

17. 计算： $\sqrt{27} - \sqrt{12} + 6 \sqrt{\frac{1}{3}} - {(\sqrt{2})}^{2}$ .

查看试题解析
18. 解方程：x²＋2x－3＝0．

查看试题解析
19. 规定：每个顶点都在格点的四边形叫做格点四边形．在 $10 \times 6$ 的正方形网格中画出符合要求的格点四边形（每个小正方形的边长为1）．

(1)、在图1中画出一个以 $A B$ 为边的平行四边形．

(2)、在图2中画出一个以 $A B$ 为对角线的矩形，且它的周长为无理数．

查看试题解析

20. 为了解学生的科技知识情况，学校举行了“七、八年级学生科技知识竞赛”.七、八年级各有

300

名学生参加本次竞赛．现从两个年级各随机抽取

20

名学生的竞赛成绩（满分100分）进行分析，过程如下：

【收集数据】

七年级：94，87，86，85，83，81，80，80，79，79，77，76，75，75，75，75，73，71，70，59.

八年级：92，74，87，82，72，81，94，83 ，77，83，80，81，71，81，72，77，82，80，70，41.

【整理数据】

	40≤x≤49	50≤x≤59	60≤x≤69	70≤x≤79	80≤x≤89	90≤x≤100
七年级	0	1	0	11	7	1
八年级	1	0	0	7	a	2

【分析数据】

	平均数	众数	中位数
七年级	$78$	$75$	$b$
八年级	$78$	$81$	$80.5$

【应用数据】

(1)、由上表填空：

a =

，

b =

．

(2)、请估计该校七、八两个年级在本次竞赛中成绩在90分以上（含90分）的学生共有多少人？

查看试题解析

21. 如图，在 $▱$ ABCD中，对角线AC，BD相交于O，OE⊥AC交CD于点E．

(1)、求证：OA平分∠BAE.

(2)、若 $▱$ ABCD的周长为20，则△ADE的周长为．

查看试题解析
22. 已知关于x的方程 $x^{2} - (m + 1) x + 2 (m - 1) = 0$ ．

(1)、当方程一个根为x=3时，求m的值.

(2)、求证：无论m取何值，这个方程总有实数根.

(3)、若等腰△ABC的一腰长 $a = 6$ ，另两边b、c恰好是这个方程的两个根．则△ABC的面积为．

查看试题解析

23. 根据以下素材，探索完成任务．

如何设计实体店背景下的网上销售价格方案？
素材1	某公司在网上和实体店同时销售一种自主研发的小商品，成本价为40元/件．
素材2	该商品的网上销售价定为60元/件，平均每天销售量是200件，在实体店的销售价定为80元/件，平均每天销售量是100件.按公司规定，实体店的销售价保持不变，网上销售价可按实际情况进行适当调整，需确保网上销售价始终高于成本价.
素材3	据调查，网上销售价每降低1元，网上销售每天平均多售出20件，实体店的销售受网上影响，平均每天销售量减少2件．
问题解决
任务1	计算所获利润	当该商品网上销售价为50元/件时，求公司在网上销售该商品每天的毛利润与实体店销售该商品每天的毛利润各是多少元？
任务2	拟定价格方案	公司要求每天的总毛利润（（总毛利润=网上毛利润＋实体店毛利润）达到8160元，求每件商品的网上销售价是多少元？
任务3	探究最大利润	该商品的网上销售价每件▲ 元时，该公司每天销售这种小商品的总毛利润最大.

查看试题解析

24. 如图1，在Rt△ABC中，∠C=90°，∠B=30°，AC=12，点P，Q分别是CA，AB上的动点，P从C出发以每秒3个单位长度的速度向终点A运动，Q从A出发以每秒8个单位长度的速度向终点B运动，两点同时出发，当其中一点到达终点时整个运动结束，设运动时间为t秒．过点Q作QM⊥BC于点M．

(1)、AP= ， QM= ．（用含t的代数式表示）

(2)、如图2，已知点D为BC中点，连结QD，PD，以QD，PD为邻边作 $▱$ DPEQ．
①当PA=3PC时，求QD的长；

②在运动过程中，是否存在某一时刻，使得 $▱$ DPEQ的一边落在Rt△ABC的某边上？若存在，求出所有符合条件的t的值；若不存在，请说明理由.

查看试题解析