湖北省黄冈市教改联盟2023年中考第二次模拟考试数学试卷

试卷更新日期：2023-06-01 类型：中考模拟

进入出卷网下载

一、选择题（共8小题,每小题3分，共24分）

1. - $\frac{1}{2023}$ 的绝对值是（）

A、 $\frac{1}{2023}$ B、- $\frac{1}{2023}$ C、-2023 D、2023

查看试题解析
2. 中华人民共和国第十四届人民代表大会第一次会议政府工作报告指出：2023年国内生产总值预期增长目标5%左右，城镇新增就业1200万人左右，将1200万用科学记数法表示为（）

A、 $12 \times 1 0^{6}$ B、 $1.2 \times 1 0^{7}$ C、 $1.2 \times 1 0^{8}$ D、 $0.12 \times 1 0^{8}$

查看试题解析
3. 如图，a∥b，点B在直线b上，且AB⊥BC，∠1＝42°，那么∠2的度数为（）

A、42° B、45° C、48° D、52°

查看试题解析
4. 某正方体的每个面上都有一个汉字，如图是它的一种展开图，那么原正方体中，与“国”字所在面相对的面上的汉字是（）

A、全 B、面 C、依 D、法

查看试题解析
5. 已知点A（a-1，3）点B（-3，a+1），且直线AB∥y轴，则a的值为（）

A、1 B、-1 C、2 D、-2

查看试题解析
6. 如图，AB为⊙O的直径，弦CD交AB于点E， $\overset{⌢}{B C} = \overset{⌢}{B D}$ ， ∠CDB＝30°， $A C = 3 \sqrt{3}$ ，则OE的长为（）

A、 $\frac{\sqrt{3}}{2}$ B、 $\sqrt{3}$ C、 $\frac{3}{2}$ D、2

查看试题解析
7. 如图，在矩形ABCD中，连接BD，分别以B、D为圆心，大于 $\frac{1}{2}$ BD的长为半径画弧，两弧交于P、Q两点，作直线PQ，分别与AD、BC交于点M、N，连接BM、DN．若AD＝4，AB＝2．则四边形MBND的周长为（）

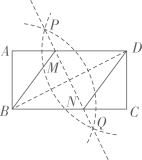A、 $\frac{5}{2}$ B、5 C、10 D、20

查看试题解析
8. 二次函数y＝ax²+bx+c（a≠0）的图象的一部分如图所示，已知图象经过点（-1，0），其对称轴为直线x＝1．下列结论：①abc＜0；②b²-4ac＞0；③8a+c＞0；④若抛物线经过点（-3，n），则关于x的一元二次方程ax²+bx+c＝n（a≠0）的两根分别为-3，5．其中正确的有（）

A、①②③ B、①②④ C、①③④ D、②③④

查看试题解析

二、填空题（共8小题，每小题3分，共24分）

9. 二次根式 $\frac{1}{\sqrt{x + 5}}$ 有意义，那么x的取值范围是．

查看试题解析
10. 分解因式：xy²﹣4x= ．

查看试题解析
11. 已知一组数据1，a，3，6，7，它的平均数是5，则这组数据的中位数是．

查看试题解析
12. 设x₁ ， x₂是一元二次方程x²-5x+4＝0的两个实数根，则 $\frac{1}{x_{1}} + \frac{1}{x_{2}}$ 的值为．

查看试题解析
13. 如图，将一个边长为20cm的正方形活动框架（边框粗细忽略不计）扭动成四边形ABCD．若∠BAD＝60°，则对角线AC＝cm．

查看试题解析
14. 如图，某数学兴趣小组测量一棵树CD的高度，在点A处测得树顶C的仰角为45°，在点B处测得树顶C的仰角为60°，且A，B，D三点在同一直线上，若AB＝20m，则这棵树CD的高度约为 m．（按四舍五入法将结果保留小数点后一位，参考数据： $\sqrt{3} \approx 1.732$ ）

查看试题解析
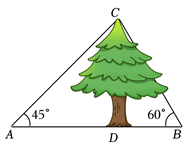15. 人们把 $\frac{\sqrt{5} - 1}{2}$ ≈0.618这个数叫做黄金比，著名数学家华罗庚优选法中的“0.618法”就应用了黄金比．设a＝ $\frac{\sqrt{5} - 1}{2} ， b = \frac{\sqrt{5} + 1}{2}$ ，记 $S_{1} = \frac{1}{1 + a} + \frac{1}{1 + b} ， S_{2} = \frac{2}{1 + a^{2}} + \frac{2}{1 + b^{2}}$
…，S₁₀₀＝ $\frac{100}{1 + a^{100}} + \frac{100}{1 + b^{100}}$ ，则S₁+S₂+…+S₁₀₀＝．

查看试题解析
16. 如图，将正方形ABCD放置在平面直角坐标系中，点B为坐标原点，点C（4，0），A分别在x轴、y轴上，点E是BC边上一动点，将线段AE绕点E顺时针旋转90°，得到线段EP ， Q是DE的中点，连接PQ，当PQ的长度取最小值时，BE的长度为.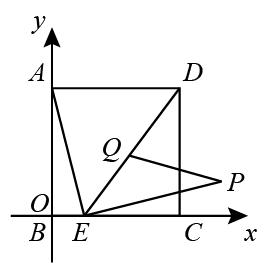

查看试题解析

三、解答题（共8小题，共72分）

17. 先化简，再求值： $(\frac{a + 1}{a - 1} + 1) \div \frac{2 a}{a^{2} - 1}$ ，其中a=2023．

查看试题解析
18. 某商场计划购进A、B两种新型台灯共80盏，它们的进价与售价如表所示：

类型价格

进价（元/盏）

售价（元/盏）

A型

30

45

B型

50

70

(1)、若商场预计进货款为2900元，则这两种台灯各购进多少盏？

(2)、将两种台灯全部售出，若总利润不低于1500元，则该商场最多购进多少盏A型台灯？

查看试题解析
19. 前两年，“碳中和，碳达峰”成为高频热词，为了解学生对“碳中和、碳达峰”知识的知晓情况，某校团委随机对该校九年级部分学生进行了问卷调查，调查结果共分成四个类别：A表示“从未听说过”，B表示“不太了解”，C表示“比较了解”，D表示“非常了解”．根据调查统计结果，绘制成两种不完整的统计图，请结合统计图，回答下列问题：

(1)、参加这次调查的学生总人数为▲ 人；将条形统计图补充完整；

(2)、扇形统计图中，B部分扇形所对应的圆心角是；

(3)、若该中学共有学生2000人，请根据上述调查结果，估计该中学学生中对“碳中和、碳达峰”知识达到“比较了解”和“非常了解”程度的总人数；

(4)、在D类的学生中，有2名男生和2名女生，现需从这4名学生中随机抽取2名“碳中和、碳达峰”知识的义务宣讲员，请利用画树状图或列表的方法，求所抽取的2名学生恰好是1名男生和1名女生的概率．

查看试题解析
20. 如图，AB是⊙O的直径，CD与⊙O相切于点C，与AB的延长线交于点D，DE⊥AD且与AC的延长线交于点E．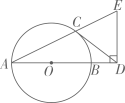

(1)、求证：△DCE是等腰三角形；

(2)、若tanA＝ $\frac{1}{2}$ ， AB＝3，求BD的长．

查看试题解析
21. 如图，直线y＝- $\frac{3}{2}$ x+b与反比例函数y＝ $\frac{12}{x}$ 的图象相交于点A，B，已知点A的纵坐标为6．

(1)、求b的值；

(2)、求B点坐标；

(3)、若点C是x轴上一点，且△ABC的面积为6，求点C的坐标．

查看试题解析
22. 某商品市场销售抢手，其进价为每件80元，售价为每件130元，每个月可卖出500件；据市场调查，若每件商品的售价每上涨1元，则每个月少卖2件（每件售价不能高于240元）．设每件商品的售价上涨x元（x为正整数），每个月的销售利润为y元．

(1)、求y与x的函数关系式，并直接写出自变量x的取值范围；

(2)、每件商品的涨价多少元时，每个月可获得最大利润？最大的月利润是多少元？

(3)、每件商品的涨价多少元时，每个月的利润恰为41800元？根据以上结论，请你直接写出x在什么范围时，每个月的利润不低于41800元？

查看试题解析
23. 如图①，在等边△ABC中，点D、E分别是AB、AC上的点，BD＝AE，BE与CD交于点O．

(1)、求∠BOC的度数；

(2)、如图②，以CO为边作等边△OCF，AF与BO相等吗？并说明理由；

(3)、如图③，在（2）的条件下，若点G是BC的中点，连接AO、GO，判断AO与GO有什么数量关系？并说明理由．

查看试题解析
24. 如图1，在平面直角坐标系中，抛物线y＝ax²+bx+4交x轴于A（-4，0）、B（2，0）两点，交y轴于点C，连接AC，直线AC解析式为y＝kx+m．

(1)、a=；b=；k=；m= ．

(2)、如图2．点P为线段AC上方的抛物线上一动点，点F为x轴上一个动点，连接PA、PC，当△PAC面积最大时，求 $PF + \frac{\sqrt{2}}{2} FB$ 的最小值，并求出此时P点的坐标．

(3)、在（2）的条件下，将抛物线向右移两个单位，再向上移两个单位，得到新抛物线，点E是新抛物线对称轴上一点，点N是新抛物线上一点，直接写出所有使得以点B、P、N、E为顶点的四边形是平行四边形的点N的坐标．

查看试题解析

类型价格	进价（元/盏）	售价（元/盏）
A型	30	45
B型	50	70