浙江省温州市洞头区洞头区2022-2023学年八年级下学期期中数学试题
试卷更新日期:2023-06-01 类型:期中考试
一、单选题
-
1. 在下列方程中,属于一元二次方程的是( )A、 B、 C、 D、2. 下列运算正确的是( )A、 B、 C、 D、3. 四名射击运动员(甲、乙、丙、丁)在一次连续10次的射击训练中的成绩如表:
甲
乙
丙
丁
平均环数
9.0
9.1
9.0
8.9
方差
2
3
1
4
则射击成绩发挥最稳定的是( )
A、甲 B、乙 C、丙 D、丁4. 如图,在平行四边形中, , 则的度数是( )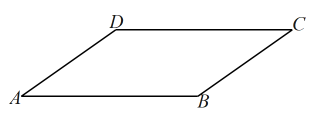 A、 B、 C、 D、5. 用配方法解一元二次方程 时,此方程可变形为( )A、 B、 C、 D、6. 用反证法证明命题:“在中,对边是 , 若 , 则”的第一步应假设( )A、 B、 C、 D、7. 关于 x 的一元二次方程有两个相等的实数根,则c的值是( )A、-36 B、-9 C、9 D、368. 在一次数学测验中,甲、乙、丙、丁四位同学的成绩分别是80、x、80、60,若这四位同学成绩的众数与平均数恰好相等,则他们成绩的中位数是( )A、60 B、70 C、80 D、1009.
A、 B、 C、 D、5. 用配方法解一元二次方程 时,此方程可变形为( )A、 B、 C、 D、6. 用反证法证明命题:“在中,对边是 , 若 , 则”的第一步应假设( )A、 B、 C、 D、7. 关于 x 的一元二次方程有两个相等的实数根,则c的值是( )A、-36 B、-9 C、9 D、368. 在一次数学测验中,甲、乙、丙、丁四位同学的成绩分别是80、x、80、60,若这四位同学成绩的众数与平均数恰好相等,则他们成绩的中位数是( )A、60 B、70 C、80 D、1009.如图,在▱ABCD中,∠DAB的平分线交CD于点E,交BC的延长线于点G,∠ABC的平分线交CD于点F,交AD的延长线于点H,AG与BH交于点O,连接BE,下列结论错误的是( )
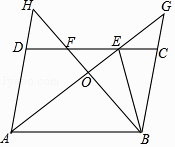 A、BO=OH B、DF=CE C、DH=CG D、AB=AE10. 如图,已知D、E分别为的边的中点,为的中线,连接 , 若四边形的面积为15,则的面积为( )
A、BO=OH B、DF=CE C、DH=CG D、AB=AE10. 如图,已知D、E分别为的边的中点,为的中线,连接 , 若四边形的面积为15,则的面积为( )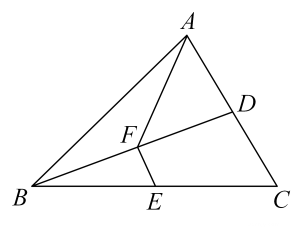 A、20 B、24 C、26 D、30
A、20 B、24 C、26 D、30二、填空题
-
11. 当时,二次根式的值是 .12. 方程 的根是.13. 若点与点关于原点成中心对称,则点的坐标是 .14. 若一个多边形的内角和是900º,则这个多边形是边形.15. 某校食堂有8元、10元、12元三种价格的饭菜供学生们选择(每人限购1份).三月份购买这三种价格饭菜的学生比例分别为30%,50%,20%,则该校三月份学生每餐购买饭菜的平均费用是元.16. 某经济开发区,今年一月份工业产值达亿元,二月、三月产值和为125亿元,二月、三月平均每月的增长率是多少?若设平均每月的增长率为 , 根据题意,可列方程为 .17. 如图,平行四边形中,点E在边上,以为折痕,将向上翻折,点A正好落在上的点F,若的周长为10,的周长为24,则的长为.
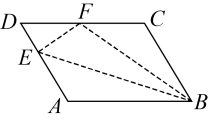 18. 如图,中, , , 四边形、四边形和四边形都是正方形,过点E作的平行线交于点P,连接则四边形的面积是;若四边形的面积是四边形的面积的5倍,则的值为.
18. 如图,中, , , 四边形、四边形和四边形都是正方形,过点E作的平行线交于点P,连接则四边形的面积是;若四边形的面积是四边形的面积的5倍,则的值为.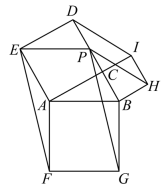
三、解答题
-
19.(1)、计算:;(2)、解方程: .20. 如图,按要求作格点四边形.
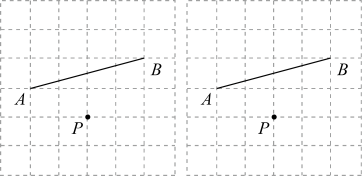 (1)、在图①中画出以为顶点的平行四边形,使点在该图形内部(不包括在边上).(2)、在图②中画出以为顶点的平行四边形,使该图形的一边所在直线与垂直.21. 【问题情境】数学活动课上,老师带领同学们开展“利用树叶的特征对树木进行分类”的实践活动.
(1)、在图①中画出以为顶点的平行四边形,使点在该图形内部(不包括在边上).(2)、在图②中画出以为顶点的平行四边形,使该图形的一边所在直线与垂直.21. 【问题情境】数学活动课上,老师带领同学们开展“利用树叶的特征对树木进行分类”的实践活动.
【实践发现】同学们随机收集芒果树、荔枝树的树叶各10片,通过测量得到这些树叶的长y
(单位:cm),宽x(单位:cm)的数据后,分别计算长宽比,整理数据如下:
1
2
3
4
5
6
7
8
9
10
芒果树叶的长宽比
3.8
3.7
3.5
3.4
3.8
4.0
3.6
4.0
3.6
4.0
荔枝树叶的长宽比
2.0
2.0
2.0
2.4
1.8
1.9
1.8
2.0
1.3
1.9
【实践探究】分析数据如下:
平均数
中位数
众数
方差
芒果树叶的长宽比
3.74
m
4.0
0.0424
荔枝树叶的长宽比
1.95
n
0.0669
【问题解决】
(1)、m= , n= ,求荔枝树叶的长宽比的平均数.(2)、A同学说:“从树叶的长宽比的方差来看,我认为芒果树叶的形状差别大.”B同学说:“从树叶的长宽比的平均数、中位数和众数来看,我发现荔枝树叶的长约为宽的两倍.” 以上两位同学的说法中,合理的是同学;(3)、现有一片长 , 宽的树叶,请判断这片树叶更可能来自于芒果、荔枝中的哪种树?并给出你的理由.22. 如图,在平行四边形中,E,F是直线上的两点, .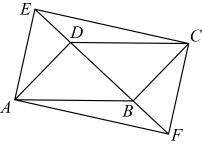 (1)、求证:四边形是平行四边形;(2)、若 , , , 且 , 求的长.23. 有一块长为米,宽为米的长方形场地,计划在该场地上修建宽均为x米的两条互相垂直的道路,余下的四块长方形场地建成草坪.
(1)、求证:四边形是平行四边形;(2)、若 , , , 且 , 求的长.23. 有一块长为米,宽为米的长方形场地,计划在该场地上修建宽均为x米的两条互相垂直的道路,余下的四块长方形场地建成草坪. (1)、已知 , , 且四块草坪的面积和为312平方米,则每条道路的宽为多少米?(2)、若 , , 且四块草坪的面积和为312平方米,则原来矩形场地的长和宽各为多少米?(3)、已知 , , 现要在场地上修建若干条宽均为2米的纵横小路,假设有条水平方向的小路,条竖直方向的小路(其中n为常数),使草坪地的总面积为平方米,则(直接写出答案).24. 如图,点O是坐标原点,四边形是平行四边形,点A的坐标为 , 点B的坐标为.动点P从O出发,沿射线方向以每秒2个单位的速度运动,点Q从B出发以每秒1个单位的速度向点C运动,它们同时出发,当点Q到达点C时P点也停止运动.设运动时间为t秒.
(1)、已知 , , 且四块草坪的面积和为312平方米,则每条道路的宽为多少米?(2)、若 , , 且四块草坪的面积和为312平方米,则原来矩形场地的长和宽各为多少米?(3)、已知 , , 现要在场地上修建若干条宽均为2米的纵横小路,假设有条水平方向的小路,条竖直方向的小路(其中n为常数),使草坪地的总面积为平方米,则(直接写出答案).24. 如图,点O是坐标原点,四边形是平行四边形,点A的坐标为 , 点B的坐标为.动点P从O出发,沿射线方向以每秒2个单位的速度运动,点Q从B出发以每秒1个单位的速度向点C运动,它们同时出发,当点Q到达点C时P点也停止运动.设运动时间为t秒.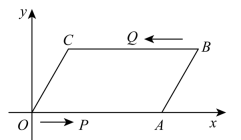 (1)、写出点C的坐标为;(2)、求当t为何值时,以P,Q,A,B为顶点的四边形是平行四边形;(3)、在点P,Q运动过程中,连接 ,
(1)、写出点C的坐标为;(2)、求当t为何值时,以P,Q,A,B为顶点的四边形是平行四边形;(3)、在点P,Q运动过程中,连接 ,①当t为何值时,使垂直于平行四边形的某一边.
②若点C关于的对称点恰好落在x轴上,则点Q的坐标为 ▲ .