浙江省绍兴市绍初教育集团2022-2023学年八年级下学期期中数学试题

试卷更新日期：2023-06-01 类型：期中考试

进入出卷网下载

一、单选题

1. 北京是全球首个既举办过夏季奥运会又举办过冬季奥运会的城市.下列各界冬奥会会徽部分图案中，既是轴对称图形，又是中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
2. 在▱ABCD中，∠A：∠B：∠C=1：2：1，则∠D等于（）

A、0° B、60° C、120° D、150°

查看试题解析
3. 若 $\sqrt{x + 1}$ 有意义，则字母x的取值范围是（）

A、 $x \geq - 1$ B、 $x > - 1$ C、 $x \geq$ 1 D、 $x > 1$

查看试题解析
4. 用配方法解方程： $x^{2} - 4 x + 2 = 0$ ，下列配方正确的是（）

A、 ${(x - 2)}^{2} = 2$ B、 ${(x + 2)}^{2} = 2$ C、 ${(x - 2)}^{2} = - 2$ D、 ${(x - 2)}^{2} = 6$

查看试题解析
5. 用反证法证明“ $a < b$ ”时应假设（）

A、 $a > b$ B、 $a \geq b$ C、 $a = b$ D、 $a \leq b$

查看试题解析
6. 在端午节到来之前，儿童福利院对全体小朋友爱吃哪几种粽子作调查，以决定最终买哪种粽子．下面的调查数据中最值得关注的是（）

A、方差 B、平均数 C、中位数 D、众数

查看试题解析
7. 一元二次方程 $x^{2} + 5 x + 1 = 0$ 根的情况是（）

A、有两个不相等的实数根 B、有两个相等的实数根 C、只有一个实数根 D、没有实数根

查看试题解析
8. 平行四边形的对角线分别为a和b ，一边长为14，则a和b的值可能是下面各组的数据中的（）

A、8和4 B、14和14 C、18和20 D、10和38

查看试题解析
9. 某经济开发区，今年一月份工业产值达50亿元，第一季度总产值为175亿元，二月、三月平均每月的增长率是多少？若设平均每月的增长率为 $x$ ，根据题意，可列方程为（）

A、 $50 (1 + x)^{2} = 175$ B、 $50 + 50 (1 + x) + 50 (1 + x)^{2} = 175$ C、 $50 (1 + x) + 50 (1 + x)^{2} = 175$ D、 $50 + 50 (1 + x)^{2} = 175$

查看试题解析
10. 如图，在四边形 $A B C D$ 中， $∠ A B C = 90 ° ， ∠ B A C = 30 °$ ， $B C = 2$ ， $E ， F$ 分别是 $A D ， C D$ 的中点，连接 $B E ， B F ， E F$ ，若四边形 $A B C D$ 的面积为 $6 \sqrt{3}$ ，则 $△ B E F$ 的面积为（）

A、 $\sqrt{3}$ B、 $2 \sqrt{3}$ C、 $\sqrt{3} + 2$ D、3

查看试题解析

二、填空题

11. 十边形的内角和是度．

查看试题解析
12. 已知一组数据为2、0、﹣1、3、﹣4，则这组数据的方差为．

查看试题解析
13. 已知三角形的三边长分别是4，5，6，则它的三条中位线围成的三角形的周长是．

查看试题解析
14. 若点 $P (a ， 2)$ 与 $Q (- 1 ， b)$ 关于原点对称，则 $\sqrt{2 a - 3 b} \div \sqrt{- \frac{a}{3 b}} =$ ．

查看试题解析
15. 已知三角形两边长分别是3和5，第三边的长为一元二次方程 $x^{2} - 7 x + 12 = 0$ 的一个根，则这个三角形的周长为．

查看试题解析
16. 下列给出的四个命题：
①若方程 $a x^{2} + b x + c = 0 (a \neq 0)$ 两根为－1和2，则 $2 a + c = 0$ ；

②若 $a^{2} - 5 a + 5 = 0$ ，则 $\sqrt{{(1 - a)}^{2}} = a - 1$ ；

③ $(a - 1) \sqrt{\frac{1}{1 - a}} = \sqrt{1 - a}$ ；

④若方程 $x^{2} + p x + q = 0$ 的两个实根中有且只有一个根为 $0$ ，那么 $p \neq 0$ ， $q = 0$ ．

其中是真命题的是．

查看试题解析

三、解答题

17. 计算：

(1)、 $- 3^{2} + \sqrt{3} \times \sqrt{6} - (\frac{1}{2})^{- 1}$

(2)、 $(2 - \sqrt{3}) (\sqrt{3} - 2) + \frac{1}{2 - \sqrt{3}} + (- 2023)^{0}$

查看试题解析
18. 解方程：

(1)、 $x^{2} - 8 x + 7 = 0$

(2)、 $(x + 1) (x - 1) = 2 \sqrt{2} x$

查看试题解析
19. 如图，在 $△ A B C$ 中， $A B = B C$ ， $B D$ 平分 $∠ A B C$ 交 $A C$ 于点D．点E为 $A B$ 的中点，连接 $D E$ ，过点E作 $E F ∥ B D$ 交 $C B$ 的延长线于点F．

(1)、求证：四边形 $D E F B$ 是平行四边形；

(2)、当 $A D = 12$ ， $B D = 5$ 时，则 $C F$ 的长为．

查看试题解析

20. 2023年大年初一上映两部电影，其一《满江红》以岳飞抗金为背景，讲述了南宋绍兴年间的历史事件，其二《流浪地球2》为观众展现末日危机下，人类在求生之路过程中的矛盾与冲突、勇气与团结．为了解学生对这两部影片的评价，某调查小组从该校九年级中随机抽取了20名学生对这两部作品分别进行打分（满分10分），并进行整理、描述和分析，下面给出了部分信息．《满江红》得分情况：7，8，7，10，7，6，9，9，10，10，8，9，8，6，6，10，9，7，9，9．

抽取的学生对两部作品分别打分的平均数，众数和中位数：

	平均数	众数	中位数
《满江红》	8.2	9	b
《流浪地球2》	7.8	c	8

根据以上信息，解答下列问题：

(1)、直接写出上述图表中的a，b，c的值；

(2)、根据上述数据，你认为该校九年级学生对哪部作品评价更高？请说明理由（写出一条理由即可）；

(3)、若该校九年级1100名学生都对这两部作品进行打分，你认为这两部作品一共可得到多少个满分？

查看试题解析

21. 在国家积极政策的鼓励下，中国新能源汽车的市场需求呈螺旋式上升，某汽车企业2020到2022这两年A型汽车年销售总量增加了69%，年销售单价下降了19%．

(1)、设2020年销售A型汽车总量为a万辆，销售单价为b万元，请用代数式填表：

年份	年销售A型汽车总量/万辆	年销售A型汽车单价/万元	年销售A型汽车总额/亿元
2020	a	b
2022	$1.69 a$	$0.81 b$

(2)、该汽车企业A型汽车这两年销售总额的年增长率相同，求年增长率．

查看试题解析

22. 已知有关于x的一元二次方程 $（ k + 1) x^{2} - (3 k + 1) x + 2 k = 0$ ．

(1)、求k的取值范围，并判断该一元二次方程根的情况；

(2)、若方程有一个根为-2，求k的值及方程的另一个根；

(3)、若方程的一个根是另一个根3倍，求k的值．

查看试题解析
23. 如图（1），在四边形 $A B C D$ 中， $A D$ $∥$ $B C$ ， $A D = 8 c m$ ， $B C = 12 c m$ ，有动点 $P$ 从 $A$ 点出发，在线段 $A D$ 上以 $1 c m / s$ 的速度向点 $D$ 运动，有动点 $Q$ 同时从 $C$ 点出发，在线段 $C B$ 上以 $2 c m / s$ 的速度向点 $B$ 运动，当其中一点到达时，另一点也随之停止运动．连接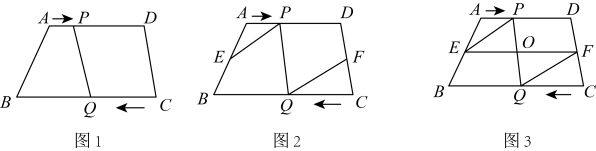 $P Q$ ，若运动时间是 $t$ 秒．

(1)、求当四边形 $A B Q P$ 和四边形 $P Q C D$ 其中一个是平行四边形时， $t$ 的取值；

(2)、如图（2），取 $A B$ 中点 $E$ ， $C D$ 中点 $F$ ，连接 $P E$ ， $Q F$ ，请求出使 $P E$ $∥$ $Q F$ 的时间 $t$ ；

(3)、在（2）中，继续连接 $E F$ ，与 $P Q$ 相交与点 $O$ ，如图（3）当 $P E$ $∥$ $Q F$ 时，请写出一个与EF有关的结论，并证明这个结论．

查看试题解析