浙江省金华市兰溪市兰溪八中2022-2023学年八年级下学期数学期中检测试题卷
试卷更新日期:2023-06-01 类型:期中考试
一、选择题(每小题3分,共30分)
-
1. 下列方程中,是一元二次方程的是( )A、3x+7=0 B、x2+5x=-6 C、x(x+5)=x3-1 D、3x2-=02. 要使式子无意义,则x的取值范围是( )A、x>2 B、x≤2 C、x≥2 D、x<23. 用配方法解方程x2-8x-7=0,则配方正确的是( )A、(x+4)2=23 B、(x-4)2=23 C、(x-4)2=9 D、(x-8)2=234. 能证明命题“x是实数,则(x-3)2>0”是假命题的反例是( )A、x=1 B、x=2 C、x=3 D、x=45. 既是轴对称图形又是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 6. 为了解某班学生双休户外活动情况,对部分学生参加户外活动的时间进行抽样调查,调查结果如下表:
6. 为了解某班学生双休户外活动情况,对部分学生参加户外活动的时间进行抽样调查,调查结果如下表:户外活动的时间(小时)
1
2
3
6
学生人数(人)
2
2
4
2
则关于“户外活动时间”这组数据的众数、平均数分别是( )
A、3,3 B、6,3 C、3,2 D、2,37. 将正六边形与正五边形按如图所示方式摆放,公共顶点为O,且正六边形的边AB与正五边形的边DE在同一条直线上,则∠COF的度数是( ) A、74° B、76° C、84° D、86°8. 如图,四边形ABCD为平行四边形,延长AD到E,使DE=AD,连结EB,EC,DB,添加一个条件,不能使四边形DBCE成为矩形的是( )
A、74° B、76° C、84° D、86°8. 如图,四边形ABCD为平行四边形,延长AD到E,使DE=AD,连结EB,EC,DB,添加一个条件,不能使四边形DBCE成为矩形的是( )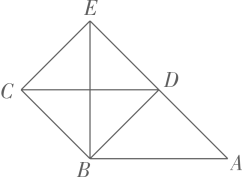 A、AB=BE B、CE⊥DE C、∠ADB=90° D、BE⊥AB9. 如图,△OAC和△BAD都是等腰直角三角形,∠ACO=∠ADB=90°,反比例函数y= 在第一象限的图象经过点B,若OA2-AB2=6,则k的值为( )
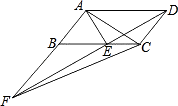
A、AB=BE B、CE⊥DE C、∠ADB=90° D、BE⊥AB9. 如图,△OAC和△BAD都是等腰直角三角形,∠ACO=∠ADB=90°,反比例函数y= 在第一象限的图象经过点B,若OA2-AB2=6,则k的值为( ) A、6 B、3 C、6 D、310. 如图,平行四边形ABCD中,AE平分∠BAD,交BC于点E,且AB=AE,延长AB与DE的延长线交于点F.下列结论中:
A、6 B、3 C、6 D、310. 如图,平行四边形ABCD中,AE平分∠BAD,交BC于点E,且AB=AE,延长AB与DE的延长线交于点F.下列结论中:①△ABC≌△EAD;
②△ABE是等边三角形;
③AD=AF;
④S△ABE=S△CDE;
⑤S△ABE=S△CEF .
其中正确的是( )
 A、①②③ B、①②④ C、①②⑤ D、①③④
A、①②③ B、①②④ C、①②⑤ D、①③④二、填空题(每小题4分,共24分)
-
11. 已知一个一元二次方程的一个根为2023,二次项系数是1,则这个一元二次方程可以是(只需写出一个方程即可).12. 如图,在平行四边形ABCD中,AB=5,AD=7,∠ABC的平分线交AD于点E,∠BCD的平分线交AD于点F,则线段EF的长为。
 13. 如图,已知矩形ABCD中,P、R分别是BC、DC上的点,E、F分别的是PA、PR的中点,如果DR=3,BC=4,则EF长为
13. 如图,已知矩形ABCD中,P、R分别是BC、DC上的点,E、F分别的是PA、PR的中点,如果DR=3,BC=4,则EF长为 14. 如果关于x的一元二次方程ax2+bx+c=0有两个实数根,且其中一个根为另一个根的2倍,则称这样的方程为“倍根方程”,以下关于倍根方程的说法,正确的是(写出正确说法的序号即可).
14. 如果关于x的一元二次方程ax2+bx+c=0有两个实数根,且其中一个根为另一个根的2倍,则称这样的方程为“倍根方程”,以下关于倍根方程的说法,正确的是(写出正确说法的序号即可).
①方程x2+2x-8=0是倍根方程;
②方程x2-3x+2=0是倍根方程;
③若(x-2)(mx+n)=0是倍根方程,则4m2+5mn+n2=0;
④若点(p,q)在反比例函数的图象上,则关于x方程px2+3x+q=0是倍根方程.15. 某同学用如图1中的一副七巧板拼成如图2的“帆船图”,已知正方形ABCD的边长为4,则图2中h的值为 . 16. 如图,在矩形ABCD中,AB=10cm,BC=4cm,M,N两点分别从A,B两点以2cm/s和1cm/s的速度在矩形ABCD边上沿逆时针方向运动,其中有一点运动到点D停止,当运动时间为秒时,△MBN为等腰三角形.
16. 如图,在矩形ABCD中,AB=10cm,BC=4cm,M,N两点分别从A,B两点以2cm/s和1cm/s的速度在矩形ABCD边上沿逆时针方向运动,其中有一点运动到点D停止,当运动时间为秒时,△MBN为等腰三角形.
三、解答题(共66分)
-
17. 计算:(1)、(2)、18. 解方程:(1)、 (x-5)2=8(x-5)(2)、 2x2-4x-3=0.19. 如图,点E是正方形外一点,且 . 请仅用无刻度的直尺按要求作图(保留作图痕迹).
 (1)、在图1中,作出BC边的中点M;(2)、在图2中,作出CD边的中点N.20. 田径队为从甲、乙两名运动员中选择一人参加比赛,对他们进行了6次百米测试,测试成绩如下表(单位:秒):
(1)、在图1中,作出BC边的中点M;(2)、在图2中,作出CD边的中点N.20. 田径队为从甲、乙两名运动员中选择一人参加比赛,对他们进行了6次百米测试,测试成绩如下表(单位:秒):第1次
第2次
第3次
第4次
第5次
第6次
平均成绩
中位数
甲
11.1
10.6
11.2
10.8
11.4
10.9
11.0
①
乙
10.5
10.0
11.0
11.0
10.5
10.0
②
10.5
(1)、完成表中填空:①;②(2)、平均测试成绩最好的是运动员。(填“甲”、“乙”)(3)、请计算甲6次测试成绩的方差;21. 如图,在正方形ABCD中,点E,F为对角线BD上两点,CE=CF. (1)、求证:AE=CE(2)、请你判断四边形AFCE的形状,(不必证明)(3)、若EF=6,DE=BF=3,求四边形AECF的周长.22. 兰溪联华超市今年三月初以每件40元的进价购进一批水磨年糕,当年糕售价为每件60元时,三月份共销售192件.四、五月该批年糕销售量持续走高,在售价不变的基础上,五月份的销售量达到300件.(1)、求四、五两个月销售量的月平均增长率;(2)、从六月份起,在五月份的基础上,联华超市决定采用降价促销的方式回馈顾客,经市场调查发现,该年糕每件降价2元,月销售量增加40件.在顾客获得最大实惠的前提下,当年糕每件降价多少元时,联华超市六月份仍可获利为6080元?23. 定义:把横、纵坐标均为整数的点称为整点。如图,反比例函数y= (×>0)与正比例函数y=×相交于整点A,与一次函数y=-x+t相交于整点B、C,正比例函数y=x与一次函数y=-x+t相交于点D,线段BC与线段AD上的整点个数之比记作m.
(1)、求证:AE=CE(2)、请你判断四边形AFCE的形状,(不必证明)(3)、若EF=6,DE=BF=3,求四边形AECF的周长.22. 兰溪联华超市今年三月初以每件40元的进价购进一批水磨年糕,当年糕售价为每件60元时,三月份共销售192件.四、五月该批年糕销售量持续走高,在售价不变的基础上,五月份的销售量达到300件.(1)、求四、五两个月销售量的月平均增长率;(2)、从六月份起,在五月份的基础上,联华超市决定采用降价促销的方式回馈顾客,经市场调查发现,该年糕每件降价2元,月销售量增加40件.在顾客获得最大实惠的前提下,当年糕每件降价多少元时,联华超市六月份仍可获利为6080元?23. 定义:把横、纵坐标均为整数的点称为整点。如图,反比例函数y= (×>0)与正比例函数y=×相交于整点A,与一次函数y=-x+t相交于整点B、C,正比例函数y=x与一次函数y=-x+t相交于点D,线段BC与线段AD上的整点个数之比记作m.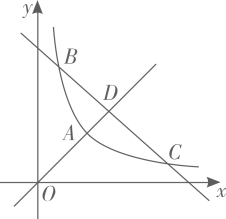 (1)、当k=4时,求D点的坐标和m值.(2)、当线段BC上的整点个数为7,AD=时,求t的值.(3)、当AD≤时,请直接写出t与m之间的关系式.24. 如图,在平面直角坐标系中,直线y=-x+5与反比例函数y=(×>0)的图象相交于点A(3,a)和点B(2,b),点D,C分别是×轴和y轴的正半轴上的动点,且满足CD∥AB.
(1)、当k=4时,求D点的坐标和m值.(2)、当线段BC上的整点个数为7,AD=时,求t的值.(3)、当AD≤时,请直接写出t与m之间的关系式.24. 如图,在平面直角坐标系中,直线y=-x+5与反比例函数y=(×>0)的图象相交于点A(3,a)和点B(2,b),点D,C分别是×轴和y轴的正半轴上的动点,且满足CD∥AB. (1)、求a,b的值及反比例函数的解析式;(2)、若OD=1,求点C的坐标,判断四边形ABCD的形状并说明理由;(3)、若点M是反比例函数y=(×>0)图象上的一个动点,当△AMD是以AM为直角边的等腰直角三角形时,求点M的坐标.
(1)、求a,b的值及反比例函数的解析式;(2)、若OD=1,求点C的坐标,判断四边形ABCD的形状并说明理由;(3)、若点M是反比例函数y=(×>0)图象上的一个动点,当△AMD是以AM为直角边的等腰直角三角形时,求点M的坐标.