广东省深圳市罗湖区2022-2023学年5月统考数学试卷
试卷更新日期:2023-06-01 类型:中考模拟
一、单选题(每小题3分,共30分)
-
1. 实数3的相反数是( )A、3 B、-3 C、 D、2. 下列立体图形中,俯视图与主视图不同的是( )A、
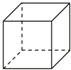 正方体
B、
正方体
B、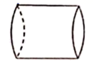 圆柱
C、
圆柱
C、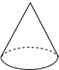 圆锥
D、
圆锥
D、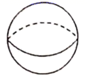 球
3. 为了解某地一天内的气温变化情况,比较适合使用的统计图是( )A、条形统计图 B、折线统计图 C、扇形统计图 D、频数直方图4. 港珠澳大桥是世界最长的跨海大桥,其中主体工程“海中桥隧”长达35.578公里,整个大桥造价超过720亿元人民币.数据“720亿”用科学记数法可表示为( )A、7.2×102 B、7.2×103 C、7.2×1010 D、7.2×10115. 下列运算正确的是( )A、(a-1)2=a2-1 B、(a2)2=a5 C、a3×a4=a7 D、a6÷a3=a26. 不等式组 的解集在数轴上表示正确的是( )A、
球
3. 为了解某地一天内的气温变化情况,比较适合使用的统计图是( )A、条形统计图 B、折线统计图 C、扇形统计图 D、频数直方图4. 港珠澳大桥是世界最长的跨海大桥,其中主体工程“海中桥隧”长达35.578公里,整个大桥造价超过720亿元人民币.数据“720亿”用科学记数法可表示为( )A、7.2×102 B、7.2×103 C、7.2×1010 D、7.2×10115. 下列运算正确的是( )A、(a-1)2=a2-1 B、(a2)2=a5 C、a3×a4=a7 D、a6÷a3=a26. 不等式组 的解集在数轴上表示正确的是( )A、 B、
B、 C、
C、 D、
D、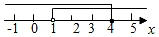 7. 小明在学习平行线的性质后,把含有60°角的直角三角板摆放在四边形ABCD上,如图,AD∥BC,若∠2=70°,则∠1=( )
7. 小明在学习平行线的性质后,把含有60°角的直角三角板摆放在四边形ABCD上,如图,AD∥BC,若∠2=70°,则∠1=( ) A、22° B、20° C、25° D、30°8. 下列事件中是不可能事件的是( )A、对角线相等且互相平分的四边形是矩形 B、平分弦的直径垂直于弦 C、将抛物线y=-2x2平移可以得到抛物线y=2x2+1 D、圆外一点引圆的两条切线,它们的切线长相等9. 我国古代《算法统宗》里有这样一首诗:“我问开店李三公,众客都来到店中,一房七客多七客,一房九客一房空.”诗中后两句的意思是:如果每一间客房住7人,那么有7人无房住;如果每一间客房住9人,那么就空出一间客房.设该店有客房x间、房客y人,下列方程组中正确的是( )
A、22° B、20° C、25° D、30°8. 下列事件中是不可能事件的是( )A、对角线相等且互相平分的四边形是矩形 B、平分弦的直径垂直于弦 C、将抛物线y=-2x2平移可以得到抛物线y=2x2+1 D、圆外一点引圆的两条切线,它们的切线长相等9. 我国古代《算法统宗》里有这样一首诗:“我问开店李三公,众客都来到店中,一房七客多七客,一房九客一房空.”诗中后两句的意思是:如果每一间客房住7人,那么有7人无房住;如果每一间客房住9人,那么就空出一间客房.设该店有客房x间、房客y人,下列方程组中正确的是( )
A、 B、 C、 D、10. 如图,为圆O的直径,C为圆O上一点,过点C作圆O的切线交的延长线于点D, , 连接 , 若 , 则的长度为( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题(每小题3分,共15分)
-
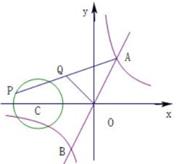
11. 因式分解:a2-9=.12. 习近平总书记在党的二十大报告中强调:“青年强,则国家强”.小明同学将“青”“年”“强”“则”“国”“家”“强”这7个字,分别书写在大小、形状完全相同的7张卡片上,搅匀后从中随机抽取一张,则这张卡片上恰好写着“强”字的概率是13. 已知α,β是方程x2-3x-4=0的两个实数根,则a2-3a+αβ的值为14. 如图,一次函数y=2x与反比例函数y= (k>0)的图象交于点A,B,点P在以C(-2,0)为圆心,1为半径的⊙C上,Q是AP的中点,若OQ长的最大值为 ,则k的值为。
 15. 如图,在锐角三角形ABC中,tanA= , BC= , 线段BD、CE分别是AC、AB边上的高线,连接DE,则三角形ADE面积的最大值是
15. 如图,在锐角三角形ABC中,tanA= , BC= , 线段BD、CE分别是AC、AB边上的高线,连接DE,则三角形ADE面积的最大值是
三、解答题(第16题5分,第17题7分,第18题8分,第19题8分,第20题8分,第21题9分,第22题10分)
-
16. 计算-12+|1-tan60°|-(3+)0+()-217. 先化简,再求值: , 其中a= , b=2.18. 某校500名学生参加植树活动,要求每人植4~7棵,活动结束后随机调查了部分学生每人的植树量,并分为四种类型,A:4棵,B:5棵,C:6棵,D:7棵.将各类的人数绘制成如下的扇形统计图和条形统计图.
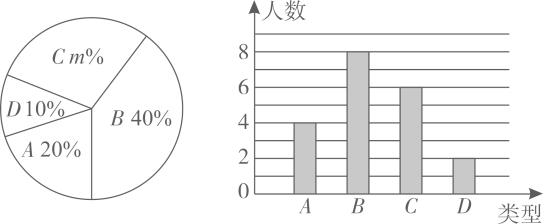 (1)、本次接受随机调查的学生人数为名,扇形统计图中m的值为;(2)、本次调查获取的样本数据的平均数为 , 众数为 , 中位数为;(3)、根据样本数据,估计这500名学生共植树多少棵.19. “双减”政策受到各地教育部门的积极响应,某校为增加学生的课外活动项目,现决定增购两种体育器材:跳绳和毽子.已知跳绳的单价比毽子的单价多3元,用800元购买的跳绳数量和用500元购买的毽子数量相同.(1)、求跳绳和毽子的单价分别是多少元?(2)、学校计划购买跳绳和毽子两种器材共600个,且要求跳绳的数量不少于毽子数量的3倍,跳绳的数量不多于452根,请问有几种购买方案并指出哪种方案学校花费最少.20. 在初中函数学习中,我们经历了列表、描点、连线画函数图象,结合图象研究函数性质并对其性质进行应用的过程.小丽同学学习二次函数后,对函数y=x2-2|x|(自变量x可以是任意实数)图象与性质进行了探究.请同学们阅读探究过程并解答:(1)、作图探究:
(1)、本次接受随机调查的学生人数为名,扇形统计图中m的值为;(2)、本次调查获取的样本数据的平均数为 , 众数为 , 中位数为;(3)、根据样本数据,估计这500名学生共植树多少棵.19. “双减”政策受到各地教育部门的积极响应,某校为增加学生的课外活动项目,现决定增购两种体育器材:跳绳和毽子.已知跳绳的单价比毽子的单价多3元,用800元购买的跳绳数量和用500元购买的毽子数量相同.(1)、求跳绳和毽子的单价分别是多少元?(2)、学校计划购买跳绳和毽子两种器材共600个,且要求跳绳的数量不少于毽子数量的3倍,跳绳的数量不多于452根,请问有几种购买方案并指出哪种方案学校花费最少.20. 在初中函数学习中,我们经历了列表、描点、连线画函数图象,结合图象研究函数性质并对其性质进行应用的过程.小丽同学学习二次函数后,对函数y=x2-2|x|(自变量x可以是任意实数)图象与性质进行了探究.请同学们阅读探究过程并解答:(1)、作图探究:①下表是y与x的几组对应值:
x
……
-4
-3
-2
-1
0
1
2
3
4
……
y
……
8
3
0
m
0
-1
0
n
8
……
m= ▲ , n= ▲
②在平面直角坐标系×Oy中,描出表中各组对应值为坐标的点,并根据描出的点,画出该函数的图象:
 (2)、深入思考:
(2)、深入思考:根据所作图象,回答下列问题:
①方程x2-2|x|= 0的解是;
②如果y=x2-2|x|的图象与直线y=k有4个交点,则k的取值范围是;
(3)、延伸思考:将函数y=x2-2|x|的图象经过怎样的平移可得到y1= (x+1)2- 2|x+1|-2的图象?请写出平移过程.
21. 如图1,已知:△ABC内接于圆O,AB=AC,连接AO并延长,交BC于点D. (1)、求证:AD⊥BC;(2)、如图2,过点B作BE⊥AC于点E,交圆O于点F,交AD于点G,连接AF、CF,求证:AG=AF;(3)、如图3,在(2) 的条件下,连接DE,CF=5,AF=3 , 求DE的长.22. 如图,矩形AOBC的顶点B,A分别在x轴,y轴上,点C坐标是(5,4),D为BC边上一点,将矩形沿AD折叠,点C落在x轴上的点E处,AD的延长线与x轴相交于点F.
(1)、求证:AD⊥BC;(2)、如图2,过点B作BE⊥AC于点E,交圆O于点F,交AD于点G,连接AF、CF,求证:AG=AF;(3)、如图3,在(2) 的条件下,连接DE,CF=5,AF=3 , 求DE的长.22. 如图,矩形AOBC的顶点B,A分别在x轴,y轴上,点C坐标是(5,4),D为BC边上一点,将矩形沿AD折叠,点C落在x轴上的点E处,AD的延长线与x轴相交于点F. (1)、如图1,求点D的坐标;(2)、如图2,若P是线段AF上一动点,PM⊥AC交AC于点M,PN⊥CF交CF于点N,设AP=t,FN=s,求s与t之间的函数关系式;(3)、在(2)的条件下,是否存在点P,使△PMN为等腰三角形?若存在,请直接写出点P的坐标;若不存在,请说明理由.
(1)、如图1,求点D的坐标;(2)、如图2,若P是线段AF上一动点,PM⊥AC交AC于点M,PN⊥CF交CF于点N,设AP=t,FN=s,求s与t之间的函数关系式;(3)、在(2)的条件下,是否存在点P,使△PMN为等腰三角形?若存在,请直接写出点P的坐标;若不存在,请说明理由.