浙江省宁波市2023年提前招生模拟考试数学试题

试卷更新日期：2023-06-01 类型：竞赛测试

进入出卷网下载

一、选择题（共10小题，每小题4分，共40分）

1. ﹣3的倒数为（）

A、﹣ $\frac{1}{3}$ B、 $\frac{1}{3}$ C、3 D、﹣3

查看试题解析
2. 下列计算正确的是（）

A、（x+y）²＝x²+y² B、x⁵•x＝x⁶ C、（xy²）³＝xy⁶ D、x²+x²＝2x⁴

查看试题解析
3. 研究表明，可燃冰是一种可替代石油的新型清洁能源，在我国某海域已探明的可燃冰储存量达150000000000立方米，其中数字150000000000用科学记数法可表示为（）

A、15×10¹⁰ B、0.15×10¹² C、1.5×10¹² D、1.5×10¹¹

查看试题解析
4. 如图是由6个大小相同的立方体组成的几何体，在这个几何体的三视图中，是中心对称图形的是（）

A、主视图 B、左视图 C、俯视图 D、主视图和左视图

查看试题解析
5. 如果将一组数据5、4、6、5、4、13、5依次重复写10次，会得到70个数组成的一组新数据，关于这组新数据的中位数、众数、平均数，下列说法正确的是（）

A、中位数和众数都是5 B、众数是10 C、中位数是4 D、中位数、平均数都是5

查看试题解析
6. 如图，在平行四边形ABCD中，以A为圆心，AB长为半径画弧交AD于F．分别以点F，B为圆心，大于 $\frac{1}{2}$ BF长为半径作弧，两弧交于点G，作射线AG交BC于点E，若BF＝6，AB＝5，则AE的长为（）

A、4 B、6 C、8 D、10

查看试题解析
7. 如图，Rt△ABC中，点D为斜边AB上一点，将△ACD沿着CD翻折至△ECD，恰有ED⊥BC，若AD＝2BD，则tan∠DCA的值为（）

A、2 B、 $\sqrt{5}$ C、 $\sqrt{6}$ D、3

查看试题解析
8. 我国古代著作《增删算法统宗》记载“绳索量竿”问题：“一条竿子一条索，索比竿子长一托．折回索子却量竿，却比竿子短一托．“其大意为：现有一根竿和一条绳索，用绳索去量竿，绳索比竿长5尺；如果将绳索对半折后再去量竿，就比竿短5尺．设绳索长x尺，竿长y尺，则符合题意的方程组是（）

A、 ${\begin{cases} x = y + 5 \\ \frac{1}{2} x = y - 5 \end{cases}$ B、 ${\begin{array}{l} x = y - 5 \\ \frac{1}{2} x = y + 5 \end{array}$ C、 ${\begin{array}{l} x = y + 5 \\ 2 x = y - 5 \end{array}$ D、 ${\begin{array}{l} x = y - 5 \\ 2 x = y + 5 \end{array}$

查看试题解析
9. 设二次函数y＝x²-kx+2k（k为实数）的图象过点（1，y₁），（2，y₂），（3，y₃），（4，y₄），设y₁-y₂＝a，y₃-y₄＝b，（）

A、若ab＜0，且a+b＜0，则k＜7 B、若ab＜0，且a+b＞0，则k＜5 C、若ab＞0，且a+b＜0，则k＞3 D、若ab＞0，且a+b＞0，则k＞7

查看试题解析
10. 如图，矩形ABCD中，E为边AD上一点（不为端点），EF⊥AD交AC于点F，要求△FBC的面积，只需知道下列哪个三角形的面积即可（）

A、△EBC B、△EBF C、△ECD D、△EFC

查看试题解析

二、填空题（共6小题，每小题5分，共30分）

11. 平方根等于它本身的数是．

查看试题解析
12. 因式分解：16（x+y）²-（x-y）²＝．

查看试题解析
13. 从正三角形、正方形、正五边形、圆这四个图形中随机选出一个图形，结果是中心对称图形的概率为.

查看试题解析
14. 某商品随季节变化降价出售，如果按标价降价10%，仍可盈利40元．如果降价后再九折出售，就要亏损14元，则这件商品的标价是元．

查看试题解析
15. 如图，在菱形ABCD中，已知AB＝4，∠B＝60°，以AC为直径的⊙O与菱形ABCD相交，则图中阴影部分的面积为．

查看试题解析
16. 如图，点A，B，C，D是菱形的四个顶点，其中点A，D在反比例函数 $y = \frac{m}{x}$ （m＞0，x＞0）的图象上，点B，C在反比例函数 $y = \frac{n}{x} (n ＜ 0)$ 的图象上，且点B，C关于原点成中心对称，点A，C的横坐标相等，则 $\frac{m}{n}$ 的值为；过点A作AE∥x轴交反比例函数 $y = \frac{n}{x} (n ＜ 0)$ 的图象于点E，连结ED并延长交x轴于点F，连结OD．若S_△_DOF＝14，则m的值为．

查看试题解析

三、解答题（共8题，共80分）

17.

(1)、计算：2022⁰+（ $\frac{1}{3}$ ）^-¹+2sin60°-|3|．

(2)、解不等式组： ${\begin{array}{l} x + 2 > - 4 \\ 2 x - 3 < 5 \end{array}$

查看试题解析
18. 如图，在4×4的方格中，点A，B，C为格点，利用无刻度的直尺画出满足以下条件的图形（保留必要的辅助线）．

(1)、在图1中画△ABC的中线BE．

(2)、在图2中标注△ABC的外心O并画出其外接圆的切线CP．

查看试题解析
19. 端午节是我们中华民族的传统节日，某校九年级1班准备在端午节当天组织学生包粽子．班级分为男生（甲）女生（乙）两个小组，甲组男生在包粽子过程中因体育锻炼暂停一会，然后以原来的工作效率继续包粽子，由于时间紧任务重，乙组女生也加入共同加工粽子．设甲组男生加工时间t（分钟），甲组加工粽子的数量为y_甲（个），乙组女生加工粽子的数量为y_乙（个），其函数图象如图所示．

(1)、求y_乙与t之间的函数关系式，并写出t的取值范围；

(2)、求a的值，并说明a的实际意义；

(3)、甲组男生加工多长时间时，甲、乙两组加工粽子的总数为480个？

查看试题解析

20. 某校为庆祝国庆，组织全校学生参加党史知识竞赛，从中抽取200名学生的成绩（得分取正整数，满分100分）进行统计，绘制了如图尚不完整的统计图表．

200名学生党史知识竞赛成绩的频数表

组别（分）	频数	频率
50.5～60.5	10	0.05
60.5～70.5	a	0.10
70.5～80.5	26	0.13
80.5～90.5	b	0.40
90.5～100.5	64	c

请结合表中所给的信息回答下列问题：

(1)、频数表中，a＝， b＝， c＝；

(2)、将频数分布直方图补充完整；

(3)、若该校共有1500名学生，请估计本次党史知识竞赛成绩超过80分的学生人数．

查看试题解析

21. 如图1是可调节高度和桌面角度的电脑桌，它的左视图可以抽象成如图2所示的图形，底座AB长为60cm，支架CD垂直平分AB，桌面EF的中点D固定在支架CD处，EF宽为60cm．身高为160cm的使用者MN站立处点M与点A，B在同一条直线上，MA＝20cm．点N到点F的距离是视线距离．

(1)、如图2，当EF∥AB，CD＝100cm时，求视线距离NF的长；

(2)、如图3，使用者坐下时，高度MN下降50cm，当桌面EF与CD的夹角∠CDE为35°时，恰有视线NF∥AB，问需要将支架CD调整到多少cm？
（参考数据：sin35°≈0.43，cos35°≈0.90，tan35°≈0.47）

查看试题解析

22. 某城市发生疫情，第x天（1≤x≤15）新增病例y（人）如下表所示：

x	1	2	3	4	…	11	…
y	2	11	22	35	…	182	…

(1)、疫情前15天的人数模型基本符合二次函数y＝ax²+bx+c．根据图表，求出二次函数解析式．

(2)、由于疫情传染性强，第15天开始新增病例人数模型发生变化，第x天（x≥15）新增病例y（人）近似满足y＝-5（x-m）（x-13）．请预计第几天新增病例清零．

(3)、在（2）的条件下，为应对本轮疫情，按照每一确诊病例需当天提供一张病床的要求，政府应该在哪一天提供的病床最多？最多应该提供多少张？

查看试题解析

23. 定义：有两个相邻内角和等于另两个内角和的一半的四边形称为对半四边形，这两个角的夹边称为对半线．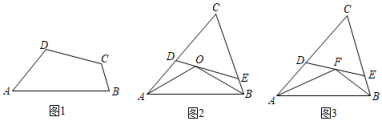

(1)、如图1，在对半四边形ABCD中，∠A+∠B＝ $\frac{1}{2}$ （∠C+∠D），求∠A与∠B的度数之和；

(2)、如图2，O为锐角△ABC的外心，过点O的直线交AC，BC于点D，E，∠OAB＝30°，求证：四边形ABED是对半四边形；

(3)、如图3，在△ABC中，D，E分别是AC，BC上一点，CD＝CE＝3，CE＝3EB，F为DE的中点，∠AFB＝120°，当AB为对半四边形ABED的对半线时，求AC的长．

查看试题解析
24. 如图1，△ABC内接于圆，点D在劣弧 $\overset{⌢}{AC}$ 上，AD＝ $\frac{1}{2}$ BC，DC＝ $\frac{1}{2}$ AB，Q为AC中点，点D与点P关于点Q对称.

(1)、求证：△PAD∽△ABC.

(2)、求证：点B，P，D在一条直线上.

(3)、如图2，记∠PAB＝α，∠PCB＝β，∠ABC＝θ，请用含α，β的代数式表示θ.

(4)、如图3，设E，F分别为AB，BC的中点，EF交BD于点H，求 $\frac{P H}{A C}$ 的值.

查看试题解析