陕西省渭南市蒲城县2022-2023学年七年级下学期期中数学试卷
试卷更新日期:2023-05-31 类型:期中考试
一、单选题
-
1. 芝麻被称为“八谷之冠”,是世界上最古老的油料作物之一,它作为食品和药物,得到广泛的使用.经测算,一粒芝麻的质量约为0.00000201千克,将0.00000201用科学记数法表示为( )A、 B、 C、 D、2. 如图,直线a、b、c被直线与直线所截,与是同位角关系的角有( )
 A、1个 B、2个 C、3个 D、4个3. 如图,笔直小路的一侧栽种有两棵小树 , , 小明测得 , , 则点到的距离可能为( )
A、1个 B、2个 C、3个 D、4个3. 如图,笔直小路的一侧栽种有两棵小树 , , 小明测得 , , 则点到的距离可能为( ) A、6m B、5m C、4m D、3m4. 计算的结果是( )A、 B、 C、 D、5. 有一个长为10,宽为6的长方形,若将长方形的宽增加 , 长不变,则增加的长方形的面积y与x之间的关系式为( )A、 B、 C、 D、6. 如图,为判断一段纸带的两边a,b是否平行,小明在纸带两边a,b上分别取点A,B,并连接AB.下列条件中,能得到的是( )
A、6m B、5m C、4m D、3m4. 计算的结果是( )A、 B、 C、 D、5. 有一个长为10,宽为6的长方形,若将长方形的宽增加 , 长不变,则增加的长方形的面积y与x之间的关系式为( )A、 B、 C、 D、6. 如图,为判断一段纸带的两边a,b是否平行,小明在纸带两边a,b上分别取点A,B,并连接AB.下列条件中,能得到的是( ) A、 B、 C、 D、7. 已知 , 则的值为( )A、201 B、210 C、402 D、4208. 小苏和小林在如图1所示的跑道上进行米折返跑.在整个过程中,跑步者距起跑线的距离y(单位:)与跑步时间t(单位:)的对应关系如图2所示.下列说法正确的是( )
A、 B、 C、 D、7. 已知 , 则的值为( )A、201 B、210 C、402 D、4208. 小苏和小林在如图1所示的跑道上进行米折返跑.在整个过程中,跑步者距起跑线的距离y(单位:)与跑步时间t(单位:)的对应关系如图2所示.下列说法正确的是( ) A、两人从起跑线同时出发,同时到达终点 B、小苏跑全程的平均速度大于小林跑全程的平均速度 C、小苏在跑最后的过程中,与小林相遇1次 D、小苏前跑过的路程大于小林前跑过的路程
A、两人从起跑线同时出发,同时到达终点 B、小苏跑全程的平均速度大于小林跑全程的平均速度 C、小苏在跑最后的过程中,与小林相遇1次 D、小苏前跑过的路程大于小林前跑过的路程二、填空题
-
9. 已知 , , 则 .10. 如图,某污水处理厂要从A处把处理过的水引入排水渠 , 为了节约用料,铺设垂直于排水渠的管道 . 这种铺设方法蕴含的数学原理是 .
 11. 如图,已知直线和相交于点O, , 平分 , , 则的度数为 .
11. 如图,已知直线和相交于点O, , 平分 , , 则的度数为 . 12. 某影剧院观众席的座位数按下列方式设置:
12. 某影剧院观众席的座位数按下列方式设置:排数(x)
1
2
3
4
……
座位数(y)
30
33
36
39
……
根据表格中两个变量之间的关系,当时,座位数 .
13. 如图,点D,E,F分别为三角形的边上的点,连接 , 作于点G.若 , , , 则的度数为°.
三、解答题
-
14. 计算:15. 如图,输入x,按如图所示的程序进行计算后,请用含x的代数式表示输出的结果.
 16. 已知与互余,若 , 求的补角的度数.17. 如图,点C,O在直线上,是一条射线,利用尺规作 , 使得 . (不写作法,保留作图痕迹)
16. 已知与互余,若 , 求的补角的度数.17. 如图,点C,O在直线上,是一条射线,利用尺规作 , 使得 . (不写作法,保留作图痕迹) 18. 如图,点D在三角形的边上,交于点F,若 , 试说明 .
18. 如图,点D在三角形的边上,交于点F,若 , 试说明 . 19. 下面的图象记录了某池塘一年中值的变化情况,请你仔细观察图象后回答下面的问题:
19. 下面的图象记录了某池塘一年中值的变化情况,请你仔细观察图象后回答下面的问题: (1)、5月份的值大约是;(2)、该池塘值最低的月份和最高的月份分别是几月?(3)、请简要描述4月到7月该池塘值的变化情况20. 先化简,再求值: , 其中 , .21. 如图,在梯形中, , , 高 , 点P为边上的动点,连接 , 当的长度由小到大变化时,四边形的面积也随之发生变化.
(1)、5月份的值大约是;(2)、该池塘值最低的月份和最高的月份分别是几月?(3)、请简要描述4月到7月该池塘值的变化情况20. 先化简,再求值: , 其中 , .21. 如图,在梯形中, , , 高 , 点P为边上的动点,连接 , 当的长度由小到大变化时,四边形的面积也随之发生变化. (1)、若设 , 四边形的面积为y,求y与x之间的关系式;(2)、当时,求四边形的面积.22. 如图,已知直线与交于点 , 与交于点 , 平分 , 若 , .
(1)、若设 , 四边形的面积为y,求y与x之间的关系式;(2)、当时,求四边形的面积.22. 如图,已知直线与交于点 , 与交于点 , 平分 , 若 , . (1)、求的度数;(2)、求的度数.23. 某种植基地有一块长方形实验田和一块正方形实验田,长方形实验田每排种植株豌豆幼苗,种植了排,正方形实验田每排种植株豌豆幼苗,种植了排,其中 .(1)、长方形实验田比正方形实验田多种植多少株豌豆幼苗?(2)、当 , 时,长方形实验田比正方形实验田多种植多少株豌豆幼苗?24. 王师傅非常喜欢自驾游,他为了了解新买轿车的耗油情况,将油箱加满后进行了耗油试验,得到下表中的数据:
(1)、求的度数;(2)、求的度数.23. 某种植基地有一块长方形实验田和一块正方形实验田,长方形实验田每排种植株豌豆幼苗,种植了排,正方形实验田每排种植株豌豆幼苗,种植了排,其中 .(1)、长方形实验田比正方形实验田多种植多少株豌豆幼苗?(2)、当 , 时,长方形实验田比正方形实验田多种植多少株豌豆幼苗?24. 王师傅非常喜欢自驾游,他为了了解新买轿车的耗油情况,将油箱加满后进行了耗油试验,得到下表中的数据:行驶的路程
0
100
200
300
400
……
油箱剩余油量
50
42
34
26
18
……
(1)、上表反映了哪两个变量之间的关系?哪个是自变量?哪个是因变量?(2)、这辆轿车油箱的容量是多少?当轿车行驶时,估计油箱中的剩余油量是多少?(3)、王师傅将油箱加满后驾驶该轿车从A地前往B地,到达B地时油箱中的剩余油量为 , 请求出A,B两地之间的路程.25. 如图,将一个长为、宽为的大长方形(如图1)剪成两个长分别为a和b、宽均为的小长方形,然后将这两个小长方形拼成如图2所示的图形,发现空白部分恰好是边长为a的正方形剪去边长为b的小正方形(阴影部分). (1)、图1中大长方形的面积可以表示为 , 图2中空白部分的面积可以表示为;(2)、根据(1)中的结果可以得到乘法公式: ▲ , 利用这个公式计算:
(1)、图1中大长方形的面积可以表示为 , 图2中空白部分的面积可以表示为;(2)、根据(1)中的结果可以得到乘法公式: ▲ , 利用这个公式计算:①;
②
26. 【问题提出】如图,在三角形中,D是上一点交于点E,F是线段延长线上的一点,连接 , 且。
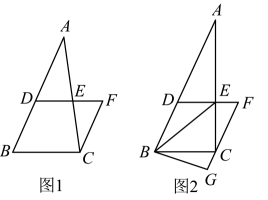 (1)、如图1,试说明;(2)、 【问题探究】
(1)、如图1,试说明;(2)、 【问题探究】如图2,连接 , 若:
①求的度数;
②点G是延长线上的一点,若 , 求的度数.