陕西省宝鸡市凤翔区2022-2023学年八年级下学期期中数学试卷

试卷更新日期：2023-05-31 类型：期中考试

进入出卷网下载

一、单选题

1. 下面说法错误的是（）

A、点 $(0 ， - 2)$ 在 $y$ 轴的负半轴上 B、点 $(3 ， 2)$ 与 $(3 ， - 2)$ 关于 $x$ 轴对称 C、点 $(- 4 ， - 3)$ 关于原点的对称点是 $(4 ， 3)$ D、点 $(- \sqrt{2} ， - \sqrt{3})$ 在第二象限

查看试题解析
2. 下列图形中，是轴对称图形但不是中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
3. 式子①x-y=2，②x $\leq$ y，③x+y，④x $^{2}$ -3y，⑤ x≥0，⑥ $\frac{1}{2}$ x $\neq$ 3中，属于不等式的有（）

A、2个 B、3个 C、4个 D、5个

查看试题解析
4. 如图，长为16cm的橡皮筋放置在x轴上，固定两端A和B，然后把中点C向上拉升6cm 至D点，则橡皮筋被拉长了（）

A、6cm B、5cm C、4cm D、2cm

查看试题解析
5. 不等式组 ${\begin{array}{l} x > - 3 \\ x < 5 \end{array}$ 的解集是（）

A、 $x > - 3$ B、 $x < 5$ C、 $- 3 < x < 5$ D、无解

查看试题解析
6. 如图，在直角三角尺ABC中，∠A=60°，过直角顶点C的直线MN和过点A的直线EF互相平行．若AB平分∠CAF，则∠1的大小是（）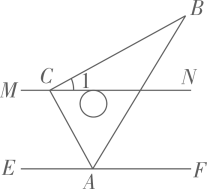

A、60° B、50° C、40° D、30°

查看试题解析
7. 已知点 $A (3 - m ， m - 1)$ 在第二象限，则 $m$ 的取值范围是（）

A、 $m > 3$ B、 $m < 1$ C、 $1 < m < 3$ D、无解

查看试题解析
8. 若一次函数 $y = 3 x + 6$ 与 $y = 2 x - 4$ 的图象的交点坐标为 $(a ， b)$ ，则解为 ${\begin{array}{l} x = a ， \\ y = b \end{array}$ 的方程组是（）

A、 ${\begin{array}{l} y - 3 x = 6 ， \\ 2 x + y = - 4 \end{array}$ B、 ${\begin{array}{l} 3 x + 6 + y = 0 ， \\ 2 x - 4 - y = 0 \end{array}$ C、 ${\begin{array}{l} 3 x - y + 6 = 0 ， \\ 2 x - y - 4 = 0 \end{array}$ D、 ${\begin{array}{l} 3 x - y = 6 ， \\ 2 x - y = 4 \end{array}$

查看试题解析
9. 铁路部门规定旅客免费携带行李箱的长、宽、高之和不超过160 cm，某厂家生产符合该规定的行李箱，已知行李箱的高为30 cm，长与宽的比为3∶2，则该行李箱的长的最大值为（）

A、30 cm B、160 cm C、26 cm D、78 cm

查看试题解析
10. 如图所示，在平面直角坐标系中 $A (0 ， 0)$ ， $B (4 ， 0)$ ， $△ A P_{1} B$ 是直角三角形，且 $∠ P_{1} = 90 °$ ， $∠ P_{1} B A = 30 °$ ， $P_{1}$ 到 $x$ 轴距离为 $\sqrt{3}$ ，把 $△ A P_{1} B$ 绕点 $B$ 顺时针旋转 $180 °$ ，得到 $△ B P_{2} C$ ；把 $△ B P_{2} C$ 绕点 $C$ 顺时针旋转 $180 °$ ，得到 $△ C P_{3} D$ ．依此类推，则旋转第2021次后，得到的直角三角形的直角顶点 $P_{2022}$ 的坐标为（）

A、 $(16167 ， \sqrt{3})$ B、 $(8087 ， - \sqrt{3})$ C、 $(8087 ， \sqrt{3})$ D、 $(16151 ， - \sqrt{3})$

查看试题解析

二、填空题

11. 同一平面上，两个等边三角形组成的各种图案，最多有条对称轴．

查看试题解析
12. 已知：点 $A (- 2022 ， - 1)$ 与点 $B (a ， b)$ 关于原点O成中心对称，则a+b= ．

查看试题解析
13. 不等式 $5 x + 1$ ≥ $3 x - 5$ 的解集为．

查看试题解析
14. 如图，点 $P$ 在 $∠ A O B$ 内，因为 $P M ⊥ O A$ ， $P N ⊥ O B$ ，垂足分别是 $M$ 、 $N$ ， $P M = P N$ ，所以 $O P$ 平分 $∠ A O B$ ，理由是．

查看试题解析
15. 如图，在△ABC中，AB＝6，AC＝9，EF垂直平分线段BC，P是直线EF上的任意一点，则△ABP周长的最小值是．

查看试题解析

三、解答题

16. 解不等式 $\frac{x - 2}{2} \leq \frac{7 - x}{3}$ ，并求出它的非负整数解．

查看试题解析
17. 解方程组： ${\begin{array}{l} 2 x - y = 8 ① \\ 3 x + 2 y = 5 ② \end{array}$

查看试题解析
18. 解不等式组： ${\begin{array}{l} 1 - x > 0 \\ \frac{5 x + 1}{2} \geq 2 x - 1 \end{array}$ ，并把解集表示在数轴上．

查看试题解析
19. 如图，已知线段c，求作等腰直角三角形，使其斜边等于线段c（保留作图痕迹，不必写作法）

查看试题解析
20. 如图，在 $△ A B C$ 中， $C D$ 是高， $B C = 7$ ， $B D = 6$ ．若 $D E ∥ B C$ ， $∠ D E C = ∠ D C B$ ，求 $C E$ 的长．

查看试题解析
21. 如图，在 $△ A B C$ 中， $∠ C = 90 ° ， ∠ A = 30 ° ， A B$ 的垂直平分线分别交 $A B ， A C$ 于点D，E.求证： $A E = 2 C E$ .

查看试题解析
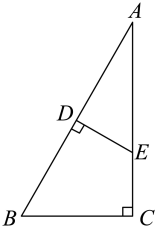22. 如图，下列 $4 \times 4$ 网格图都是由 $16$ 个相同小正方形组成，每个网格图中有 $4$ 个小正方形已涂上阴影，按下列要求涂上阴影.

(1)、在(图1)中选取2个空白小正方形涂上阴影，使6个阴影小正方形组成一个中心对称图形；

(2)、在(图2)中选取2个空白小正方形涂上阴影，使6个阴影小正方形组成一中心对称图形.(请将两个小题依次作答在图1，图2中，均只需画出符合条件的一种情形)

查看试题解析
23. 学校组织暑期夏令营，学校联系了报价均为每人200元的两家旅行社，经协商，甲旅行社的优惠条件是：全部师生 $7.5$ 折优惠；乙旅行社的优惠条件是：可免去一位老师的费用，其余师生8折优惠．

(1)、分别写出两家旅行社所需的费用y（元）与师生人数x（人）的函数关系式；

(2)、当师生人数是多少时，甲旅行社比乙旅行社更便宜．

查看试题解析
24. 如图，方格纸中每个小正方形的边长都是1，建立平面直角坐标系xOy，已知 $△ A B C$ 的三个顶点的坐标分别为A（－2，0），B（－1，－3），C（－3，－1）．

(1)、以原点为对称中心画出与△ABC成中心对称的图形，其中A，B，C的对应点分别为 $A_{1}$ ， $B_{1}$ ， $C_{1}$ ，写出点 $B_{1}$ ， $C_{1}$ 的坐标；

(2)、在（1）的条件下，点P在x轴上，连接 $P B_{1}$ ， $P C_{1}$ ，当 $P B_{1} + P C_{1}$ 取得最小值时，求此时点P的坐标．

查看试题解析
25. 如图，在△ABC中，AB=AC=2，∠B=40°，点D在线段BC上运动（D不与B、C重合），连接AD，作∠ADE=40°，DE交线段AC于E.

(1)、当∠BDA=115°时，∠BAD=°；点D从B向C运动时，∠BDA逐渐变（填“大”或“小”）；

(2)、当DC等于多少时，△ABD≌△DCE，请说明理由；

(3)、在点D的运动过程中，△ADE的形状也在改变，判断当∠BDA等于多少度时，△ADE是等腰三角形.

查看试题解析