陕西省宝鸡市陈仓区2022-2023学年八年级下学期期中质量检测数学试题
试卷更新日期：2023-05-31 类型：期中考试
一、单选题
-
1. 下列关于防范“新冠肺炎”的标志中既是轴对称图形，又是中心对称图形的是（ ）A、
戴口罩讲卫生
B、
勤洗手勤通风
C、
有症状早就医
D、
少出门少聚集
2. 若 ，则下列不等式成立的是（ ）A、 B、 C、 D、3. 用反证法证明“三角形中至少有一个内角大于或等于60°”时，应假设（ ）A、三角形的二个内角小于60° B、三角形的三个内角都小于60° C、三角形的二个内角大于60° D、三角形的三个内角都大于60°4. 如图，直线y=kx+b（k≠0）经过点A（﹣2，4），则不等式kx+b＞4的解集为（ ）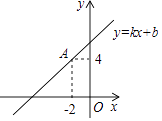
A、x＞﹣2 B、x＜﹣2 C、x＞4 D、x＜45. 如图，在 中， 的垂直平分线交 于点D， 平分 ，若 ，则 的度数为（ ）
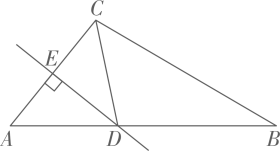A、 B、 C、 D、6. 线段MN是由线段EF经过平移得到的，若点E(﹣1，3)的对应点M(2，5)，则点F(﹣3，﹣2)的对应点N的坐标是（ ）A、(﹣1，0) B、(﹣6，0) C、(0，﹣4) D、(0，0)7. 如图，在等腰△ABC中，∠A=120°，AB=4，则△ABC的面积为（ ）
A、 B、4 C、 D、8. 不等式组 的解集是x＞2，则m的取值范围是（ ）
A、m≤2 B、m≥2 C、m≤1 D、m＞1二、填空题
-
9. 不等式的非正整数解为 ．10. 等腰三角形的一个内角为70°，则这个等腰三角形的三个角的度数为 ．11. 小明用50元钱购买矿泉水和冰淇淋，每瓶矿泉水2元，每支冰淇淋6元，他买了6瓶矿泉水和若干支冰淇淋，则小明最多能买支冰淇淋.12. 如图，将△ABE向右平移2cm得到△DCF，如果△ABE的周长是16cm，那么四边形ABFD的周长是 ．
13. 如图，在 中， ， ， ，AD是 的平分线.若P，Q分别是AD和AC上的动点，则 的最小值是.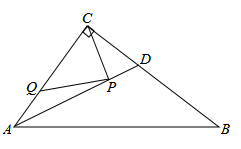
三、解答题
-
14. 如图，两公路与相交于点O，两公路内侧有两工厂C和D，现要修建一货站使货站P到两条公路OA、OB的距离相等，且到两工厂C、D的距离相等，用尺规作出货站P的位置．（要求：不写作法，保留作图痕迹）
15. 解不等式组 ， 并把解集在数轴上表示出来．16. 如图，△ABC中，AB=AC，D是BC的中点，E、F分别是AB、AC上的点，且AE=AF，求证：DE=DF．
17. 与在平面直角坐标系中的位置如图所示．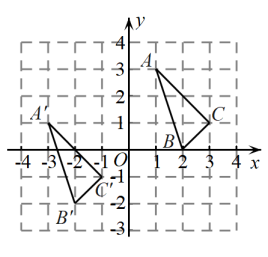
(1)、分别写出下列各点的坐标：A ， A'；(2)、若点是内部一点，则内部的对应点的坐标为；(3)、是由经过怎样的平移得到的？18. 某种商品的进价为900元，出售时标价为1650元，后来由于该商品积压，商店准备打折销售，但要保证利润率不低于10%，则最多可打几折？19. 如图，△ABC中，AB＝AC，DE是腰AB的垂直平分线．
(1)、若∠A＝40°，求∠DBC的度数；(2)、若AB＝9，BC＝5，求△BDC的周长．20. 如图，△ABC中，∠C=90°，∠A=30°，DE垂直平分线段AC．
(1)、求证：△BCE是等边三角形．(2)、若BC=3，求DE的长．21. 如图，在平面直角坐标系中，一次函数y=kx+b的图象与x轴交点为A（3，0），与y轴交点为B，且与正比例函数y=x的图象交于点C（m，4）．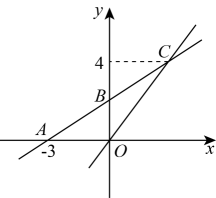
(1)、求m的值及一次函数y=kx+b的表达式；(2)、观察函数图象，直接写出关于x的不等式x＜kx+b的解集．22. 如图，△ABC是等边三角形，点D在AC边上，将△BCD绕点C旋转得到△ACE．
(1)、求证：DE∥BC；(2)、若AB＝8，BD＝7，求△ADE的周长．23. 如图，DE⊥AB于E，DF⊥AC于F，若BD=CD、BE=CF.
(1)、求证：AD平分∠BAC；(2)、已知AC=18， BE=4，求AB的长.24. 为增加校园绿化面积，某校计划购买甲、乙两种树苗．已知购买20棵甲种树苗和16棵乙种树苗共花费1280元，购买1棵甲种树苗比1棵乙种树苗多花费10元．(1)、求甲、乙两种树苗每棵的价格分别是多少元？(2)、若购买甲、乙两种树苗共100棵，且购买乙种树苗的数量不超过甲种树苗的3倍，则购买甲、乙两种树苗各多少棵时花费最少？请说明理由．25. 如图，两个等腰直角△ABC和△CDE中，∠ACB＝∠DCE＝90°．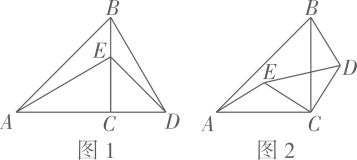
(1)、观察猜想如图1，点E在BC上，线段AE与BD的数量关系是 ， 位置关系是 ．(2)、探究证明把△CDE绕直角顶点C旋转到图2的位置，（1）中的结论还成立吗？说明理由；(3)、拓展延伸：把△CDE绕点C在平面内自由旋转，若AC＝BC＝13，DE＝10，当A、E、D三点在同一条直线上时，请直接写出AD的长．