黑龙江省齐齐哈尔市龙江县10校联考2022-2023学年九年级下学期期中数学试题
试卷更新日期:2023-05-31 类型:期中考试
一、单选题
-
1. 下列各数中,绝对值最大的数是( )A、 B、 C、 D、2. 下列图案中,不是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 3. 下列运算正确的是( )A、 B、 C、 D、4. 甲、乙、丙、丁四名运动员进行百米测试,每人8次测试成绩的平均数都是13.4秒,方差分别为 , , , , 则这四名运动员百米成绩最稳定的是( )A、甲 B、乙 C、丙 D、丁5. 一个几何体由若干个大小相同的小立方块搭成,如图分别是它的主视图和俯视图,若该几何体所用小立方块的个数为个,则的最小值为( )
3. 下列运算正确的是( )A、 B、 C、 D、4. 甲、乙、丙、丁四名运动员进行百米测试,每人8次测试成绩的平均数都是13.4秒,方差分别为 , , , , 则这四名运动员百米成绩最稳定的是( )A、甲 B、乙 C、丙 D、丁5. 一个几何体由若干个大小相同的小立方块搭成,如图分别是它的主视图和俯视图,若该几何体所用小立方块的个数为个,则的最小值为( )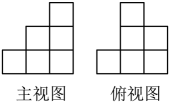 A、9 B、11 C、12 D、136. 从甲,乙,丙三人中任选两名代表,甲被选中的可能性是( )A、 B、 C、 D、7. 如图所示,在锐角中, , 分别是、边上的高,且与相交于点O,若 , 的度数为( )
A、9 B、11 C、12 D、136. 从甲,乙,丙三人中任选两名代表,甲被选中的可能性是( )A、 B、 C、 D、7. 如图所示,在锐角中, , 分别是、边上的高,且与相交于点O,若 , 的度数为( )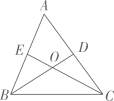 A、 B、 C、 D、8. 如图,已知直线是线段的中垂线,与相交于点C,D是位于直线下方的上的一动点(点D不与点C重合),连接 , 过点A作 , 过点B作于点E,若 , 设 , , 则y关于x的函数关系用图像可以大致表示为( ).
A、 B、 C、 D、8. 如图,已知直线是线段的中垂线,与相交于点C,D是位于直线下方的上的一动点(点D不与点C重合),连接 , 过点A作 , 过点B作于点E,若 , 设 , , 则y关于x的函数关系用图像可以大致表示为( ). A、
A、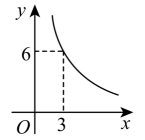 B、
B、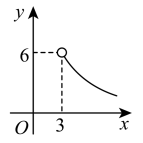 C、
C、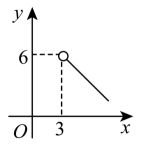 D、
D、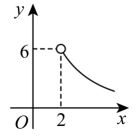 9. 学校计划购买A和B两种实验器材,已知A种器材每个60元,B种器材每个75元.学校准备将1500元钱全部用于购买这两种器材(两种都买),该学校的购买方案有( )A、3种 B、4种 C、5种 D、6种10. 如图,抛物线与x轴交于点 , 对称轴为 , 下列结论:①;②;③关于x的方程一定有两个不相等的实数根;④ . 其中结论正确的个数有( )
9. 学校计划购买A和B两种实验器材,已知A种器材每个60元,B种器材每个75元.学校准备将1500元钱全部用于购买这两种器材(两种都买),该学校的购买方案有( )A、3种 B、4种 C、5种 D、6种10. 如图,抛物线与x轴交于点 , 对称轴为 , 下列结论:①;②;③关于x的方程一定有两个不相等的实数根;④ . 其中结论正确的个数有( )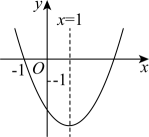 A、1个 B、2个 C、3个 D、4个
A、1个 B、2个 C、3个 D、4个二、填空题
-
11. 据中汽协会数据,年,由于海外供给不足和中国车企出口竞争力的大幅增强,汽车出口突破万辆,达到万辆,同比增长 , 中国已超过德国,成为全球第二大汽车出口国.万用科学记数法可表示为 .12. 如图,在平行四边形中,E,F是对角线上的两点,请添加一个条件 , 使四边形是平行四边形(填一个即可)
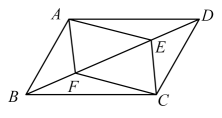 13. 如图,是圆锥底面的直径, , 母线 . 点为的中点,若一只蚂蚁从点处出发,沿圆锥的侧面爬行到点处,则蚂蚁爬行的最短路程为 .
13. 如图,是圆锥底面的直径, , 母线 . 点为的中点,若一只蚂蚁从点处出发,沿圆锥的侧面爬行到点处,则蚂蚁爬行的最短路程为 .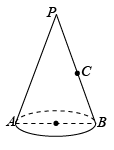 14. 已知关于x的方程=1的解是正数,则a的取值范围是 .15. 如图,在平面直角坐标系中,点是轴上任意一点,轴,分别交 , 的图象于两点,若的面积是 , 则的值为 .
14. 已知关于x的方程=1的解是正数,则a的取值范围是 .15. 如图,在平面直角坐标系中,点是轴上任意一点,轴,分别交 , 的图象于两点,若的面积是 , 则的值为 .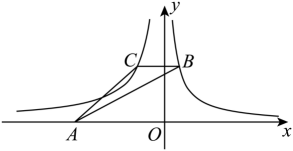 16. 已知在矩形中, , , P为上一点,连接 . 将沿折叠,点B的对应点是点G,连接 , 当为直角三角形时,的长为 .17. 如图,在平面直角坐标系中,点的坐标为 , 以为直角边作 , 使 , 再以为直角边作 , 使 , 再以为直角边作 , 使……按此规律进行下去,点的坐标是 .
16. 已知在矩形中, , , P为上一点,连接 . 将沿折叠,点B的对应点是点G,连接 , 当为直角三角形时,的长为 .17. 如图,在平面直角坐标系中,点的坐标为 , 以为直角边作 , 使 , 再以为直角边作 , 使 , 再以为直角边作 , 使……按此规律进行下去,点的坐标是 .
三、解答题
-
18. 按要求计算(1)、计算:(2)、因式分解: .19. 解方程: .20. 某市为了解初中生每周锻炼身体的时长(单位:小时)的情况,在全市随机抽取部分初中生进行调查,按五个组别:A组();B组();C组();D组();E组()进行整理,绘制成如下两幅不完整的统计图,根据图中提供的信息,解决下列问题:
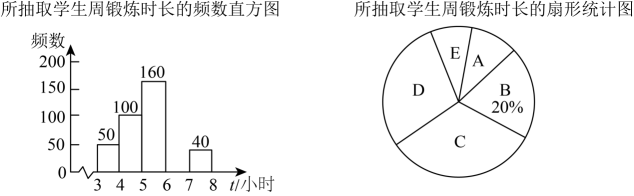 (1)、求出这次抽样调查的学生总人数;(2)、补全频数分布直方图;(3)、C组所在扇形的圆心角的度数为度;(4)、根据样本估计全市12000名初中生中,每周锻炼身体的时长不少于5小时的有多少名.21. 如图,已知是的外接圆,是的直径,是延长线上的一点,交的延长线于点 , 于点 , 且 .
(1)、求出这次抽样调查的学生总人数;(2)、补全频数分布直方图;(3)、C组所在扇形的圆心角的度数为度;(4)、根据样本估计全市12000名初中生中,每周锻炼身体的时长不少于5小时的有多少名.21. 如图,已知是的外接圆,是的直径,是延长线上的一点,交的延长线于点 , 于点 , 且 .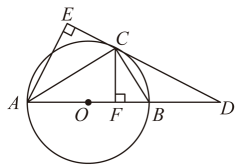 (1)、求证:是的切线;(2)、若 , , 求的长.22. 甲、乙、丙三地顺次在一条公路上,一辆客车和一辆货车分别在甲、丙两地同时出发,客车从甲地出发匀速驶往丙地,中途在乙地停留了2小时,然后以原速行驶到达丙地,货车从丙地出发匀速行驶,直接到达甲地.两车距离乙地的路程y(单位:千米)与行驶时间(单位:小时)之间的函数关系如图所示.
(1)、求证:是的切线;(2)、若 , , 求的长.22. 甲、乙、丙三地顺次在一条公路上,一辆客车和一辆货车分别在甲、丙两地同时出发,客车从甲地出发匀速驶往丙地,中途在乙地停留了2小时,然后以原速行驶到达丙地,货车从丙地出发匀速行驶,直接到达甲地.两车距离乙地的路程y(单位:千米)与行驶时间(单位:小时)之间的函数关系如图所示.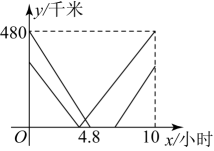 (1)、求出客车和货车的速度;(2)、求客车从甲地驶向丙地的过程中y与x之间的函数关系式;(3)、求两车在行驶途中何时相遇;(4)、直接写出两车在行驶途中何时相距100千米.23. 综合与实践如图,正方形与正方形有公共顶点C, , , 连接 .
(1)、求出客车和货车的速度;(2)、求客车从甲地驶向丙地的过程中y与x之间的函数关系式;(3)、求两车在行驶途中何时相遇;(4)、直接写出两车在行驶途中何时相距100千米.23. 综合与实践如图,正方形与正方形有公共顶点C, , , 连接 .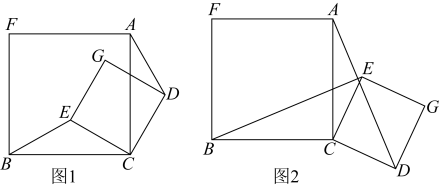 (1)、如图①,当点E,G在正方形内时,线段与的数量关系是 , 位置关系是;(2)、把正方形绕点C旋转到如图②的位置,(1)中的结论还成立吗?说明理由;(3)、把正方形绕点C在平面内自由旋转.
(1)、如图①,当点E,G在正方形内时,线段与的数量关系是 , 位置关系是;(2)、把正方形绕点C旋转到如图②的位置,(1)中的结论还成立吗?说明理由;(3)、把正方形绕点C在平面内自由旋转.①当A,E,D三点在同一条直线上时,AE的长是;
②旋转过程中,的最大值为 .
24. 综合与探究如图,抛物线与轴交于点A、点B,与y轴交于点C,直线与抛物线交于点B、点C,直线与抛物线交于点A,与y轴交于点E,与直线交于点F.
 (1)、求抛物线的解析式;(2)、已知点在抛物线上,当时,直接写出的取值范围;(3)、H是直线CB上一点,若 , 求点H的坐标;(4)、P是轴上一点,Q是平面内任意一点,是否存在以B,C,P,Q为顶点的四边形是菱形?者存在,请直接写出点Q的坐标;若不存在,请说明理由.
(1)、求抛物线的解析式;(2)、已知点在抛物线上,当时,直接写出的取值范围;(3)、H是直线CB上一点,若 , 求点H的坐标;(4)、P是轴上一点,Q是平面内任意一点,是否存在以B,C,P,Q为顶点的四边形是菱形?者存在,请直接写出点Q的坐标;若不存在,请说明理由.